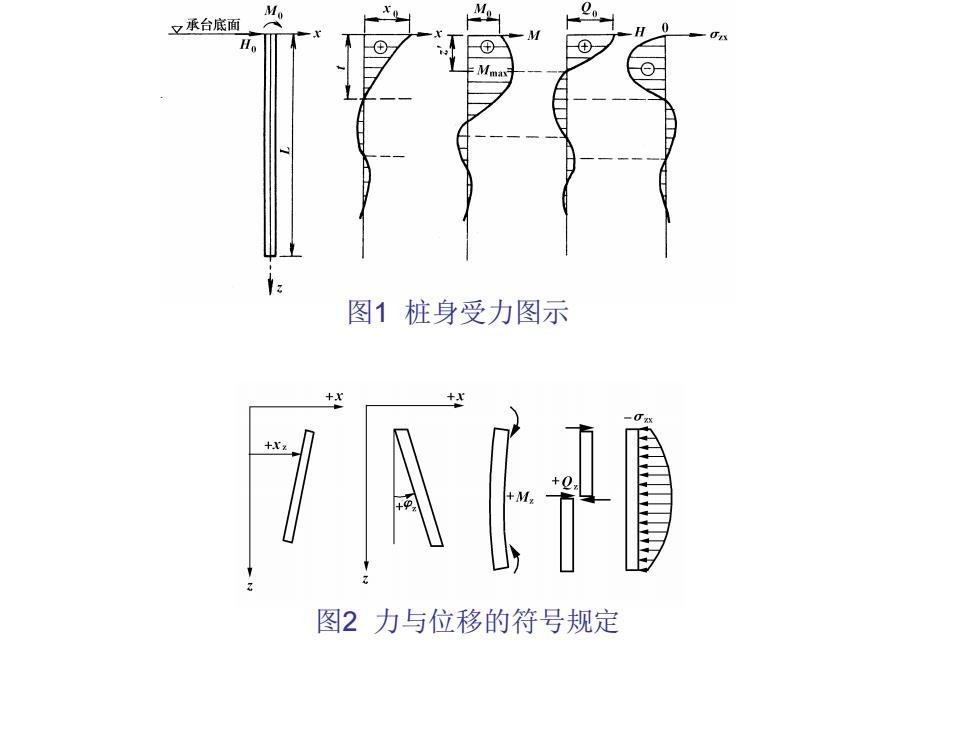
又承台底面 图1桩身受力图示 图2力与位移的符号规定
图1 桩身受力图示 图2 力与位移的符号规定

(一)桩的挠曲微分方程的建立及其解 桩顶若与地面平齐(Z=0),且已知桩顶作用有水平 荷载Qo及弯矩Mo,此时桩将发生弹性挠曲,桩侧土将产 生横向抗力ox,如图1所示。从材料力学中知道,梁轴 的挠度与梁上分布荷载q之间的关系式,即梁的挠曲微分 方程为 El 14x 式中:E、一梁的弹性模量及截面惯矩。 因此可以得到图1所示桩的挠曲微分方程为 =-g=-osb=-mZx:b d24
(一)桩的挠曲微分方程的建立及其解 桩顶若与地面平齐(Z=0),且已知桩顶作用有水平 荷载Q0及弯矩M0,此时桩将发生弹性挠曲,桩侧土将产 生横向抗力zx,如图1所示。从材料力学中知道,梁轴 的挠度与梁上分布荷载q之间的关系式,即梁的挠曲微分 方程为 q dZ d x EI = − 4 4 式中:E、I——梁的弹性模量及截面惯矩。 因此可以得到图1所示桩的挠曲微分方程为 4 1 1 4 q b mZx b d Z d x EI z x z z = − = − = −

上式中:E、一桩的弹性模量及截面惯矩 02x—桩侧土抗力ozx=Cxz=m2X2, C为地基系数; b1一桩的计算宽度; X2—一桩在深度z处的横向位移(即桩的挠度)。 dx. 将上式整理可得: d24 mbL Zx.=0 (1) EI 或 d4x+a2z:=0 d24 5 式中:o一桩一土变形系数,0=1 EI 从上式中不难看出:桩的横向位移与截面所在深度、 桩的刚度(包括桩身材料和截面尺寸)以及桩周土的性质 等有关,o是与桩土变形相关的系数
上式中:E、I——桩的弹性模量及截面惯矩 zx——桩侧土抗力zx=Cxz=mZxz,C为地基系数; b1——桩的计算宽度; xz——桩在深度z处的横向位移(即桩的挠度)。 将上式整理可得: 或 0 1 4 4 + z = z Zx EI mb dZ d x 0 5 4 4 + z = z a Zx dZ d x 式中:——桩—土变形系数, 5 1 EI mb = 从上式中不难看出:桩的横向位移与截面所在深度、 桩的刚度(包括桩身材料和截面尺寸)以及桩周土的性质 等有关,是与桩土变形相关的系数。 (1)

式(1)为四阶线性变系数齐次常微分方程,在求解 过程中注意运用材料力学中有关梁的挠度x,与转角2弯 矩M,和剪力Q,之间的关系即 dz M.=EI d=2 Q.=E1 若地面处(Z=0)桩的水平位移、转角、弯矩和剪力分 别以Xo、0、M和Q表示,解方程组(1),得到桩身任一 截面的转角pz、弯矩M2,及剪力Qz的计算公式:
式(1)为四阶线性变系数齐次常微分方程,在求解 过程中注意运用材料力学中有关梁的挠度xz与转角z、弯 矩Mz和剪力Qz之间的关系即 = = = 3 3 2 2 dz d x Q EI dz d x M EI dz dx z z z z z z 若地面处(Z=0)桩的水平位移、转角、弯矩和剪力分 别以x0、0、M0和Q0表示,解方程组(1),得到桩身任一 截面的转角Z、弯矩MZ,及剪力QZ的计算公式:

X-=X04+ 6B1+1 M0 2 EI C a El (2) =+B,+ Mo-C2+ a (3) -EI 2. =4+B, (4) aEl EI EI (5 A1、B1...C4、D4一16个无量纲系数,根据不同的无量纲 深度可将其制成表格供查用(参见《公桥基规》)。 根据土抗力的基本假定ox=CX,=mZX,,可求得桩侧土抗 力的计算公式: 2m=n2++g (6
1 3 0 1 2 0 1 0 0 1 D EI Q C EI M X z x A B = + + + 2 3 0 2 2 0 2 0 0 2 D EI Q C EI M x A B Z = + + + 3 4 0 2 4 0 4 0 3 0 4 D EI Q C EI M x A B EI QZ = + + + = = + + + 1 3 0 1 2 0 1 0 0 1 D EI Q C EI M z x mZX z mZ x A B (2) (3) (4) (5) A1、B1……C4、D4——16个无量纲系数,根据不同的无量纲 深度可将其制成表格供查用(参见《公桥基规》)。 根据土抗力的基本假定 zx = CX z = mZX z ,可求得桩侧土抗 力的计算公式: = = + + + 1 3 0 1 2 0 1 0 0 1 D EI Q C EI M z x mZX z mZ x A B (6)