
解(0)因为m0是宽平稳的随机过程,所以其均值为瓯m仞=(常数)而9 是服从均匀分布的,所以8)=2m,(0<8<2知),又因为8是与 m)彼此统计独立的,所以 ze】=ELmd)cos(am,t+a】= =B(m(ant cos0-sin ant sin =Emt)E[cos at cose-sin aot sin] =af"[cosatcos-sin sind0 R.)=[z64】=可m4)cos(a4+)m4)cos@+aJ Bli(t1yn(t2)Elcos aot1+e)cos(an2+e)] =0.5Rm(F)Ecoslao(1+ta)+20]+cos@o(t2-) =0.5R(tXElcosao(-1)]+Ecosa(+)cos20- m4+6)m20]} =0.5R(cos2-4】+0} =0.5R.tlcosot 令2-61=t) 由于R,)与时间起点无关,而职与时间间隔有关,且[e)=0与 时间无关,所以z)是宽平稳的。 0.5(1+)cosor -1<r<0 (2)R()-O.5R()cos@o- 0.51-r)c0so 0<x1 其他 R(:的波形可以看成一个余弦函数和一个三角波的乘积.如图2.所示 (3)因为z0是宽平稳的,所以,P()台Rz(t) B回-x6e+a,+o-ao58) 1Sa2(@+m)a2(@-m 2 2 8=R0= R()卡 12 图2.1
16
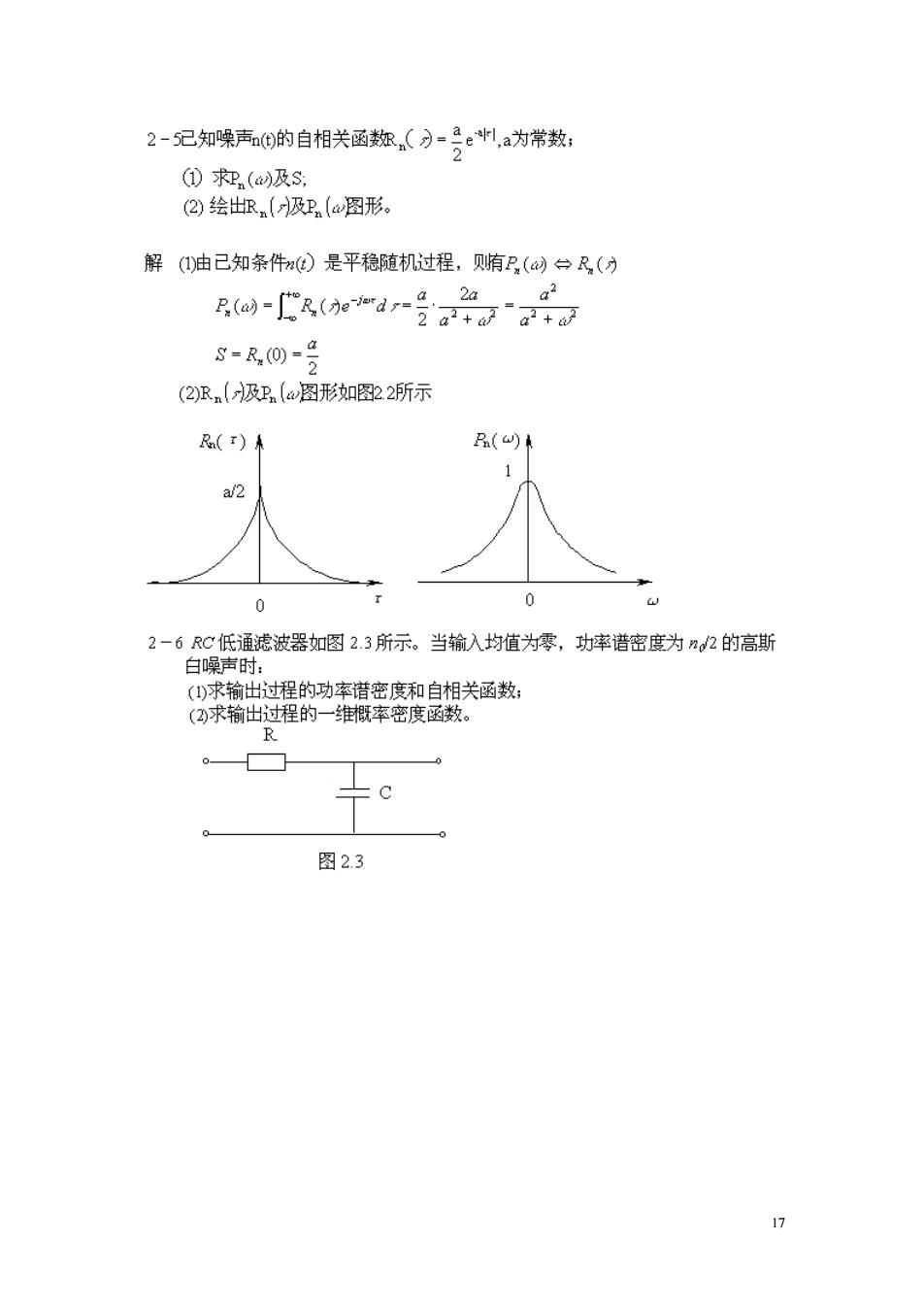
2-5记知噪声0的自相关函如,()-2e1,a为常数; (①求()及s, (②)绘出R(及Pn(图形 解()油已知条件:)是平稳随机过程,贿R()台R( Bo-(9d-受a”aad 2 8-R@-号 (2R.(汲卫.(a图形如图22所示 R(r)米 B()h a/2 T 0 2-6RC低通滤波器如图2.3所示。当输入均值为零,功率谱密度为n2的高斯 白噪声时: ()求输出过程的功率谱密度和自相关函数: (3求输出过程的一维相概率密度数。 R 。☐ 上c 0 图2.3
17

解 (H(e)-jac 1 aRc) 输出功率谱密度为 B(a)-lHo(- 2 1+(aRC) 因为R,(o一R利用e州一。 2a 自相关为( (2因为高斯过程通过线性系统后仍为高斯过程 而56)-5H(0)-=0 g2-R0-R=4 所以输出过程的一维概率密度函数为 x 2-7()是一个平稳随过程,它的自相关函数是周期为2:的周期函数。在区 间C 1,1)( ,该自相关函数R(t)=1-|r试求g()的功率 谱密度P(“,并用图形表示
18

解因为)是一个平稳随机过程,所以()台R() 对进行博里叶变换,得P@-侣) -=艺xado-)-立}a-a) 图形如图2.4所标 P:@) 4-2京024 图2.4 h家 rw) 218 -的,-双B-,-动,+万80的-T8的,品,卡石B
19

解ú)将高斯白唤声加到一个理想带通滤波器上,其输出是一个窄带高斯白噪 o-{)5@+d (o)-F(Y'p(o) 又因为R回)一R) 所以R,e)-}-Role-dm ·六C2学“o+法上学- =nB(Becos①,r 口图资需数程经过线乳系统后奶是感过程,所心喘出染声的一推帮幸 m高 因为版】=0 包 所以a 所以输出噪声的一维概率密度函数为 1 f同:m网2玩可 h() 0,(t) h0日 05,( 图2.6
20