
《通信原理》第十一章同步原理习题 第十一章同步原理习题 1.在插入导频法框图中,asinot不经过90'相移,直接与已调信号相加输出。试证明接收 端的解调输出中含有直流分量。 证明:发端: uft)=m(t)asinot+asinot 收端: v(t)=u(t)sinot=[m(t)asinwt+asinot]sinot=a [1+m(t)]sin?ot =1/2:a[1+m(t)1(1-cos20t) =1/2-a[1+m(t)]-1/2-a[1+m(t)1cos2wt 经低通滤波器后,滤除高频分量,输出为 v(t)=1/2a[1+m(t)1=1/2a+1/2am(t) 故解调器输出的信号有直流分量a/2。 2.已知单边带信号的表示为s(t)m(t)coswt+i(t)sinot,血(t)是m(t)的希尔伯特变 换,若采用与抑制载波双边带信号导频插入完全相同的方法,试证明接收端可正确解调:若 发端插入的导频是调制载波,试证明解调输出中也含有直流分量,并求出该值, 解:(1)v(t)Fu(t)sint=[s(t)-acoswt】sinot =[m(t)cosot+(t)sinot-acosot]sinot =1/2m(t)sin2ot+1/2(t)(1-cos2wt)-1/2a sin2wt =1/2 m(t)+1/2m(t)sin2wt-1/2a sin2ot-1/2 (t)cos20t 经低通滤波器,滤除高频分量,输出为 m'(t)=1/2i(t) 经90相移后,即可得到正确的解调信号。 120
《通信原理》第十一章 同步原理 习题 120 第十一章 同步原理 习题 1.在插入导频法框图中, ąsinωt 不经过 90˚相移,直接与已调信号相加输出。试证明接收 端的解调输出中含有直流分量。 证明:发端: u{t}=m(t)·ąsinωt+ąsinωt 收端: v(t)=u(t)sinωt=[ m(t)·ąsinωt+ąsinωt]sinωt=a[1+m(t)]sin²ωt =1/2·ą[1+m(t)](1-cos2ωt) =1/2·ą[1+m(t)]- 1/2·ą[1+m(t)] cos2ωt 经低通滤波器后,滤除高频分量,输出为 v(t)= 1/2·ą[1+m(t)]= 1/2·ą+1/2·ąm(t) 故解调器输出的信号有直流分量 ą/2。 2.已知单边带信号的表示为 s(t)=m(t)cosωt+ (t)sinωt, (t)是 m(t)的希尔伯特变 换,若采用与抑制载波双边带信号导频插入完全相同的方法,试证明接收端可正确解调;若 发端插入的导频是调制载波,试证明解调输出中也含有直流分量,并求出该值。 解:(1) v(t)=u(t)sinωt=[s(t)-ącosωt] sinωt =[m(t)cosωt+ (t)sinωt-ącosωt] sinωt =1/2m(t) sin2ωt+1/2 (t)(1-cos2ωt)-1/2ą sin2ωt =1/2 (t)+1/2m(t)sin2ωt-1/2ą sin2ωt-1/2 (t)cos2ωt 经低通滤波器,滤除高频分量,输出为 m’(t)=1/2 (t) 经 90º相移后,即可得到正确的解调信号
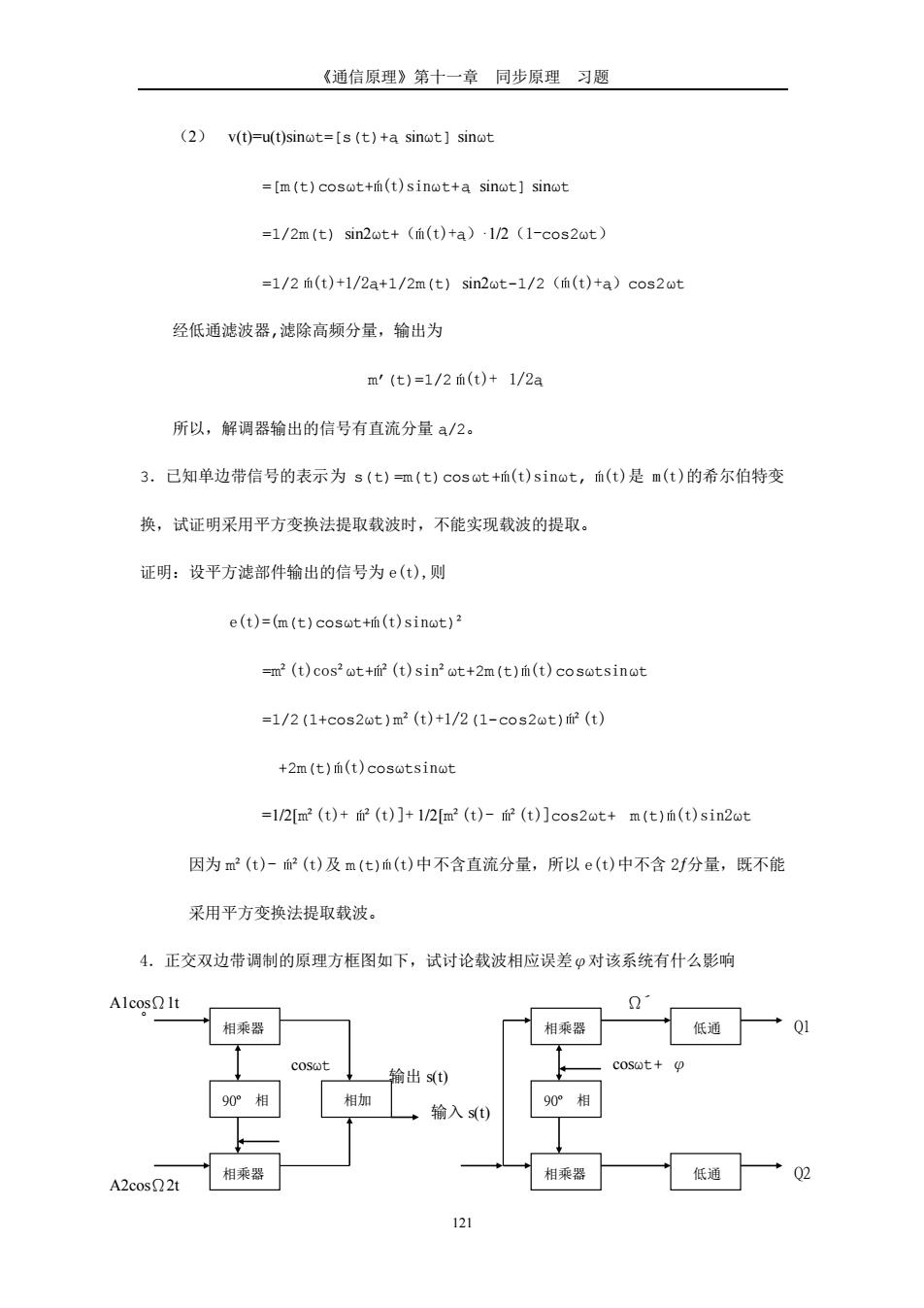
《通信原理》第十一章同步原理习题 (2)v(t)=u(t)sinot=[s(t)+a sinwt]sinot =[m(t)cost+i(t)sin公t+a sinot】sinot =1/2m(t)sin2ot+((t)ta)-I/2 (1-cos2ot) =1/2(t)+1/2a+1/2m(t)sin2wt-1/2(m(t)+a)cos2wt 经低通滤波器,滤除高频分量,输出为 m'(t)=1/2m(t)+1/2a 所以,解调器输出的信号有直流分量a/2。 3.已知单边带信号的表示为s(t)m(t)cost+(t)sinot,(t)是m(t)的希尔伯特变 换,试证明采用平方变换法提取载波时,不能实现载波的提取。 证明:设平方滤部件输出的信号为©(t),则 e(t)=(m(t)cosot+(t)sinot) -m(t)cos(t)sint+2m(t)(t)cosotsint =1/2(1+cos2ot)m2(t)+1/2(1-cos2ot)㎡(t) +2m(t)(t)cosotsinot =1/2[m(t)+(t)]+1/2[m(t)-(t)]cos2ot+m(t)(t)sin2t 因为m2(t)-(t)及m(t)血(t)中不含直流分量,所以e(t)中不含2f分量,既不能 采用平方变换法提取载波。 4.正交双边带调制的原理方框图如下,试讨论载波相应误差对该系统有什么影响 1 相乘器 相乘器 低通一Q 00相 相乘器 相乘器 低通厂 02 2c0s02
《通信原理》第十一章 同步原理 习题 121 (2) v(t)=u(t)sinωt=[s(t)+ą sinωt] sinωt =[m(t)cosωt+ (t)sinωt+ą sinωt] sinωt =1/2m(t) sin2ωt+( (t)+ą)·1/2(1-cos2ωt) =1/2 (t)+1/2ą+1/2m(t) sin2ωt-1/2( (t)+ą)cos2ωt 经低通滤波器,滤除高频分量,输出为 m’(t)=1/2 (t)+ 1/2ą 所以,解调器输出的信号有直流分量 ą/2。 3.已知单边带信号的表示为 s(t)=m(t)cosωt+ (t)sinωt, (t)是 m(t)的希尔伯特变 换,试证明采用平方变换法提取载波时,不能实现载波的提取。 证明:设平方滤部件输出的信号为 e(t),则 e(t)=(m(t)cosωt+ (t)sinωt)² =m²(t)cos²ωt+ ²(t)sin²ωt+2m(t) (t)cosωtsinωt =1/2(1+cos2ωt)m²(t)+1/2(1-cos2ωt) ²(t) +2m(t) (t)cosωtsinωt =1/2[m²(t)+ ²(t)]+ 1/2[m²(t)- ²(t)]cos2ωt+ m(t) (t)sin2ωt 因为 m²(t)- ²(t)及 m(t) (t)中不含直流分量,所以 e(t)中不含 2ƒ分量,既不能 采用平方变换法提取载波。 4.正交双边带调制的原理方框图如下,试讨论载波相应误差φ对该系统有什么影响 。 相乘器 90º 相 移 相乘器 相加 低通 低通 相乘器 相乘器 90º 相 移 A1cosΩ1t A2cosΩ2t 输出 s(t) 输入 s(t) Ω´ cosωt+ φ φ cosωt Q1 Q2

《通信原理》第十一章同步原理习题 解:st)=A1cos?1 t cosot+A2cosQ2 tsint 解调时,上支路: Q1 =s(t)cos(wt+) =(AlcosIt cot+A2cos2tsint)co) =Alcos It coswt cos)+A2cos2tsinot cos+) =1/2 Alcos It(cos2ot++cos)+1/2 A2cos2t(sin2t++sin) =1/2AlcosQ Itcos+1/2A2cosQ2t sin +1/2 AlcosItcos2ot++1/2 A2cos!2tsin2t+ 经低通滤波器,滤除高频分量,输出为 Ql=1/2 AlcosQItcos+1/2 A2cosQ2t sin 同理,可得 Q2=1/2AlcosQ Itsin+1/2 A2cosQ2t cos 以上支路为例,Q1中的有用信号为 1/2Alcos Itcos 与发端信号A1cos21t比较,多了一个因子cosp,它使有用信号功率降低,Q1中的第 二项为 1/2A2cosQ2tsin 由于它与有用信号无关,可理解为干扰。 综上所述,载波相应误差印对信号解调的影响主要有两方面,一是使有用信号功率降 低,二是使上·下两支路的信号互相干扰,即各支路信号发生泄漏,进入其它支路,对其它 支路信号形成干扰。 122
《通信原理》第十一章 同步原理 习题 122 解:s(t)=A1cosΩ1t cosωt+ A2cosΩ2tsinωt 解调时,上支路: Q1´=s(t)cos(ωt+φ) =( A1cosΩ1t cosωt+ A2cosΩ2tsinωt) cos(ωt+φ) = A1cosΩ1t cosωt cos(ωt+φ)+ A2cosΩ2tsinωt cos(ωt+φ) =1/2 A1cosΩ1t(cos2ωt+φ+cosφ)+1/2 A2cosΩ2t(sin2ωt+φ+sinφ) =1/2 A1cosΩ1tcosφ+1/2 A2cosΩ2t sinφ +1/2 A1cosΩ1tcos2ωt+φ+1/2 A2cosΩ2tsin2ωt+φ 经低通滤波器,滤除高频分量,输出为 Q1=1/2 A1cosΩ1tcosφ+1/2 A2cosΩ2t sinφ 同理,可得 Q2=1/2 A1cosΩ1tsinφ+1/2 A2cosΩ2t cosφ 以上支路为例,Q1 中的有用信号为 1/2 A1cosΩ1tcosφ 与发端信号 A1cosΩ1t 比较,多了一个因子 cosφ,它使有用信号功率降低,Q1 中的第 二项为 1/2 A2cosΩ2tsinφ 由于它与有用信号无关,可理解为干扰。 综上所述,载波相应误差φ对信号解调的影响主要有两方面,一是使有用信号功率降 低,二是使上、下两支路的信号互相干扰,即各支路信号发生泄漏,进入其它支路,对其它 支路信号形成干扰

《通信原理》第十一章同步原理习题 5.在插入导频法框图中,接收端信号不经过90相移,试证明接收端的解调输出中含有直流 分量。 证明:发端: ut)=m(t)asinwt-acoswt 收端: v(t)=u(t)cosot =m(t)asinot-acosot]cosot =1/2m(t)asin2wt-1/2a(1+cos2ot) =1/2m(t)asin2wt-1/2a-1/2acos2wt 经低通滤波器后,滤除高频分量,输出为 v(t)=-1/2a 故解调器输出的信号有直流分量a/2。 故解调器输出的信号有直流分量-4/2。 6.在插入导频法框图中,接收端的带通与∫窄带滤波器有何区别? 答:带通:滤除所需信号频谱以外的噪声频谱, ∫窄带滤波器:提取含f频谱的载波。 7.画插入导频法框图。 解 调制信号相乘调制】 一带通上 相如 输出 m(t) a(t) 找波源 一90相移 asinot 插入导频法发端框图 123
《通信原理》第十一章 同步原理 习题 123 5.在插入导频法框图中,接收端信号不经过 90˚相移,试证明接收端的解调输出中含有直流 分量。 证明:发端: u{t}=m(t)·ąsinωt-ącosωt 收端: v(t)=u(t)cosωt =[ m(t)·ąsinωt-ącosωt]cosωt =1/2m(t)·ąsin2ωt-1/2ą(1+cos2ωt) =1/2m(t)·ąsin2ωt-1/2ą-1/2ącos2ωt 经低通滤波器后,滤除高频分量,输出为 v(t)= -1/2ą 故解调器输出的信号有直流分量 ą/2。 故解调器输出的信号有直流分量-ą/2。 6. 在插入导频法框图中,接收端的带通与 ƒ 窄带滤波器有何区别? 答:带通:滤除所需信号频谱以外的噪声频谱。 ƒ 窄带滤波器:提取含 ƒ 频谱的载波。 7.画插入导频法框图。 解: 插入导频法发端框图 相乘调制 带通 相加 载波源 90˚相移 ąsinωt 调制信号 m(t) 输出 u(t)

《通信原理》第十一章同步原理习题 带通 相乘器 低通) /窄带滤波器 90相移 插入导频法收端框图 8.己知fm=980khz,f=100khz,△f1=10khz,△2=10khz,求经过几次分频? 解:按公式q=1+(fm+△1)fr+△2),计算得 q=10 所以经过10次分频。 9.画平方变换法提取载波框图。 输入已遇平方律部件©七)2f窄带滤波器 三分颜或泼验出 信号 平方变换法提取载波 10.画残留边带信号插入导频法收端框图 解: 收信号 相乘器 窄带上移相截波出一 残留边带信号插入导频法收端框图 124
《通信原理》第十一章 同步原理 习题 124 插入导频法收端框图 8.已知 ƒm=980khz, ƒr=100khz, Δƒ1=10khz, Δƒ2=10khz,求经过几次分频? 解:按公式 q=1+(ƒm+Δƒ1)/( ƒr+Δƒ2),计算得 q=10 所以经过 10 次分频。 9.画平方变换法提取载波框图。 平方变换法提取载波 10.画残留边带信号插入导频法收端框图。 解: 残留边带信号插入导频法收端框图 带通 ƒ 窄带滤波器 90˚相移 u(t) 相乘器 低通 m(t) v(t) 输入已调 平方律部件 2 ƒ 窄带滤波器 二分频 信号 e(t) 载波输出 输 ƒ1 窄带 ƒ2 窄带 相乘器 (ƒ2-ƒ1) 低通 q 次分频 相乘器 ƒ 窄带 移相 收信号 载波输出 输 l