调和平均数与算术均数的区别? (1) (2) 价格 销售量 价格 销售额 (元斤) (斤) (元斤) (元) 3.3 3 3.3 10 2.5 4 2.5 10 2.0 5 2.0 10 合计 12 合计 30 3 ∑对 3.3×3+2.5×4+2.0×5 3+4+5 =249元/斤 0+10+10 XH= 10 =2.49元/斤 ,10.10 3.32.52.0 26
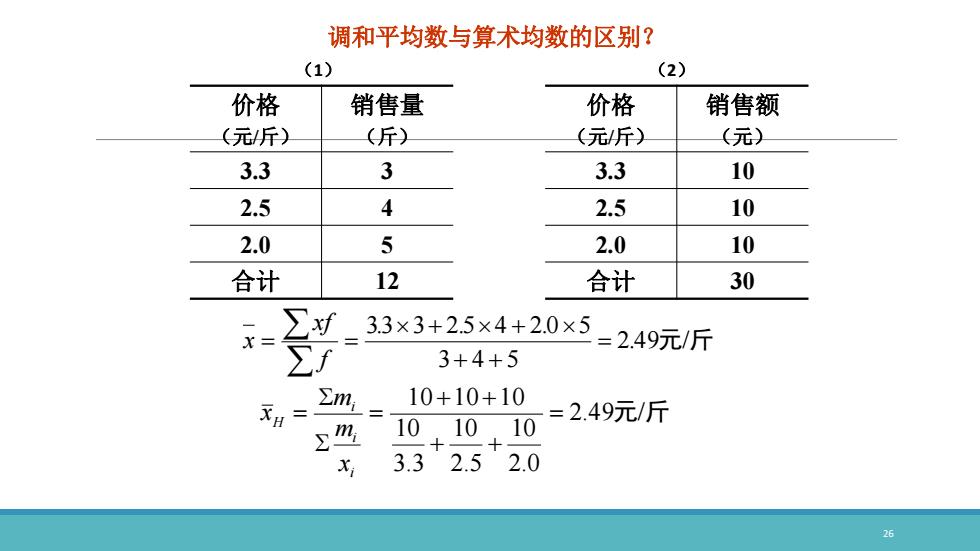
26 调和平均数与算术均数的区别? 价格 (元/斤) 销售量 (斤) 3.3 3 2.5 4 2.0 5 合计 12 价格 (元/斤) 销售额 (元) 3.3 10 2.5 10 2.0 10 合计 30 2.49元/斤 2.0 10 2.5 10 3.3 10 10 10 10 i i i H x m m x 2 4 9元/斤 3 4 5 33 3 2 5 4 2 0 5 . . . . f xf x (1) (2)

三、几何平均数 n个变量值乘积的n次方根就是几何平均数。 xc=Vx1Xx2X.Xx=V昭1x 几何平均数常用于计算合格率、发展速度、利率等变量的平均,因为这类比率的 变量,变量值的连乘积为总比率,不能用算术平均方法,只能用几何平均数计算平均 指标。 几何平均数在实际应用中有很多限制,如变量值中有一个为零就不能计算几何 平均数,变量值为负值,开偶次根就会形成虚根,失去意义,因此几何平均数比算术 平均数的应用范围窄。 27
27 三、几何平均数 n个变量值乘积的n次方根就是几何平均数。 几何平均数常用于计算合格率、发展速度、利率等变量的平均,因为这类比率的 变量,变量值的连乘积为总比率,不能用算术平均方法,只能用几何平均数计算平均 指标。 几何平均数在实际应用中有很多限制,如变量值中有一个为零就不能计算几何 平均数,变量值为负值,开偶次根就会形成虚根,失去意义,因此几何平均数比算术 平均数的应用范围窄
例1某型号钻头的生产,需要经过6道不同的加工工序,各道工序的 合格率如表所示,试计算平均合格率。 工序名称 冲料 料废 车工 加热 扫槽 接柄 合格率% 98.2 97.5 97.0 96.6 95.5 95.0 x=98.2%x97.5%x.x95%=96.63% 28
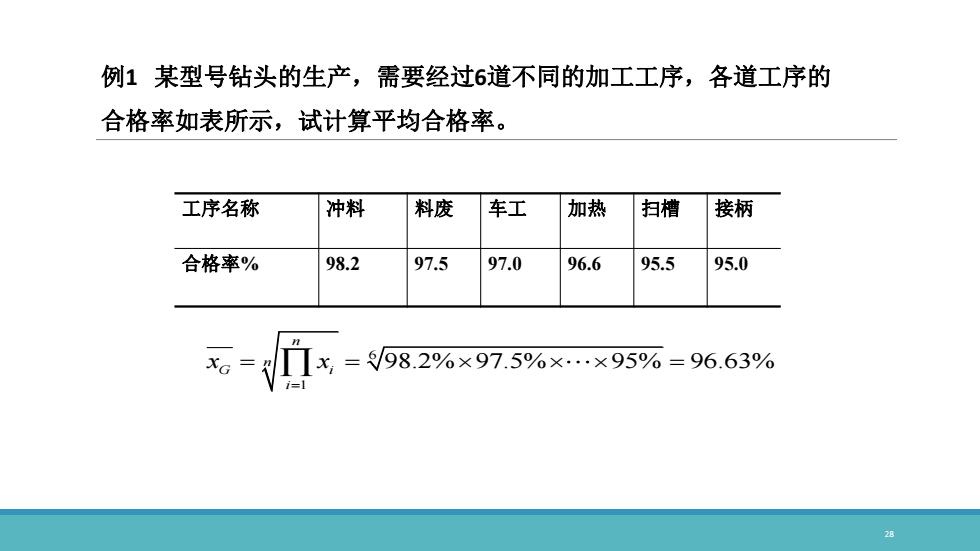
28 例1 某型号钻头的生产,需要经过6道不同的加工工序,各道工序的 合格率如表所示,试计算平均合格率。 工序名称 冲料 料废 车工 加热 扫槽 接柄 合格率% 98.2 97.5 97.0 96.6 95.5 95.0 6 1 98.2% 97.5% 95% 96.63% n n G i i x x

如何理解几何平均数? 一位投资者持有某公司股票,最近四年的收益率分别为4.5%、2.1%、 25.5%、1.9%。要求计算该投资者在这4年内的平均收益率。 Xc= x1-1=/104.5%×102.1%×125.5%×101.9%-1=8.0787% i= 假定该投资者第一年年初投资10000元,按几何收益率计算,第四年年末的 本利和为:10000×104.5%×102.1%×125.5%×101.9%=10000× 108.0787%4=13644.57元 29
29 如何理解几何平均数?
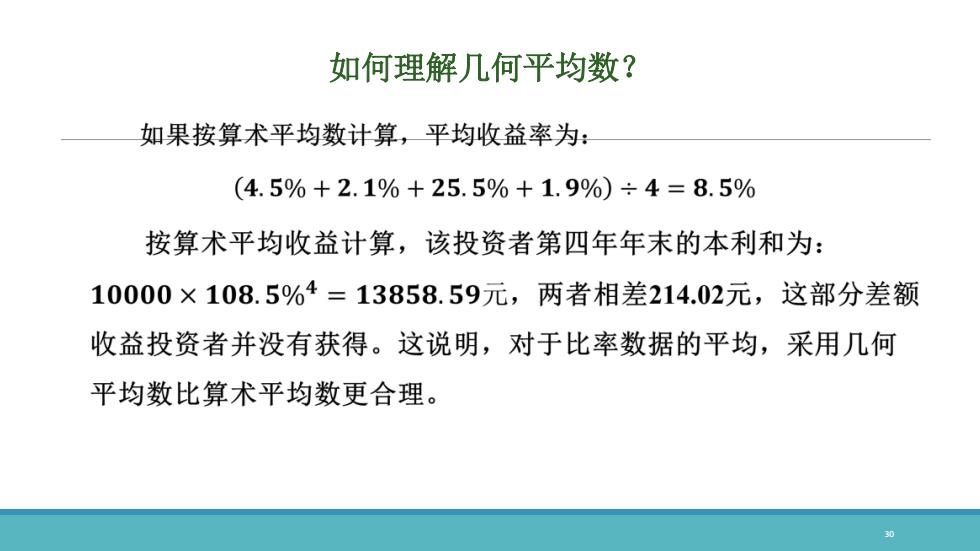
如何理解几何平均数? 如果按算术平均数计算,平均收益率为: (4.5%+2.1%+25.5%+1.9%)÷4=8.5% 按算术平均收益计算,该投资者第四年年末的本利和为: 10000×108.5%4=13858.59元,两者相差214.02元,这部分差额 收益投资者并没有获得。这说明,对于比率数据的平均,采用几何 平均数比算术平均数更合理。 30
30 如何理解几何平均数?