
第5步:优化-寻找最佳的因素水平组合 表1.1.5的设计是73=343个全面试验的部分实施,其中最好的 试验点是值为Y=48.2%的#7。它不一定是全局最好的。人 们想找到满足下式的x*和x3: (x1,x3)=max{(x1,x3)} 这里求取max的区域为: {1≤≤3.4,0.5≤x3≤3.5} 且 (x1,x3)=0.06232+0.25x3-0.06x3+0.0235x1x3
第5步: 优化 - 寻找最佳的因素水平组合 表1.1.5的设计是7 3=343个全面试验的部分实施, 其中最好的 试验点是值为Y= 48.2%的 #7。它不一定是全局最好的。人 们想找到满足下式的x1 *和 x3 * : ˆ ( , ) max ˆ ( 1 , 3 ) * 3 * 1 Y x x = Y x x 这里求取max的区域为: 1 x1 3.4, 0.5 x3 3.5 1 3 2 且 Y ˆ (x1 , x3 ) = 0.06232 + 0.25x3 −0.06x3 + 0.0235x x
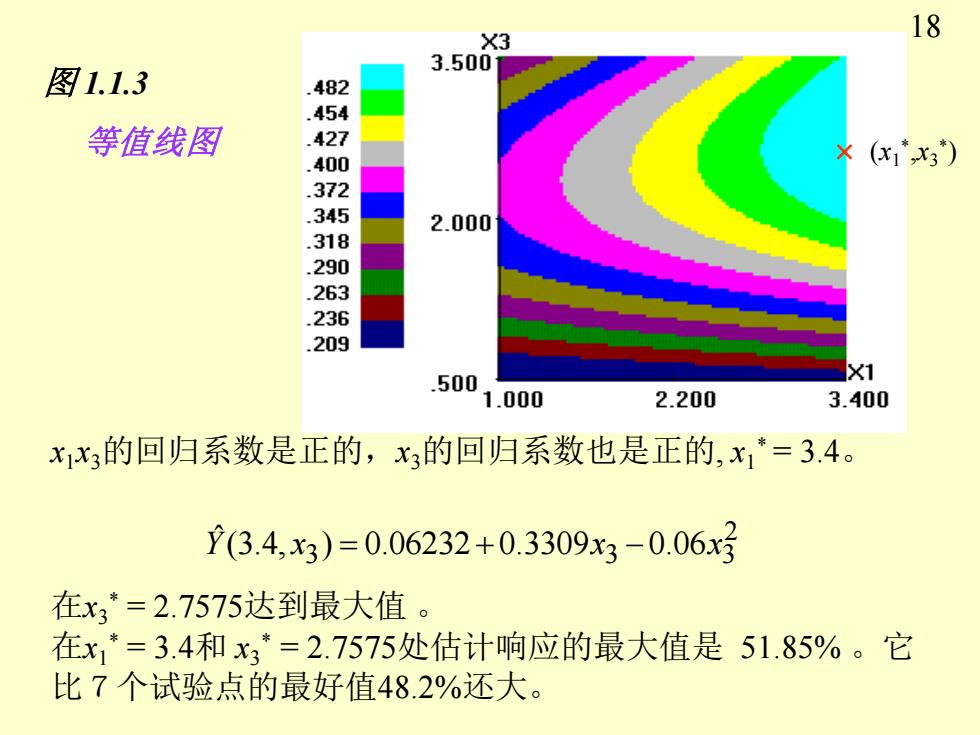
18 ×3 3.500 图1.1.3 .482 .454 等值线图 427 .400 x (1x3) .372 .345 2.000 .318 .290 263 236 209 500 ×1 1.000 2.200 3.400 xx3的回归系数是正的,x3的回归系数也是正的,x=3.4。 Y(3.4,x3)=0.06232+0.3309x3-0.06x3 在x3*=2.7575达到最大值。 在x1*=3.4和x3*=2.7575处估计响应的最大值是51.85%。它 比7个试验点的最好值48.2%还大
x1x3的回归系数是正的,x3的回归系数也是正的, x1 * = 3.4。 2 3 3 06 3 (3.4, ) 0.06232 0.3309 0. Y ˆ x = + x − x 在x3 * = 2.7575达到最大值 。 图 1.1.3 等值线图 (x1 * ,x3 * ) 在x1 * = 3.4和 x3 * = 2.7575处估计响应的最大值是 51.85% 。它 比7个试验点的最好值48.2%还大。 18

讨论: 因素2没有给响应Y予显著的贡献,我们可以选x2为 其中点x2=19ml. 求出的x1*=3.4在边界上,我们需要扩大x的试验上限。 在x1=3.4和x3=2.7575的邻域,追加一些试验是必要的。 在第5步,一些优化算法是很有用的
讨论: 因素 x2 没有给响应Y予显著的贡献,我们可以选x2为 其中点 x2 = 19 ml. 求出的x1 * = 3.4 在边界上, 我们需要扩大x1的试验上限。 在x1 = 3.4和 x3 = 2.7575的邻域,追加一些试验是必要的。 在第5步,一些优化算法是很有用的

混合型水平的均匀设计 试验中各因素若有不同水平数,比如,其 水平数分别为q1,.,qk。 这时应使用相应的混合均匀设计表。见 “方开泰,均匀设计与均匀设计表,科学出版 (1994).” 之附表2
混合型水平的均匀设计 试验中各因素若有不同水平数,比如,其 水平数分别为q1,.,qk。 这时应使用相应的混合均匀设计表。见 “方开泰,均匀设计与均匀设计表,科学出版 (1994).” 之附表2
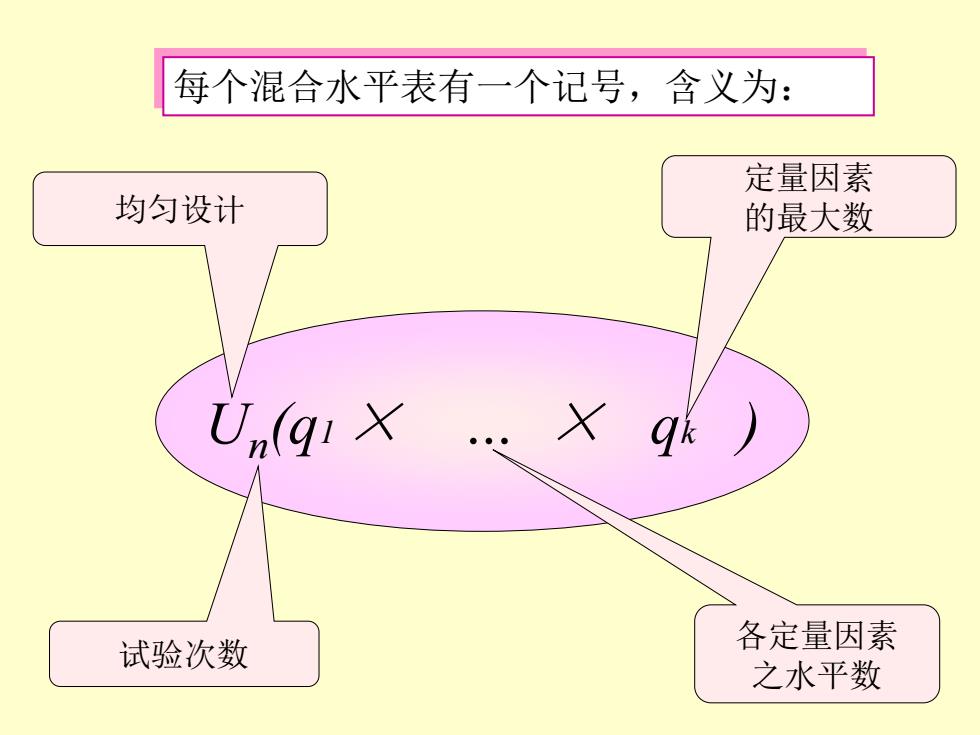
每个混合水平表有一个记号,含义为: 定量因素 均匀设计 的最大数 Un(gix .x ge 试验次数 各定量因素 之水平数
每个混合水平表有一个记号,含义为: Un (q1 × . × qk ) 均匀设计 试验次数 各定量因素 之水平数 定量因素 的最大数