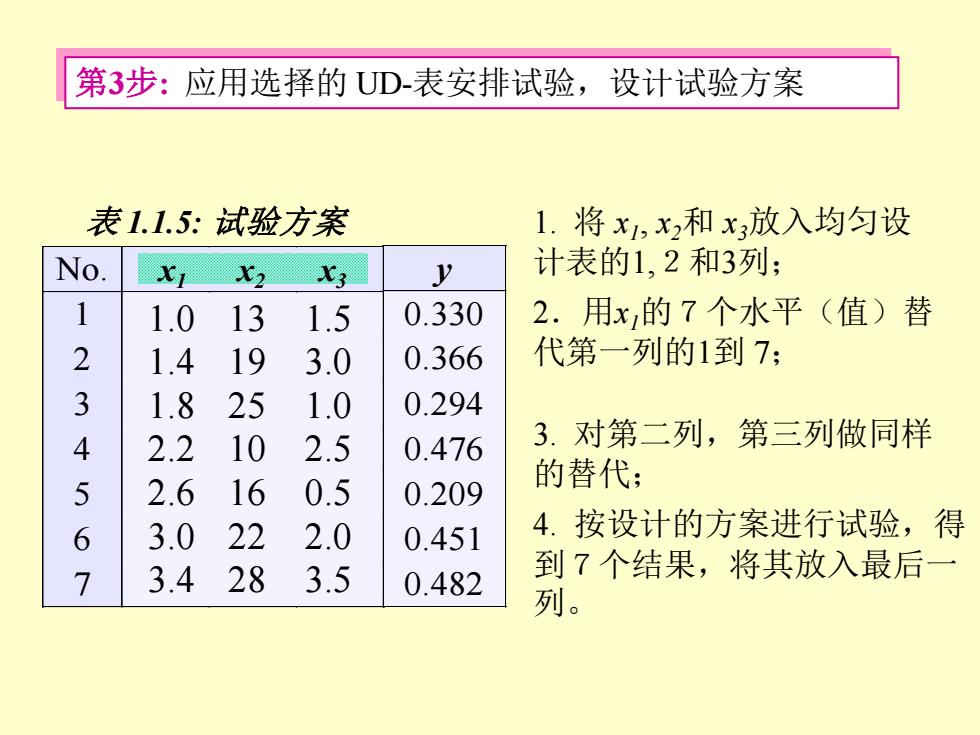
第3步:应用选择的UD-表安排试验,设计试验方案 表1.1.5: 试验方案 1.将x1,x2和x3放入均匀设 No X2 X3 y 计表的1,2和3列; 1 1.0 13 1.5 0.330 2.用x,的7个水平(值)替 2 1.4 19 3.0 0.366 代第一列的1到7: 3 1.8 25 1.0 0.294 4 2.2 10 2.5 0.476 3.对第二列,第三列做同样 5 2.6 16 0.5 0.209 的替代: 6 3.0 22 2.0 0.451 4.按设计的方案进行试验,得 7 34 28 3.5 0.482 到7个结果,将其放入最后一 列
第3步: 应用选择的 UD-表安排试验,设计试验方案 No. 1 2 3 1 1 2 3 2 2 4 6 3 3 6 2 4 4 1 5 5 5 3 1 6 6 5 4 7 7 7 7 1. 将 x1 , x2和 x3放入均匀设 x1 x2 x3 计表的1,2和3列; 2.用x1的7个水平(值)替 代第一列的1到 7; 1.0 1.4 1.8 2.2 2.6 3.0 3.4 3. 对第二列,第三列做同样 的替代; 13 1.5 19 3.0 25 1.0 10 2.5 16 0.5 22 2.0 28 3.5 4. 按设计的方案进行试验,得 到7个结果,将其放入最后一 列。 y 0.330 0.366 0.294 0.476 0.209 0.451 0.482 表 1.1.5: 试验方案

第4步:用回归模型匹配数据 首先,考虑线性回归模型: y=Bo+Bx+B2x2+B3x3+ (1.1.1) 使用回归分析中变量筛选的方法,比如‘向后法’,得到 推荐的模型为: =0.2142+0.0792x3 (1.1.2) 这个结果与人们的经验不符
第 4步: 用回归模型匹配数据 首先,考虑线性回归模型: 这个结果与人们的经验不符。 (1.1.1) 0 1 1 2 2 3 3 y = + x + x + x + 使用回归分析中变量筛选的方法,比如‘向后法’,得到 推荐的模型为: ˆ 0.2142 0.0792 (1.1.2) 3 y = + x

然后,我们尝试用二次回归模型来匹配这些数据: y=Bo+Bx+B2x2+B:x3+Bx+B22x2+B33x3 +B2xx2+B13x1x3+B23x2x3+8 (1.1.3) 使用‘向前’的变量选择法,我们发现适宜的模型: =0.06232+0.25x3-0.06x3+0.0235x1x3 (1.1.4) 表1.1.6:方差分析(ANOVA)表 来源 df SS MS F p 回归 3 0.0621900.020730 43.88 0.006 误差 3 0.0141700.000472 总和 6 0.063608 14
然后,我们尝试用二次回归模型来匹配这些数据: 使用‘向前’的变量选择法,我们发现适宜的模型: (1.1.3) 1 2 1 2 1 3 1 3 2 3 2 3 2 3 3 3 2 2 2 2 2 0 1 1 2 2 3 3 1 1 1 + + + + = + + + + + + x x x x x x y x x x x x x ˆ 0.06232 0.25 0.06 0.0235 (1.1.4) 1 3 2 3 3 y = + x − x + x x 14 来源 df SS MS F p 回归 3 0.062190 0.020730 43.88 0.006 误差 3 0.014170 0.000472 总和 6 0.063608 表 1.1.6: 方差分析(ANOVA)表
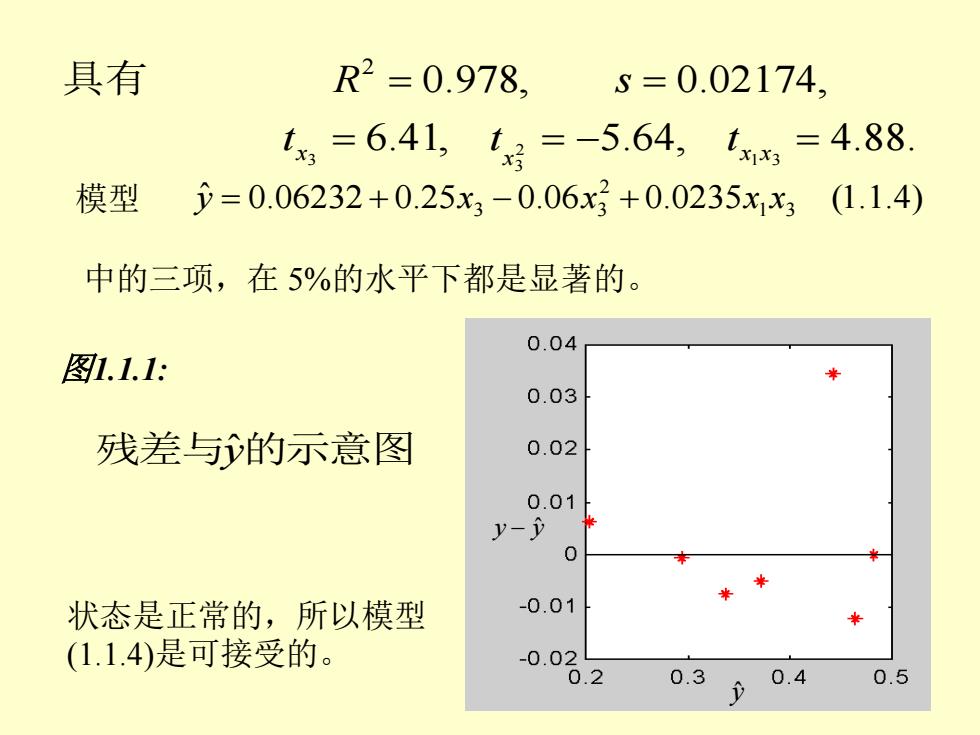
具有 R2=0.978, 5=0.02174, t3=6.41,1x=-5.64,tx=4.88. 模型 y=0.06232+0.25x3-0.06x+0.0235xx3(1.1.4) 中的三项,在5%的水平下都是显著的。 0.04 图1.1.1: 0.03 残差与的示意图 0.02 0.01 y-) 状态是正常的,所以模型 -0.01 (1.1.4)是可接受的。 -0.02 .2 0.3 0.4 0.5
残差与y ˆ的示意图 状态是正常的,所以模型 (1.1.4)是可接受的。 图1.1.1: y ˆ y − y ˆ 6.41, 5.64, 4.88. 0.978, 0.02174, 1 3 2 3 3 2 = = − = = = x x x x t t t 具有 R s 模型 ˆ 0.06232 0.25 0.06 0.0235 (1.1.4) 1 3 2 3 3 y = + x − x + x x 中的三项,在 5%的水平下都是显著的
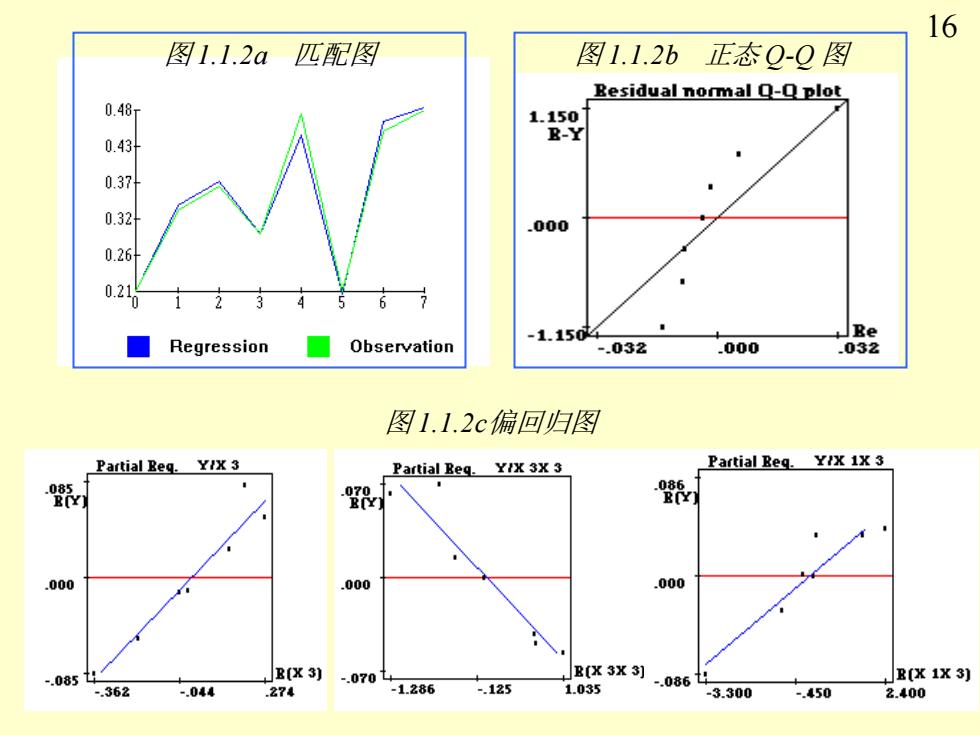
16 图1.1.2a 匹配图 图1.1.2b正态Q-Q图 Besidual nommal Q-Q plot 1.150 B-Y 0.43 0.37 033 000 0.26 0.21 Observation -1.1504 Be Regression -.032 .000 .032 图1.1.2c偏回归图 Partial Req.YIX 3 Partial Beg.YIX 3X 3 Partial Reg.YIX 1X 3 .000 .000 .000 .085t4 B(X 3) -.0704 B(X 3X 3] B(X 1X 3) 362 -.044 .274 1.286 -.125 1.035 -.086 -3.300 -.450 2.400
图 1.1.2a 匹配图 图 1.1.2b 正态 Q-Q 图 图 1.1.2c偏回归图 16