
第一节协方差分析的意义 五、协方差组分的估计 ∑(x-x)y-y) V∑(x-x)2(y-y)2 分子、分母同时除以自由度(n-1),得 ∑(x-x)(y-y)(n-1) V∑(x-x)2/(n-1)V∑y-y)2/(n-1)
五、协方差组分的估计 第一节 协方差分析的意义 − − − − = 2 2 ( ) ( ) ( )( ) x x y y x x y y r 分子、分母同时除以自由度(n-1),得 ( ) /( 1) ( ) /( 1) ( )( )/( 1) 2 2 − − − − − − − = x x n y y n x x y y n r

第一节协方差分析的意义 ∑(x-xy-y)/(n-1) V∑(x-x)2/(n-1)V∑(y-y)2/(n-1) 其中, ∑(x-x)2 是×的均方MSx,是×的总体方差 的无偏估计量。 n-1 ∑y-y)2 2 是y的均方MSy,是y的总体方差 的无偏估计量。 n-1 ∑(x-xy-y) 是×与y的离均差的乘积和,简称均积,记为 n-1 大与均积相对应的总体参数叫协方差,记为COV(x,y) 大均积是协方差的无偏估计量,即EMP,=COV(x,y)
第一节 协方差分析的意义 其中, ( ) /( 1) ( ) /( 1) ( )( )/( 1) 2 2 − − − − − − − = x x n y y n x x y y n r 1 ( ) 2 − − n x x 1 ( ) 2 − − n y y 1 ( )( ) − − − n x x y y 是x的均方MSx,是x的总体方差 的无偏估计量。 2 x 2 是y的均方MS y y,是y的总体方差 的无偏估计量。 是x与y的离均差的乘积和,简称均积,记为 ★与均积相对应的总体参数叫协方差,记为 COV(x, y) MPxy ★均积是协方差的无偏估计量,即 EMP COV(x, y) xy =

第一节协方差分析的意义 ∑(x-x(y-y)/(n-1) 正法显示该图 ∑(x-x2n-1V∑少-丹2(-1) 于是,相关系数可以表示为: MP MS,MS, 相应的总体相关系数可以表示为: COV(x,y) 00y OxOy
第一节 协方差分析的意义 于是,相关系数可以表示为: ( ) /( 1) ( ) /( 1) ( )( )/( 1) 2 2 − − − − − − − = x x n y y n x x y y n r x y xy MS MS MP r = 相应的总体相关系数可以表示为: x y xy x y COV x y = = ( , )

第一节协方差分析的意义 大均积与均方具有相似的形式,也有相似的性质 无法显示该图片 大方差分析时,一个变量的总平方和与自由度可按变 异来源进行剖分,进而求得相应的均方。 大同样,两个变量的总乘积和自由度也可按变异来源 进行剖分,从而获得相应的均积。 把两个变量的总乘积和与自由度按变异来 源进行剖分,并获得相应的均积的方法,也称为 协方差分析
第一节 协方差分析的意义 ★均积与均方具有相似的形式,也有相似的性质。 ★方差分析时,一个变量的总平方和与自由度可按变 异来源进行剖分,进而求得相应的均方。 ★同样,两个变量的总乘积和自由度也可按变异来源 进行剖分,从而获得相应的均积。 把两个变量的总乘积和与自由度按变异来 源进行剖分,并获得相应的均积的方法,也称为 协方差分析
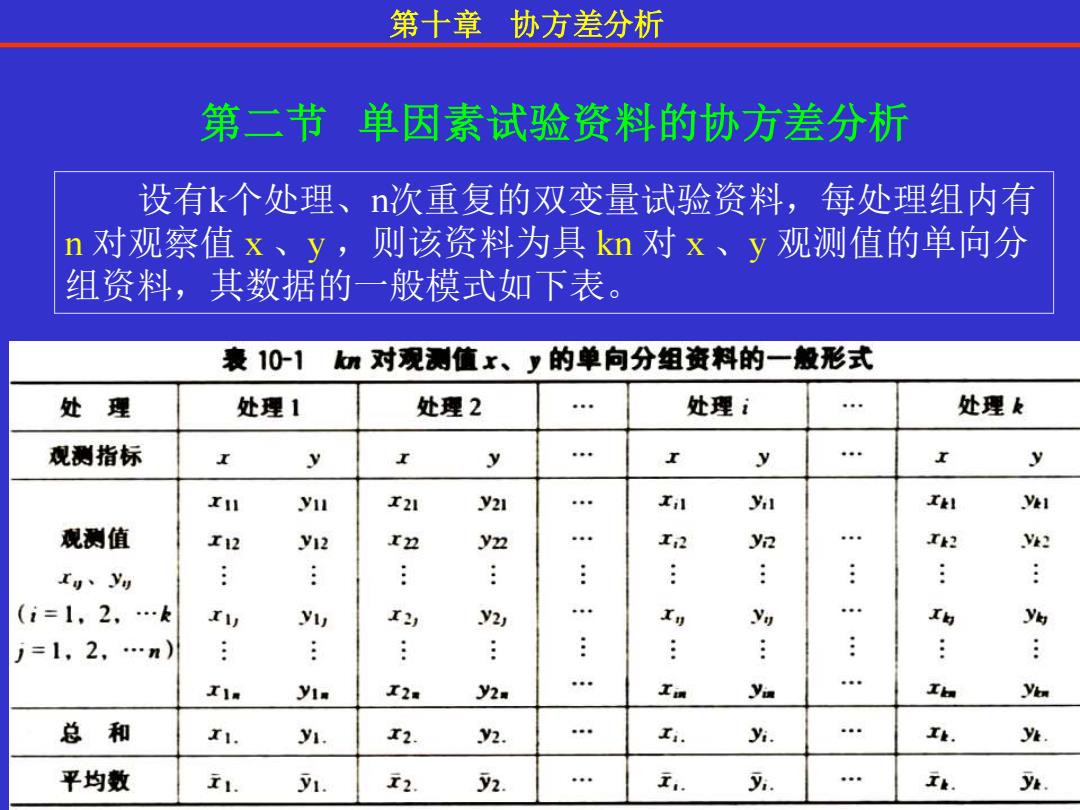
第十章协方差分析 第三节单因素试验资料的协方差分析 设有k个处理、次重复的双变量试验资料,每处理组内有 n对观察值x、y,则该资料为具kn对x、y观测值的单向分 组资料,其数据的一般模式如下表。 表101对观测值x、y的单向分组资料的一般形式 处理 处理1 处理2 .. 处理i 处理k 观测指标 y 。年 y . y xn y11 I21 y21 Jil y ZH y:1 观测值 x12 y12 In yn In y2 TH2 : rg、yg (i=1,2、…k I\ y 12 y2, Iy g Ik yh j=1,2,…n) x1. y1. I2s y2m 工m yin Ih yin 总和 r1. y1. x2. 2. Ii. yi. Ik. % 平均数 i1. y1. r2. y2. 000 工. Bi. 年0 Ih
第二节 单因素试验资料的协方差分析 第十章 协方差分析 设有k个处理、n次重复的双变量试验资料,每处理组内有 n 对观察值 x 、y ,则该资料为具 kn 对 x 、y 观测值的单向分 组资料,其数据的一般模式如下表