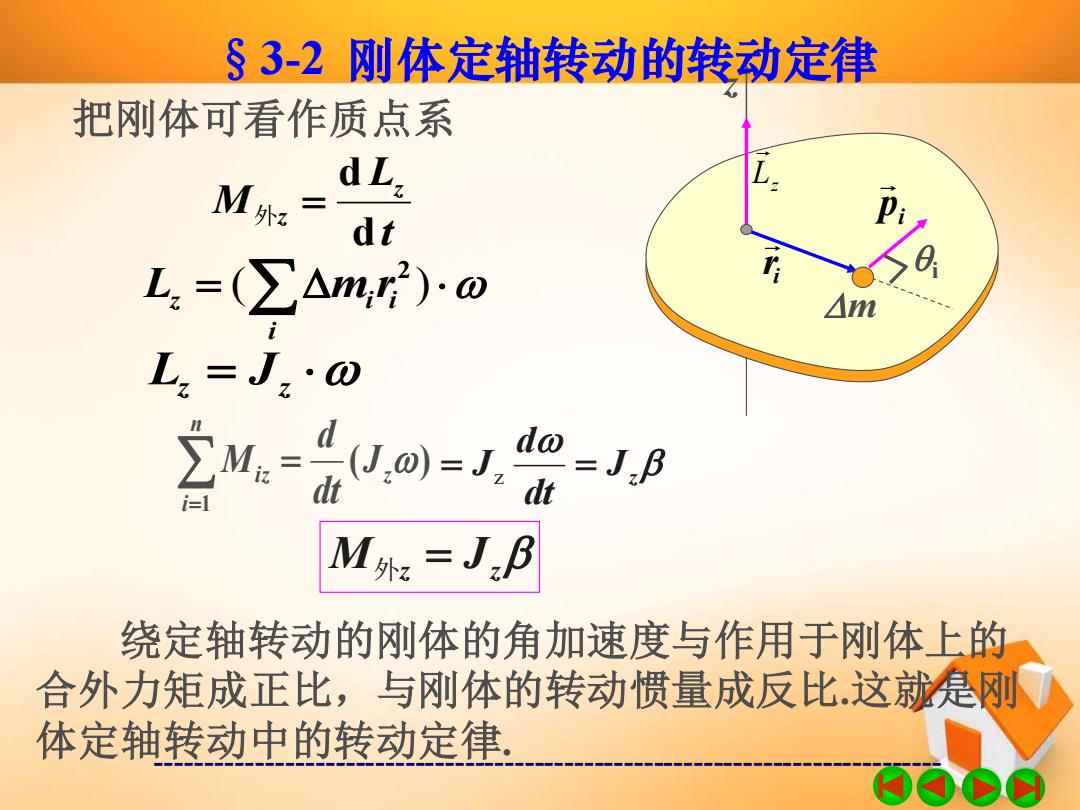
§3-2刚体定轴转动的转动定律 把刚体可看作质点系 M外z= dL: dt L,=(∑△m,)o △m L2=J2·0 M外:=JB 绕定轴转动的刚体的角加速度与作用于刚体上的 合外力矩成正比,与刚体的转动惯量成反比.这就是刚 体定轴转动中的转动定律
------------------------------------------------------------------------------- 把刚体可看作质点系 Lz z i r m i i p t L M z z d d 外 = = ( ) i z i i L m r 2 Lz = Jz ( ) 1 z n i iz J dt d M = = Jz dt d = Jz = M外z = Jz 绕定轴转动的刚体的角加速度与作用于刚体上的 合外力矩成正比,与刚体的转动惯量成反比.这就是刚 体定轴转动中的转动定律. §3-2 刚体定轴转动的转动定律
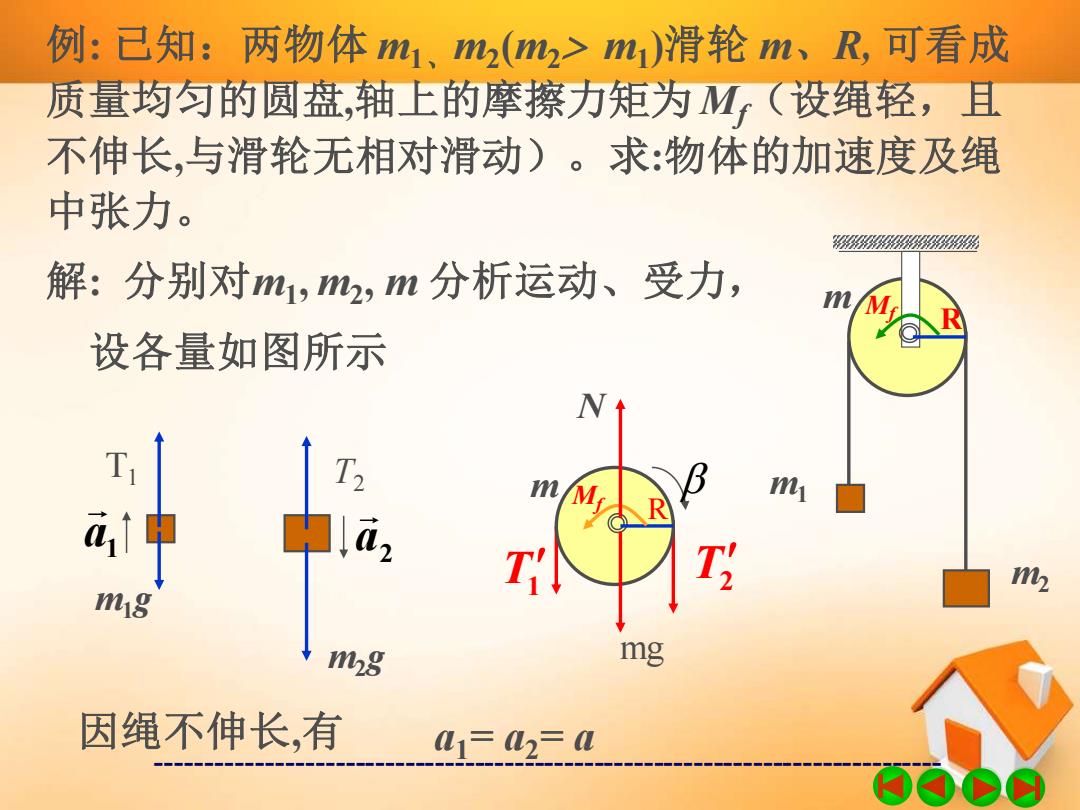
例:已知:两物体m1、m2(m2>m1)滑轮m、R,可看成 质量均匀的圆盘,轴上的摩擦力矩为M(设绳轻,且 不伸长,与滑轮无相对滑动)。求:物体的加速度及绳 中张力。 解:分别对m1,m2,m分析运动、受力, 设各量如图所示 R 白 T T 2 m18 mg mg 因绳不伸长,有 L1=2=M
------------------------------------------------------------------------------- 例: 已知:两物体 m1、 m2 (m2 m1 )滑轮 m、R, 可看成 质量均匀的圆盘,轴上的摩擦力矩为 Mf(设绳轻,且 不伸长,与滑轮无相对滑动)。求:物体的加速度及绳 中张力。 m1 m2 m R Mf 解: 分别对m1 , m2 , m 分析运动、受力, 设各量如图所示 1 a m1g T1 a2 m2g T2 T2 T1 m R Mf mg N 因绳不伸长,有 a1= a2= a