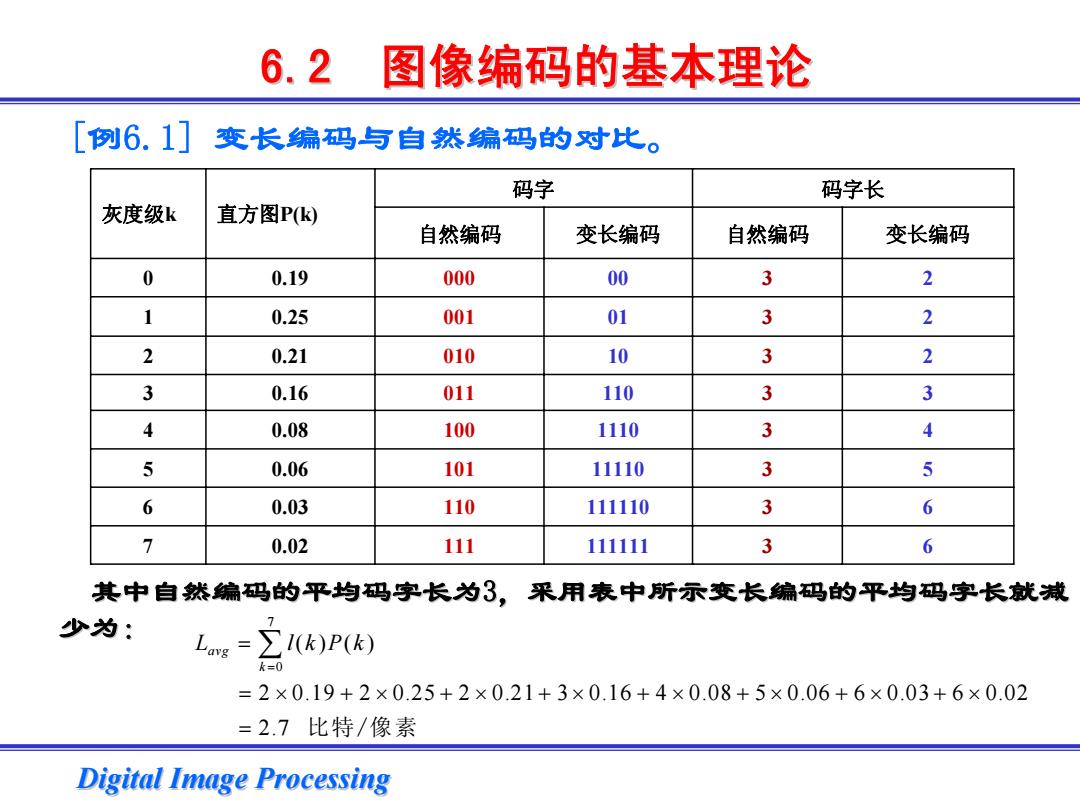
6.2图像编码的基本理论 [例6.1] 变长编码与自然编码的对比。 码字 码字长 灰度级k 直方图Pk 自然编码 变长编码 自然编码 变长编码 0 0.19 000 00 3 2 1 0.25 001 01 3 2 2 0.21 010 10 3 2 3 0.16 011 110 3 3 4 0.08 100 1110 3 4 5 0.06 101 11110 3 5 6 0.03 110 111110 3 6 7 0.02 111 111111 3 6 其中自然编码的平均码字长为3,采用表中所示变长编码的平均码字长就减 少为: z1()P() k=0 =2×0.19+2×0.25+2×0.21+3×0.16+4×0.08+5×0.06+6×0.03+6×0.02 =2.7比特/像素 Digital Image Processing
Digital Image Processing Digital Image Processing [例6.1] 变长编码与自然编码的对比。 6.2 图像编码的基本理论 图像编码的基本理论 码字 码字长 自然编码 变长编码 自然编码 变长编码 0 0.19 000 00 3 2 1 0.25 001 01 3 2 2 0.21 010 10 3 2 3 0.16 011 110 3 3 4 0.08 100 1110 3 4 5 0.06 101 11110 3 5 6 0.03 110 111110 3 6 7 0.02 111 111111 3 6 灰度级k 直方图P(k) 其中自然编码的平均码字长为3,采用表中所示变长编码的平均码字长就减 少为: 7 0 () () 2 0.19 2 0.25 2 0.21 3 0.16 4 0.08 5 0.06 6 0.03 6 0.02 2.7 avg k L lkPk = = = × +× +× +× +× +× +× +× = ∑ 比特/像素
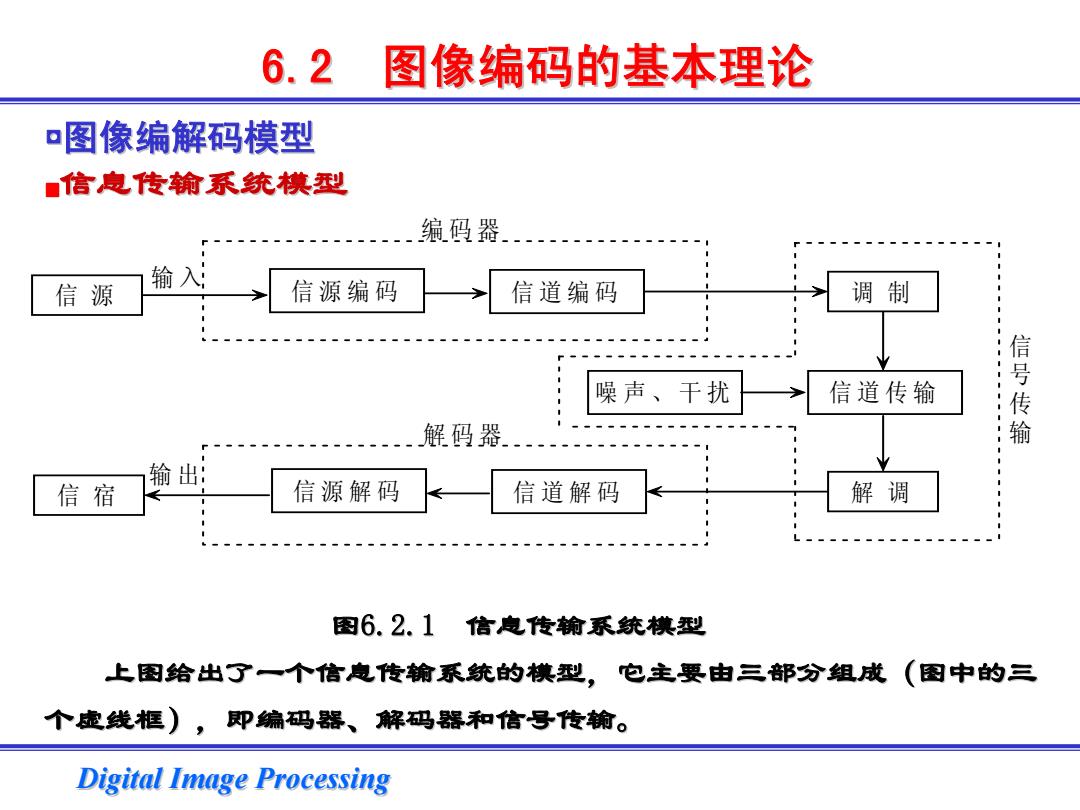
6.2 图像编码的基本理论 ¤图像编解码模型 信息传输系统模型 编码器 信源 输入; 信源编码 信道编码 调制 信 噪声、干扰 信道传输 传 解码器」 输出 信宿 信源解码 信道解码 解调 图6.2.1 信息传输系统模型 上图给出了一个信息传输系统的模型,它主要由三部分组成(图中的三 个虚线框),即编码器、 解码器和信号传输。 Digital Image Processing
Digital Image Processing Digital Image Processing ◘图像编解码模型 图像编解码模型 ▓信息传输系统模型 信息传输系统模型 图6.2.1 信息传输系统模型 上图给出了一个信息传输系统的模型,它主要由三部分组成(图中的三 个虚线框),即编码器、解码器和信号传输。 6.2 图像编码的基本理论 图像编码的基本理论 信 源 信源编码 信道编码 调 制 信道传输 解 调 噪声、干扰 信 宿 信源解码 信道解码 输 入 输 出 编码器 解码器 信 号 传 输
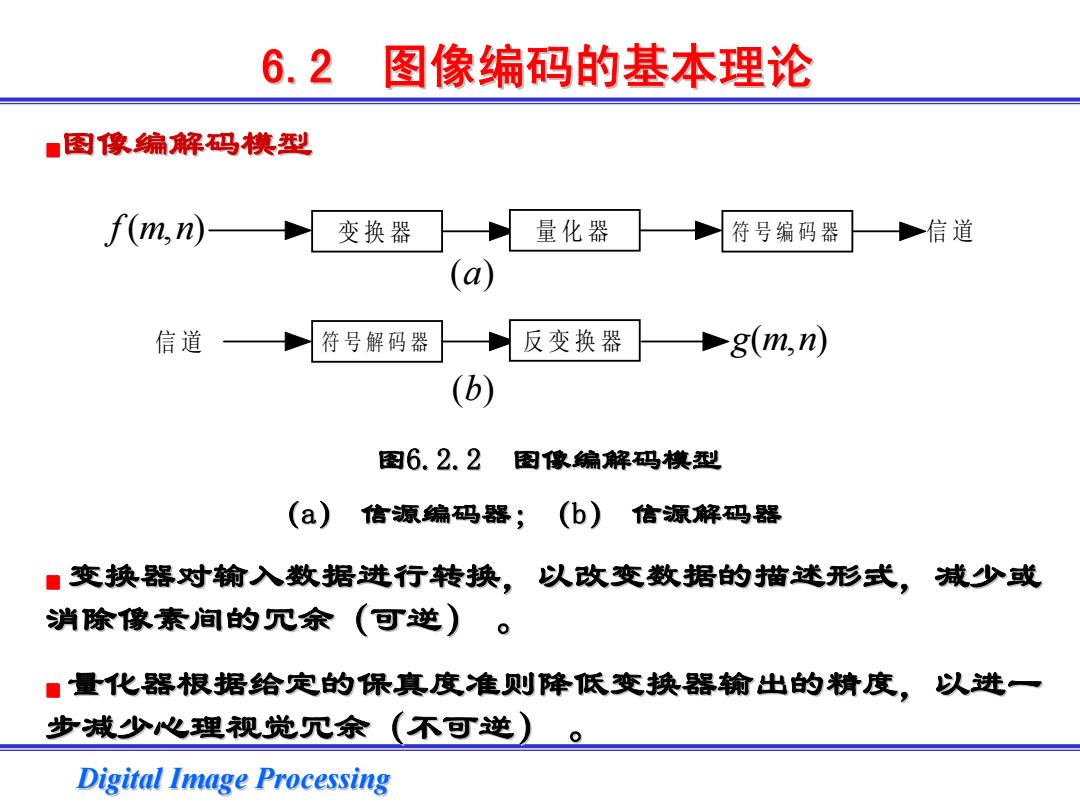
6.2 图像编码的基本理论 图像编解码模型 f(m,n)- 变换器 量化器 符号编码器 ◆信道 (a) 信道 符号解码器 反变换器 +8m,n) (b) 图6.2.2 图像编解码模型 (a) 信源编码器, (b) 信源解码器 ■变换器对输入数据进行转换,以改变数据的描述形式。 减少或 消除像素间的冗余(可逆) ■量化器根据给定的保真度准则降低变换器输出的精度,以进一 步减少心理视觉冗余(不可逆) Digital Image Processing
Digital Image Processing Digital Image Processing 6.2 图像编码的基本理论 图像编码的基本理论 ▓图像编解码模型 图像编解码模型 图6.2.2 图像编解码模型 (a) 信源编码器;(b) 信源解码器 ▓ 变换器对输入数据进行转换,以改变数据的描述形式,减少或 变换器对输入数据进行转换,以改变数据的描述形式,减少或 消除像素间的冗余(可逆) 消除像素间的冗余(可逆) 。 ▓ 量化器根据给定的保真度准则降低变换器输出的精度,以进一 量化器根据给定的保真度准则降低变换器输出的精度,以进一 步减少心理视觉冗余(不可逆) 步减少心理视觉冗余(不可逆) 。 nmf ),( 变换器 量化器 符号编码器 信 道 信 道 符号解码器 反变换器 nmg ),( a)( b)(

6.2 图像编码的基本理论 ¤保真度准则 对图像的失真程度或质量进行评价,以便将图像失真限 制在给定的范围内。 客观保真度准则 将信息损失的多少,表示为原给图像与压缩后又解压缩 得到的重建图像的函数,就称为客观保真度准则。通常以均 方根误差、均方根信噪比和峰值信噪比三种形式来表示。 (1)均方根(RMS)误差 若原图像为fm,n心),压缩又解压后的图像为g(1),则 误差图像为: e(m,n)=g(m,n)-f(m,n) Digital Image Processing
Digital Image Processing Digital Image Processing 6.2 图像编码的基本理论 图像编码的基本理论 ◘保真度准则 对图像的失真程度或质量进行评价,以便将图像失真限 对图像的失真程度或质量进行评价,以便将图像失真限 制在给定的范围内。 制在给定的范围内。 ▓客观保真度准则 客观保真度准则 将信息损失的多少,表示为原始图像与压缩后又解压缩 将信息损失的多少,表示为原始图像与压缩后又解压缩 得到的重建图像的函数,就称为客观保真度准则。通常以均 得到的重建图像的函数,就称为客观保真度准则。通常以均 方根误差、均方根信噪比和峰值信噪比三种形式来表示。 方根误差、均方根信噪比和峰值信噪比三种形式来表示。 (1)均方根(RMS)误差 若原图像为f(m,n),压缩又解压后的图像为 ,压缩又解压后的图像为g(m,n),则 误差图像为: em n gm n f m n ( ,) ( ,) ( ,) = −

6.2 图像编码的基本理论 均方根 (RMS) 误差为: [2a网j-{22amjr M-1N-1 M-N 1=0 (2)均方根信噪比SNR, 令g(m,n)=f(m,n)+n(m,n)=f(m,n)+e(n,m),即把重建图 像g,n和输入图像fm,)之间的误差看作是噪声,将重建图 像信噪比SNR作为保真度准则,即 (m.) M-1N-1 ∑∑f(m,n) SNRS= m=0n=0 =01=0 M-1N-1 M-1N-1 ∑e(m ∑∑[g(m,)-f(mn] =0=0 Digital Image Processing
Digital Image Processing Digital Image Processing 6.2 图像编码的基本理论 图像编码的基本理论 均方根(RMS)误差为: (2)均方根信噪比 )均方根信噪比 令 ,即把重建图 像g(m,n)和输入图像f(m,n)之间的误差看作是噪声,将重建图 之间的误差看作是噪声,将重建图 像信噪比SNR作为保真度准则,即 作为保真度准则,即 ( ) ( )( ) 1 1 1 1 1 1 2 2 2 1 1 2 0 0 0 0 , , , M N M N rms MN MN m n m n e e mn g mn f mn − − − − = = = = ⎡ ⎤ ⎧ ⎫ = =− ⎢ ⎥ ⎨ ⎡⎣ ⎤⎦ ⎬ ⎣ ⎦ ⎩ ⎭ ∑ ∑ ∑ ∑ SNRrms ( ) ( ) ( ) ( )( ) 1 1 1 1 1 1 2 2 2 2 0 0 0 0 1 1 1 1 2 2 0 0 0 0 , , , ,, M N M N m n m n rms M N M N m n m n f mn f mn SNR e mn g mn f mn − − − − = = = = − − − − = = = = ⎡ ⎤ ⎧ ⎫ ⎢ ⎥ ⎪ ⎪ ⎪ ⎪ = = ⎢ ⎥ ⎨ ⎬ ⎢ ⎥ ⎪ ⎡ ⎤ − ⎪ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ ⎩⎪ ⎭⎪ ∑ ∑ ∑ ∑ ∑∑ ∑∑ g( ,) ( ,) ( ,) ( ,) ( ,) m n = += + f mn mn η f mn emn