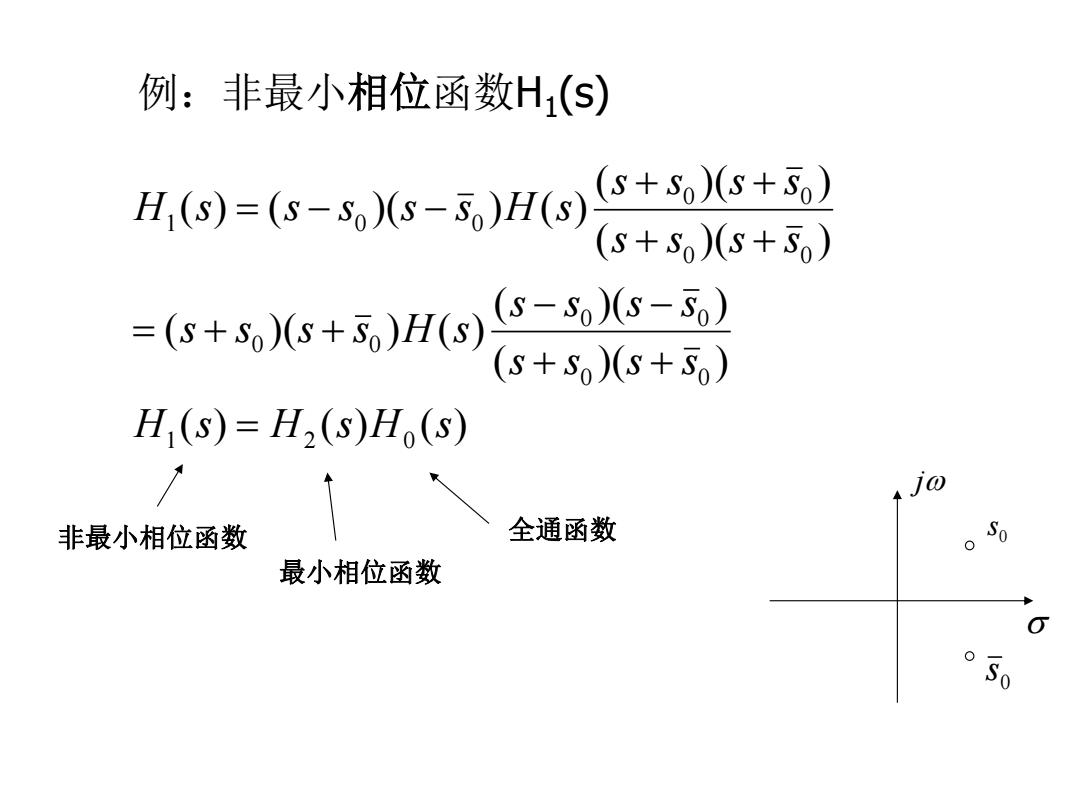
例:非最小相位函数H1(S) H,(S)=(6-ss-)Hs)S+5+ (s+S)(s+5) =(6+o)6+5,)H0s)S-s-5) (s+S)(s+S) H(s)=H2(s)H(s) 非最小相位函数 全通函数 So 最小相位函数 。S0
例:非最小相位函数H1 (s) j 0 s 0 s ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 2 0 0 0 0 0 0 0 0 0 0 0 1 0 0 H s H s H s s s s s s s s s s s s s H s s s s s s s s s H s s s s s H s 最小相位函数 非最小相位函数 全通函数

7-2、希尔伯特变换 F(S)= N(s)ans"+amsm+.+as+do D(s) bns”+bn-1s”-+.+bs+bo E,(S)+O,(S) E,(S)+0,S) 偶函数 奇函数 可以进一步: F)= N(s)D(-S)_[E(s)+O(s)][E2(-S)+O2(-S)] D(S)D(-S)[E2(s)+O2(S)][E2(-S)+O2(-S)] -[E(⊙+O(s][E,(s)-0,(s】_E,E2-0,02+0,E2-0,E [E2(s)+O2(s][E2(s)-O2(s)] E(s)-O2(s) EE2-QO:O.E:-O.E=EvF(s)+OdF(s) E2(s)-2(s)E2(s)-2(s) 偶部 奇部
7-2、希尔伯特变换 ( ) ( ) ( ) ( ) ... ... ( ) ( ) ( ) 2 2 1 1 1 0 1 1 1 0 1 1 E s O s E s O s b s b s b s b a s a s a s a D s N s F s n n n n m m m m 奇函数 可以进一步: 偶函数 ( ) ( ) ( ) ( ) ( ) ( ) [ ( ) ( )][ ( ) ( ) ] ( ) ( ) [ ( ) ( )][ ( ) ( ) ] [ ( ) ( )][ ( ) ( ) ] [ ( ) ( )][ ( ) ( ) ] ( ) ( ) ( ) ( ) ( ) 2 2 2 2 1 2 2 1 2 2 2 2 1 2 1 2 2 2 2 2 1 2 1 2 1 2 2 1 2 2 2 2 1 1 2 2 2 2 2 2 1 1 2 2 EvF s OdF s E s O s O E O E E s O s E E O O E s O s E E O O O E O E E s O s E s O s E s O s E s O s E s O s E s O s E s O s E s O s D s D s D s N s F s 偶部 奇部

EvF(s)=[F(s)+Fs OdF(s)=[F(s)-F(-5) 令:s=j0 F(jo)=EvF(jo)+OdF(jo) EvF(jo)=Re[F(jo)] OdF(jo)=Im[F(jo)] F(jo)=Re F(jo)]+jlm F(jo) ↑ ↑ 实部 虚部 注意:网络函数的实部与虚部非独立
[ ( ) ( )] 2 1 ( ) [ ( ) ( )] 2 1 ( ) OdF s F s F s EvF s F s F s ( ) Re[ ( ) ] Im[ ( ) ] ( ) Im[ ( ) ] ( ) Re[ ( ) ] ( ) ( ) ( ) F j F j j F j OdF j F j EvF j F j F j EvF j OdF j s j 实部 虚部 令: 注意:网络函数的实部与虚部非独立