
什么是判定树? 举例: 12个球如何用天平只称3次便分出轻重? 分析: 12个球中必有一个非轻即重,即共有24种“次品”的可能性。 每次天平称重的结果有3种,连称3次应该得到的结果有33=27 说明仅用3次就能找出次品的可能性是存在的。 思路: 首先,将12个球分三组,每组4个,任意取两组称。会有两种情 况:平衡,或不平衡。 其次,一定要利用已经称过的那些结论;即充分利用“旧球”的 标准性作为参考。 6
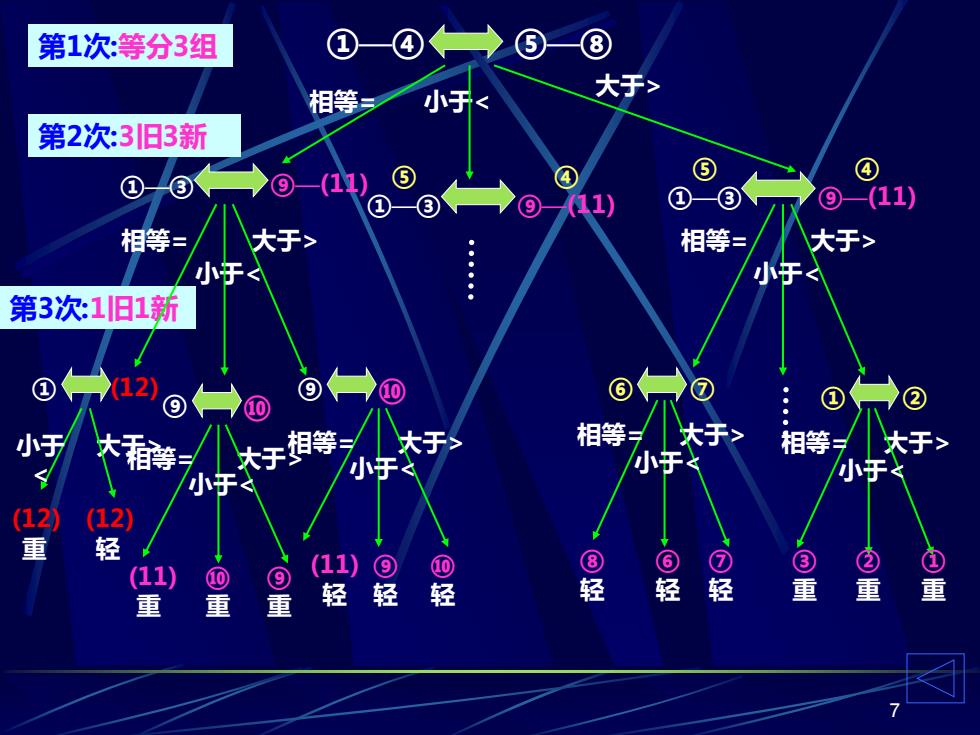
6 什么是判定树? 举例: 12个球如何用天平只称3次便分出轻重? 分析: 12个球中必有一个非轻即重,即共有24种“次品”的可能性。 每次天平称重的结果有3种,连称3次应该得到的结果有3 3=27 种。 说明仅用3次就能找出次品的可能性是存在的。 思路: 首先,将12个球分三组,每组4个,任意取两组称。会有两种情 况:平衡,或不平衡。 其次,一定要利用已经称过的那些结论;即充分利用“旧球”的 标准性作为参考
第1次:等分3组 ④ ⑤⑧ 相等 小于 大于> 第2次:3旧3新 ⑤ ④ ⑤ ④ ①③ ⑨-(11) ①® ⑨ 11 ①® ⑨(11) 相等= 大于> 相等= 大于> 小杆 小< 第3次:1旧1新 ① 12 ⑥ ⑦ ① 小 相等 大于相等 大于 相等 于 相等 小年 (12) (12) 重 轻 (11)⑨ ⑧ (6 ⑦ ② 11) ⑨ 轻 轻 轻 轻 轻 轻 重 重 重 重 重
7 第1次:等分3组 第2次:3旧3新 第3次:1旧1新 ①—④ ⑤—⑧ 相等= 小于< 大于> ①—③ ⑨—(11) 相等= 大于> 小于< ⑤ ①—③ ④ ⑨—(11) ⑤ ①—③ ④ ⑨—(11) 大于> 小于< 相等= 大于> 小于< 相等= ① (12) 小于 < (12) 重 大于> (12) 轻 ⑨ ⑩ 大于> 小于< 相等= (11) 重 ⑩ 重 ⑨ 重 ⑨ ⑩ 大于> 小于< 相等= (11) 轻 ⑩ 轻 ⑨ 轻 ⑥ ⑦ ⑧ 轻 ⑦ 轻 ⑥ 轻 ① ② 大于> 小于< 相等= ③ 重 ① 重 ② 重
什么是带权树? 即路径带有权值。例如: 4 a 8
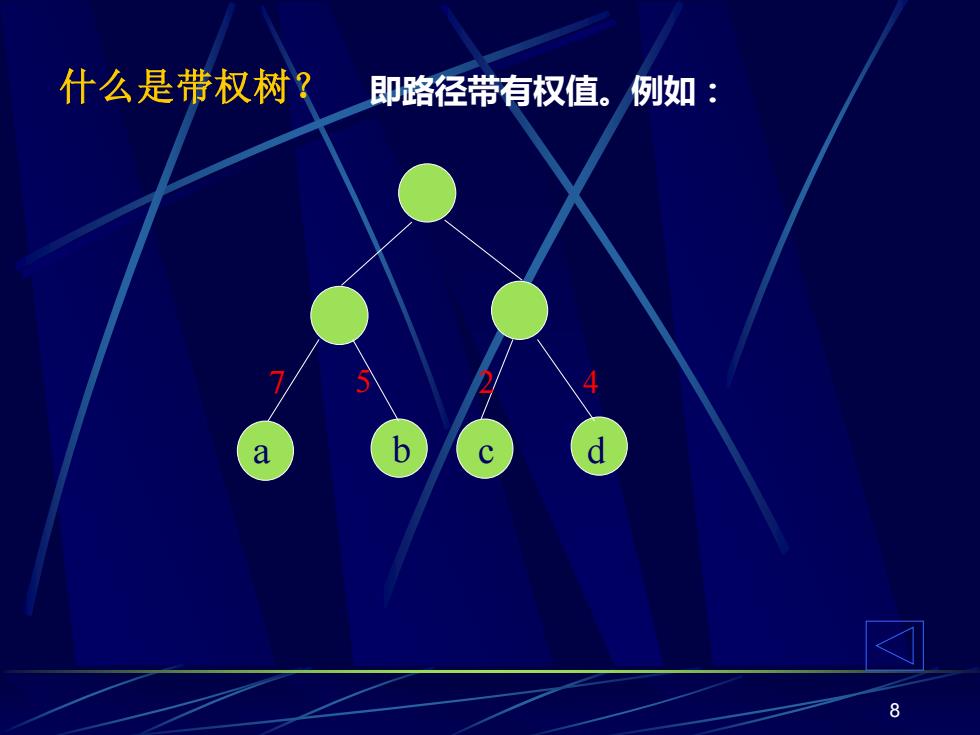
8 什么是带权树? a b c d 7 5 2 4 即路径带有权值。例如:
6.5 Huffman树及其应用 Huffman?树 二、Huffman编码 带权路径 长度最短 的树 Huffman树 最优二叉树 是通信 Huffman编码 不等长编码 中最经 典的压 缩编码 9
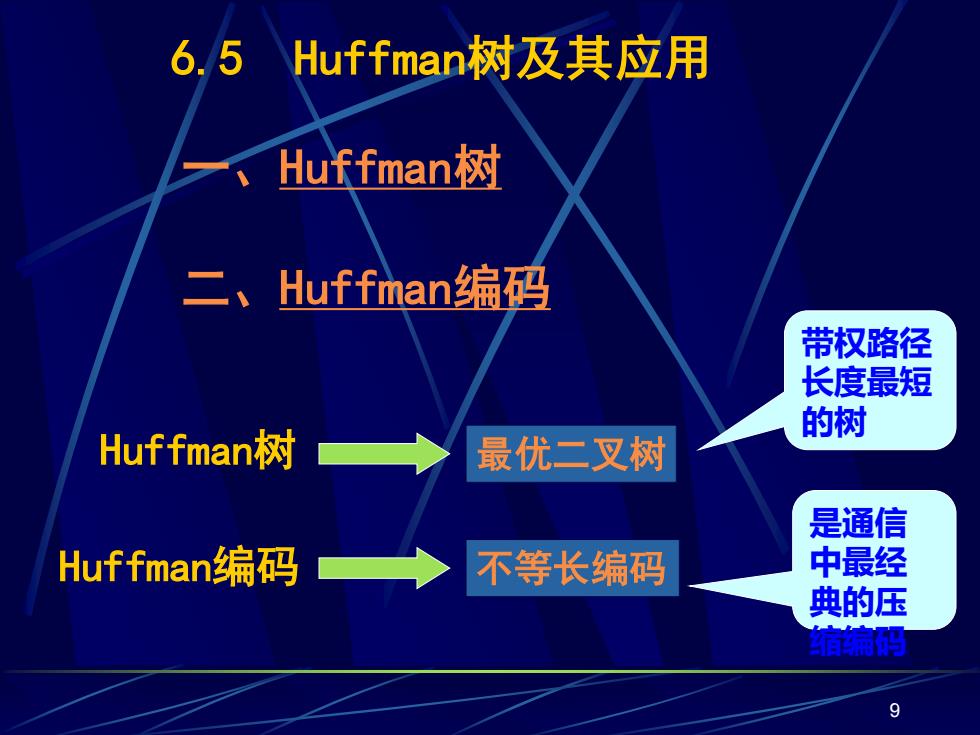
9 6.5 Huffman树及其应用 一、Huffman树 二、Huffman编码 Huffman树 最优二叉树 Huffman编码 带权路径 长度最短 的树 不等长编码 是通信 中最经 典的压 缩编码