北京化工大学：《材料力学》课程教学课件（PPT讲稿）第七章 应力和应变分析、强度理论

§7.3二向应力状态分析一解析法 6 27

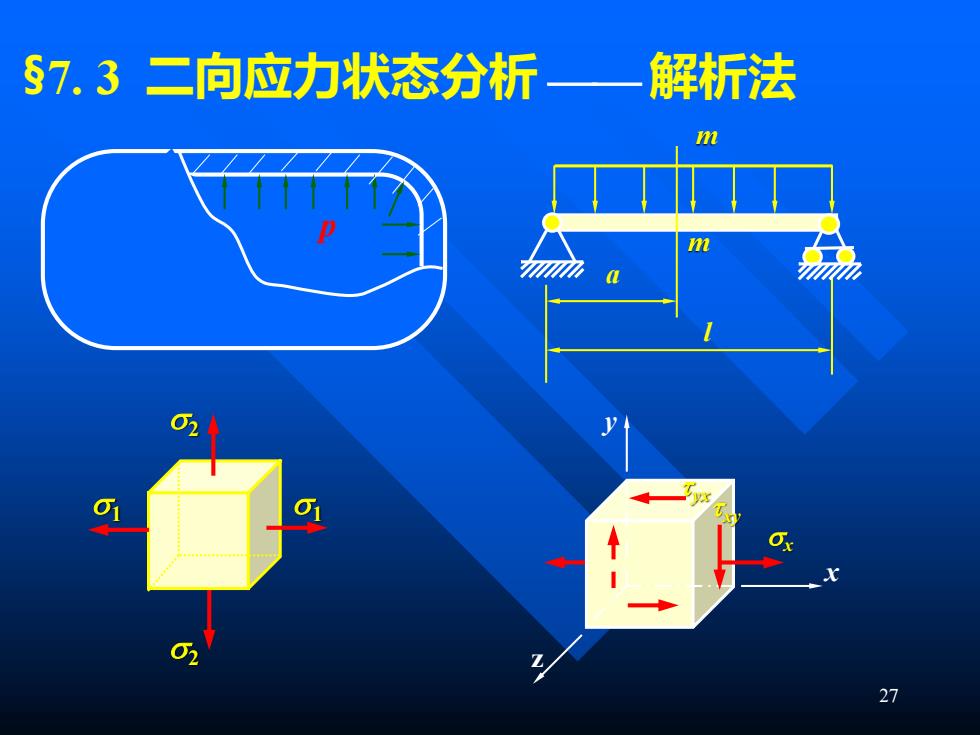
27 §7. 3 二向应力状态分析 ⎯⎯ 解析法 p m m a l 2 2 1 1 x x y z  xy  yx

U K 应力状态分析 在已知过一点的某些截面上 的应力时，求出过该点的任 Ox 一截面上的应力，从而求出 主应力和主平面。 二向应力状态的表示 切应力的下标 作用面的法线 切应力的方向 28

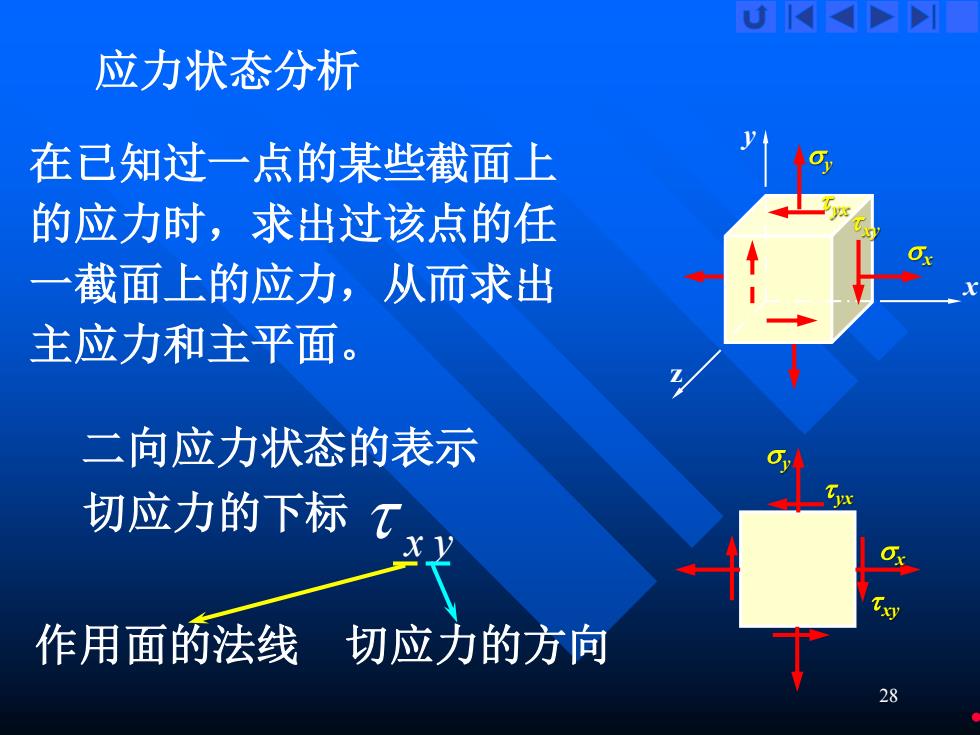
28 二向应力状态的表示 应力状态分析 在已知过一点的某些截面上 的应力时，求出过该点的任 一截面上的应力，从而求出 主应力和主平面。 x y 切应力的下标  作用面的法线 切应力的方向 x x y z y  xy  yx x y  xy  yx

二向应力状态的表示 切应力的下标T 6 作用面的法线 切应力的方向 正负号规定 正应力 拉为正 压为负 29

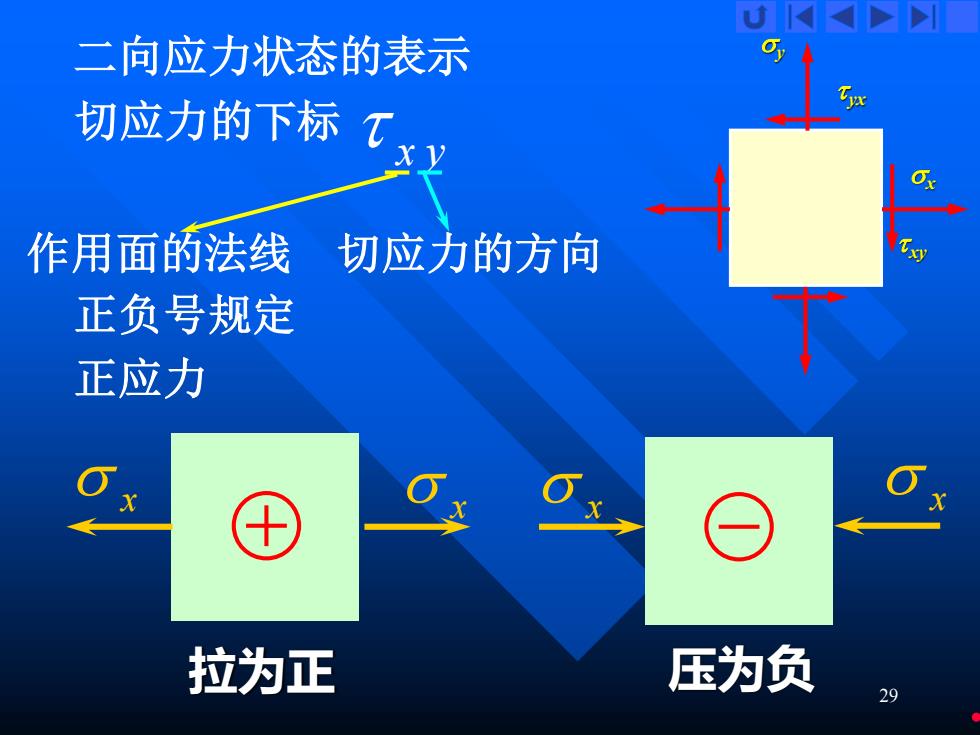
29 二向应力状态的表示 x y 切应力的下标  作用面的法线 切应力的方向 正负号规定 正应力  x  x 拉为正 压为负  x  x x y  xy  yx

U K 切应力 使单元体顺时针方向转动 为正；反之为负。 截面的方向角 n 由x正向逆时针转到截面的 X ⊕ 外法线n的正向的c角为正； 反之为负。 30

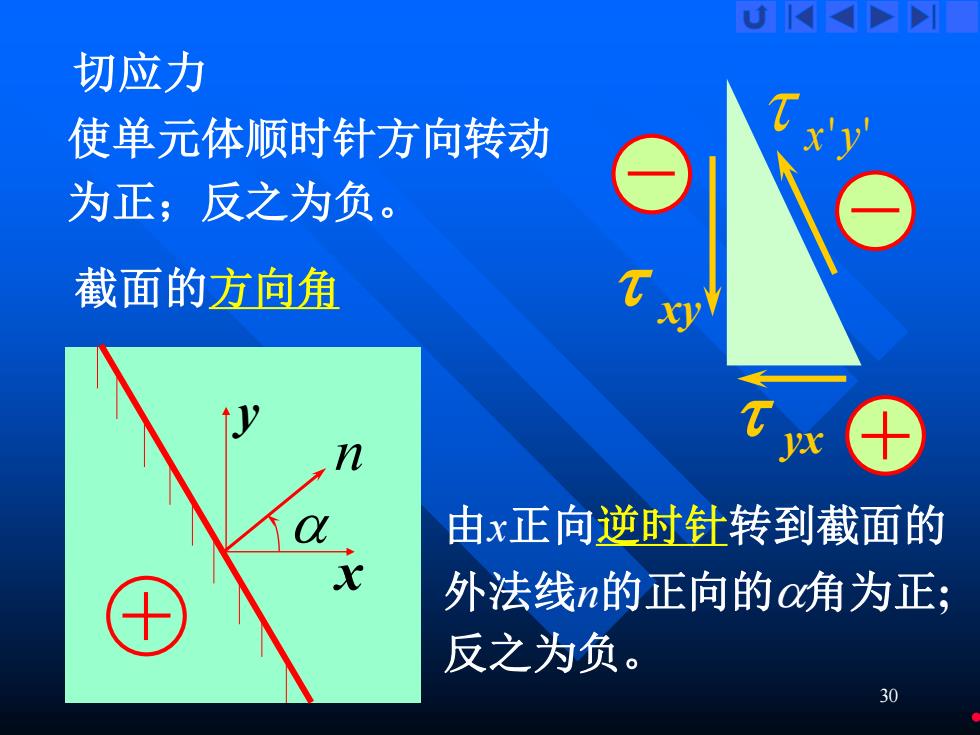
30 切应力 使单元体顺时针方向转动 为正；反之为负。  x'y'  yx  截面的方向角 xy 由x正向逆时针转到截面的 外法线n的正向的角为正; 反之为负。 n y x 

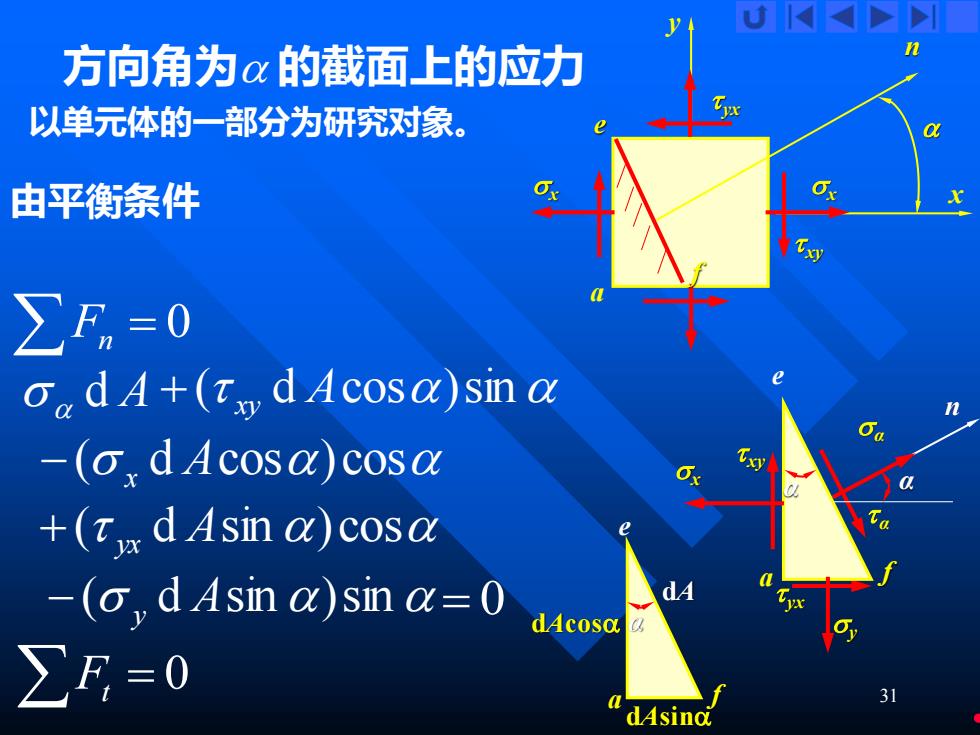
U K 方向角为α的截面上的应力 以单元体的一部分为研究对象。 由平衡条件 ∑Fn=0 odA+(dAcosa)sin a -(o,dAcosa)cosa +d Asin a)cosa -(o,d Asin a)sin a=0 dA ΣF=0 dAsina

31 方向角为 的截面上的应力 以单元体的一部分为研究对象。 由平衡条件 Fn = 0   d A + ( xy d Acos)sin  −( x d Acos)cos + ( yx d Asin )cos − ( y d Asin )sin  = 0 Ft = 0 x y a x x  yx  xy e f  n e a f x  xy  yx y α  α α n α e a f α dA dAsin dAcos