
关键是求出重心位置。现在利用制图软件可以方便求出: ·2.曲柄连杆机构中的惯性力 ·惯性力与运动质量有关,该机构中的运动质量有 ·往复运动质量 m,=m'+m1=m'+ 旋转运动质量 m,=mk+m2=mk+号m1 往复惯性 F,=-mj·a=-mjrw(cosa+元cos2a) C(cosa+Acos2a) Ccosa+AC cos2a =Fa+Fn ·往复惯性力的性质: ·a.j与a的变化规律相同,两者相差一个常数mj,方向相反。 ·b.可以用旋转矢量法确定FjI和jⅡ的大小、方向,用来判断往 复惯性力作用性质。 ·c.jI和jⅡ始终沿着气缸轴线作用。 ·d.往复惯性力总是存在。所以由j产生的单缸扭矩、翻倒力矩 和自由力总是存在。但是曲轴一转内,翻转力矩之和、自由力矩之 和为零。 旋转惯性力Fr
• 关键是求出重心位置。现在利用制图软件可以方便求出。 • 2. 曲柄连杆机构中的惯性力 • 惯性力与运动质量有关,该机构中的运动质量有 • 往复运动质量 旋转运动质量 往复惯性力 • 往复惯性力的性质: • a. Fj 与 a 的变化规律相同,两者相差一个常数 mj,方向相反。 • b. 可以用旋转矢量法确定 FjⅠ和 FjⅡ的大小、方向,用来判断往 复惯性力作用性质。 • c. FjⅠ和 FjⅡ 始终沿着气缸轴线作用。 • d. 往复惯性力总是存在。所以由 Fj 产生的单缸扭矩、翻倒力矩 和自由力总是存在。但是曲轴一转内,翻转力矩之和、自由力矩之 和为零。 • 旋转惯性力 Fr m l l mj = m + m = m + 2 1 m l l mr mk m mk = + = + 1 2 = + = + = + = − = − − + j j j j j F F C C C F m a m r cos cos 2 (cos cos 2 ) (cos cos 2 ) 2
F,mr ro2 (mg+m2)ra2 四、往复惯性力和气压力作用的差别 ·气压力Fg是做功的动力,产生输出扭矩。 ·气压力Fg在机体内部平衡,没有自由力。没有平衡,有自由 力产生,是发动机纵向振动的根源。 ·Fjmax<Fgmax ·j所占区域长,总是存在,正负面积相等:g呈脉冲性。 A-x 卫WT▣ a) b】 五、曲柄连杆机构中力的计算(动力计算) ·合成力 F=Fj+Fg ·侧向力 FN=F.tgB
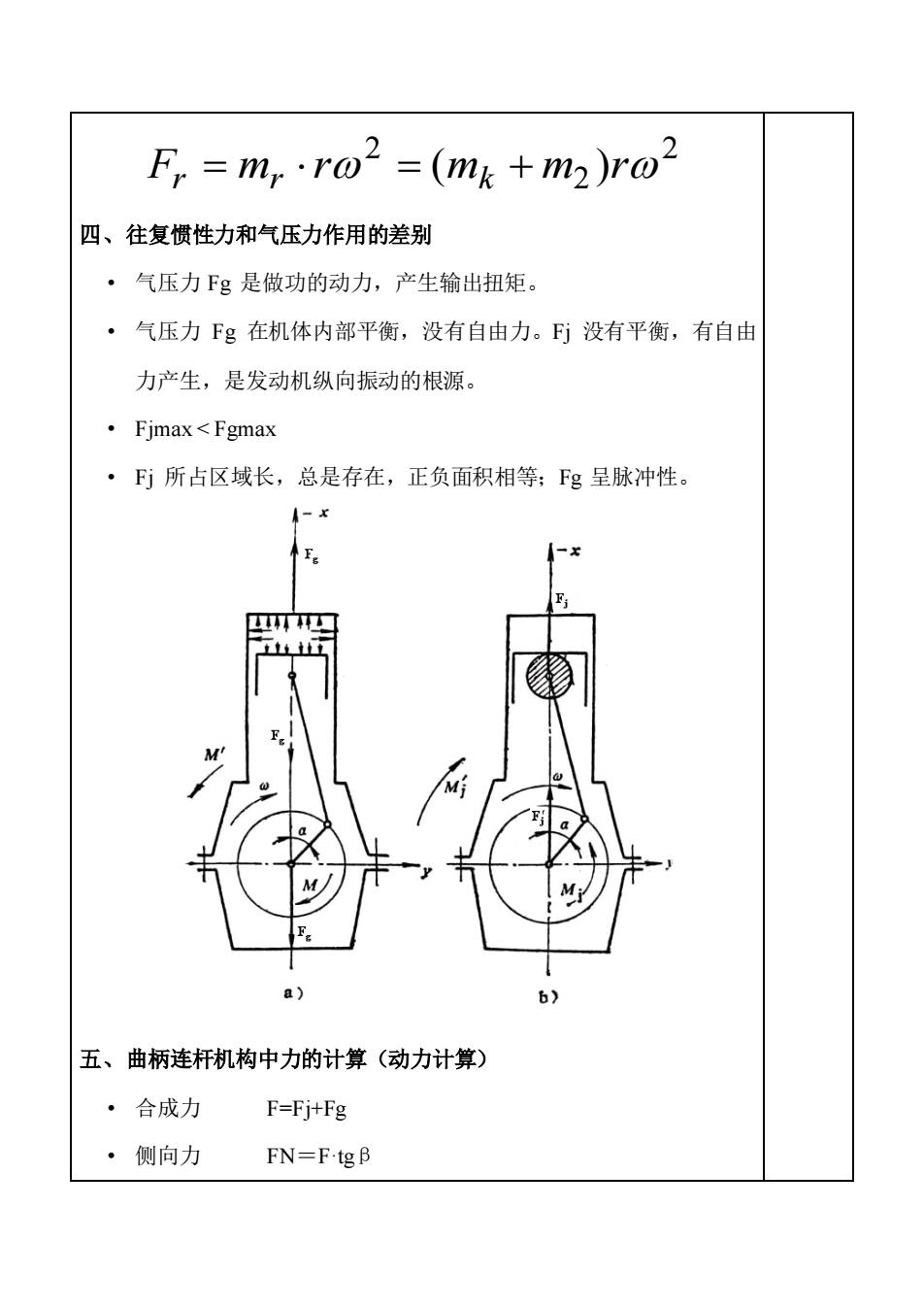
四、往复惯性力和气压力作用的差别 • 气压力 Fg 是做功的动力,产生输出扭矩。 • 气压力 Fg 在机体内部平衡,没有自由力。Fj 没有平衡,有自由 力产生,是发动机纵向振动的根源。 • Fjmax < Fgmax • Fj 所占区域长,总是存在,正负面积相等;Fg 呈脉冲性。 五、曲柄连杆机构中力的计算(动力计算) • 合成力 F=Fj+Fg • 侧向力 FN=F·tgβ 2 2 2 Fr = mr r = (mk + m )r
·连杆力 F= cos B 切向力 F=Fsin(a+B) ·径向力 Fk=Ficos(a+B) ·单缸扭矩 M=F·r·Ah ·翻倒力矩 M'=-M 六、多缸机扭矩(动力计算) 以六缸四行程发动机(1一5一3一6一2一4)为例:
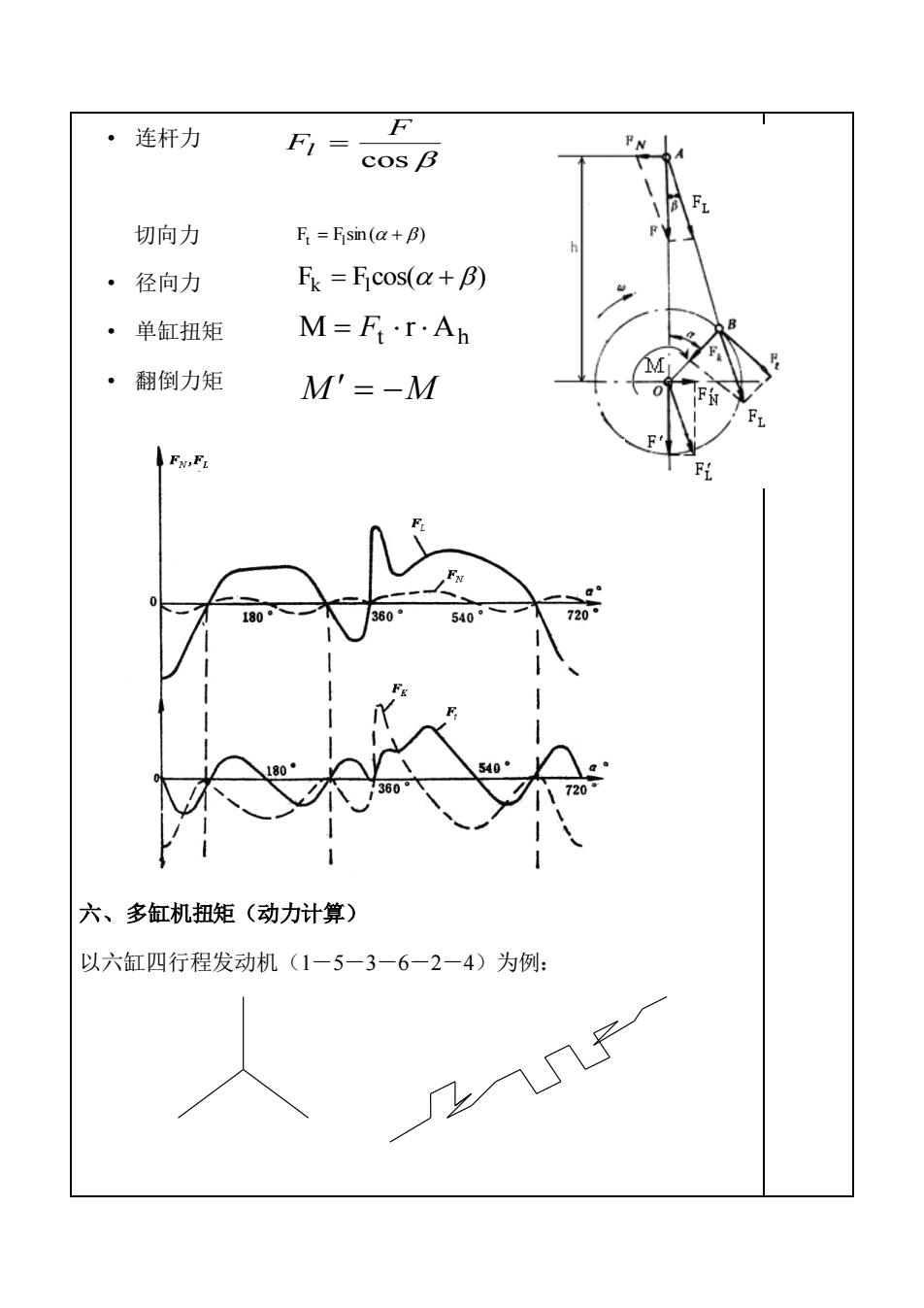
• 连杆力 切向力 • 径向力 • 单缸扭矩 • 翻倒力矩 六、多缸机扭矩(动力计算) 以六缸四行程发动机(1-5-3-6-2-4)为例: cos F Fl = F F sin ( ) t = l + F F cos( ) k = l + t Ah M = F r M = −M

如果第一缸的扭矩为M1(a),则第二缸的扭矩为M2=M1(a+240),MB =M1(a+480),. 第一主轴颈所受扭矩M0,1=0 第二主轴颈所受扭矩M1,2=M1(a) 第三主轴颈所受扭矩M2,3=M1,2+M1(a+240) 第四主轴颈所受扭矩M3,4=M2,3+M1(a+480) 第五主轴颈所受扭矩M4,5=M3,4+M1(a+120) 第六主轴颈所受扭矩M5,6=M4,5+M1(a+600) 第七主轴颈所受扭矩M6,7=M5,6+M1(a+360) 2.连杆轴颈扭矩 根据扭矩向后传递的原则,Mg应该是前一个主轴颈上的积累扭矩 M☑i与作用在本曲柄销上的切向力所引起单缸扭矩的一半。 M-号M,a@ Me=M2+5M,(a+240) =+如a+480) M=M+号M,(a+120) Ms=M"+号Ma+60) M=w“+Ma+30)
如果第一缸的扭矩为 M1(α),则第二缸的扭矩为 M2=M1(α+240),M3 =M1(α+480),. 第一主轴颈所受扭矩 M0,1=0 第二主轴颈所受扭矩 M1,2=M1(α) 第三主轴颈所受扭矩 M2,3= M1,2+M1(α+240) 第四主轴颈所受扭矩 M3,4= M2,3+ M1(α+480) 第五主轴颈所受扭矩 M4,5= M3,4+ M1(α+120) 第六主轴颈所受扭矩 M5,6= M4,5+ M1(α+600) 第七主轴颈所受扭矩 M6,7= M5,6+ M1(α+360) 2. 连杆轴颈扭矩 根据扭矩向后传递的原则,Mgi 应该是前一个主轴颈上的积累扭矩 Mzi 与作用在本曲柄销上的切向力所引起单缸扭矩的一半。 O 1,6 720° 5,2 3,4 120° 240° 360° 480° 600° 5 3 6 2 4 1 M0,1 M M 1,2 1 M2,3 M3,4 M2 M3 M4,5 M4 M5,6 M5 M6 M6,7 1 ( 360 ) 2 1 ( 600 ) 2 1 ( 120 ) 2 1 ( 480 ) 2 1 ( 240 ) 2 1 ( ) 2 1 2 1 6 5 4 3 2 1 = + + = + + = + + = + + = + + = = 1 5,6 1 4,5 1 3,4 1 2,3 1 1,2 1 M M M M M M M M M M M M M M M M M g g g g g g tr
3.平均扭矩 f∑Mda f∑Mda (∑M0m= C2-1 =5 4=720或360 A i 据此可以计算指示功率、有效扭矩等动力指标。 4.输出扭矩的均匀性 一般以标定工况评价扭矩不均匀系数 M= (∑M0mx-(∑M)mm (∑M)m 增加气缸数、点火均匀、组件分组、增加飞轮惯量等均可减小扭矩 不均匀性。 七、发动机对支承的作用力 W 91= F M 22b WF吲 M' 02= 22b 八、曲轴轴颈和轴承的负荷 1.连杆轴颈的负荷Pq Fq=FL+FrL
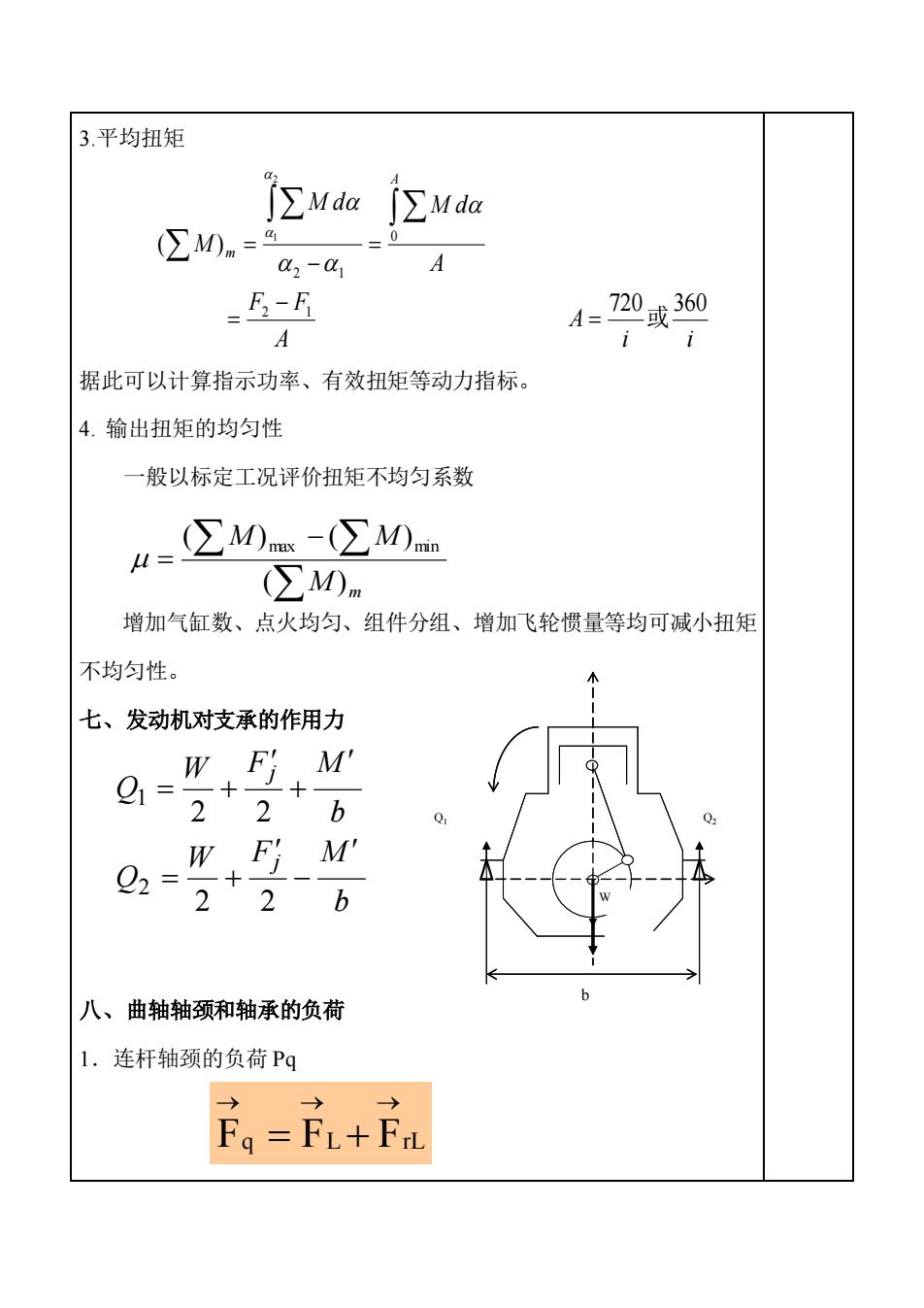
3.平均扭矩 据此可以计算指示功率、有效扭矩等动力指标。 4. 输出扭矩的均匀性 一般以标定工况评价扭矩不均匀系数 增加气缸数、点火均匀、组件分组、增加飞轮惯量等均可减小扭矩 不均匀性。 七、发动机对支承的作用力 八、曲轴轴颈和轴承的负荷 1.连杆轴颈的负荷 Pq i i A A F F A M d M d M A m 720 360 ( ) 2 1 0 2 1 2 1 = 或 − = = − = M m M M ( ) ( ) ( ) max min − = b W F M Q b W F M Q j j − = + + = + 2 2 2 2 2 1 b W Q1 Q2 b W Q1 Q2 Fq FL FrL → → → = +