
第五讲 正项级数及其审敛法
无 穷 级 数 第五讲 正项级数及其审敛法

无穷级数 1.正项级数的审敛性 00 定理1.(比值审敛法,达朗贝尔判别法)设 >1 n是正项级数 n=1 级数收敛 m+1 p<1, 若lim n o un =p,则{p=1 其它方法判别 p>1(或0),级数发散 定理2.(根值审敛法,柯西判别法)设 u,是正项级数, n=1 p<1, 级数收敛 若lim un=p,则{p=1, 其它方法判别· p>1(或∞), 级数发散
无 穷 级 数 1.正项级数的审敛性 定理1. (比值审敛法,达朗贝尔判别法) 定理2. (根值审敛法,柯西判别法)

无穷级数 举例 例1.判定下列级数的敛散性, 11, 1 1 1+i+12+123+.+ (m-1)! 解:因为 lim n+1二Lim (n-1)川 1 n→oo m n→0∞ n! lim=0 n→oo 根据比值判别法,级数收敛
无 穷 级 数 举例 例1. 判定下列级数的敛散性. 解: 根据比值判别法,级数收敛. 因为
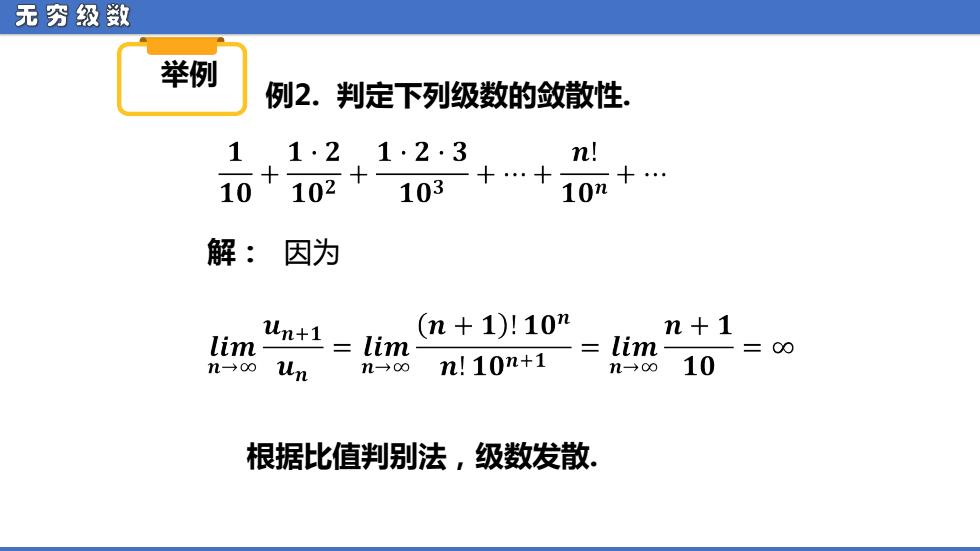
无穷级数 举例 例2.判定下列级数的敛散性 1,1·2,1·23 n! 10102 103+.+ 10n+. 解:因为 (n+1)!10n n+1 lim un+i lim lim =00 n→oo un n→o∞ n!10n+1 n→oo 10 根据比值判别法,级数发散
无 穷 级 数 举例 例2. 判定下列级数的敛散性. 解: 因为 根据比值判别法,级数发散
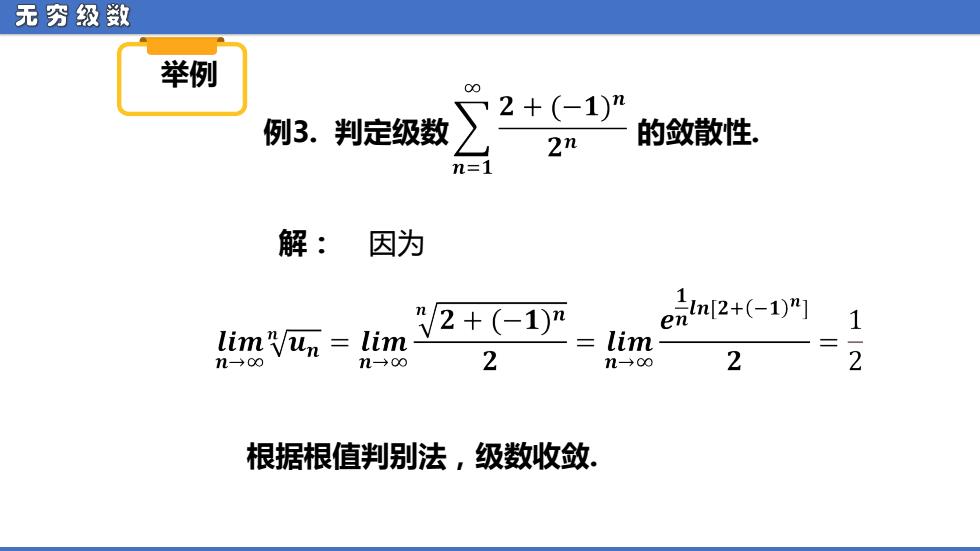
无穷级数 举例 00 2+(-1)” 例3.判定级数 2n 的敛散性, n=1 解:因为 V2+-1)m m2+(-1)"] en 7 limun lim lim n→00 2 n→oo 2 -2 根据根值判别法,级数收敛
无 穷 级 数 举例 例3. 判定级数 的敛散性. 解: 因为 根据根值判别法,级数收敛