
第三讲 幂级数习题
无 穷 级 数 第三讲 幂 级 数 习题
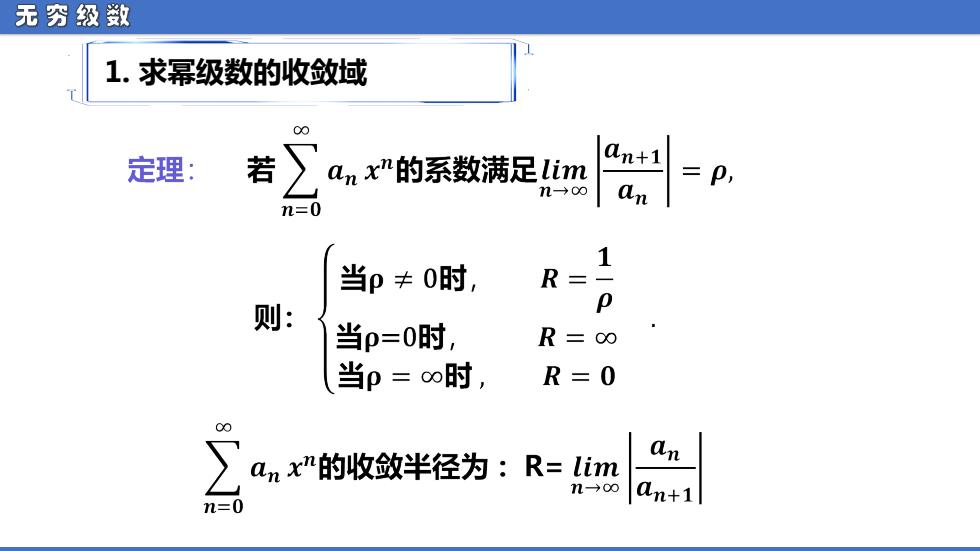
无穷级敛 1.求幂级数的收敛域 00 定理: 若)anx"的系数满足Lim An+1 =P, n→∞ an n=0 1 当p≠0时, R= 则: 当p=0时, R=0∞ 当p=o时, R=0 00 anx的收敛半径为:R=lim an n-→0∞ n=0 an+i
无 穷 级 数 1. 求幂级数的收敛域

无穷级数 00 举例 x2n+1 例1.求幂级数(-1)” 2n+1 的收敛半径及收敛域: n=1 解:因为 (2n+1)x2n+3 2n+1 lim (2n+3)x2n+1 lim n→oo n→0∞ B+1w1 当x=一1时级数 (-1)n+1 收敛, 2n+1 n=1 当x=1时,级数 〉,(-1m-1 收敛, n1 原级数的收敛半径为1,收敛域为[-1,1]
无 穷 级 数 举例 例1. 求幂级数 解: 因为 原级数的收敛半径为1,收敛域为[-1,1]

无穷级数 举例 (x-5)m 例2.求幂级数 的收敛区间及收敛域, Vn n=0 (x-5)+1Vm 解:因为lim <1,→1(x-5)川<1, vn+1(x-5)n 4<x<6. 当x=4时级数 -1)” 收敛, n=0 00 当x=6时,级数 发散 原级数的收敛区间为(4,6),收敛域为4,6)
无 穷 级 数 举例 例2. 求幂级数 解: 因为 ᵽ < ᵉ < ᵽ

无穷级数 举例 例3.求幂级数 xn的收敛区间 n< 解:因为 lim n→0∞ =ex<1解得: -1<x<l e e 原级数的收敛区间为(-己君·
无 穷 级 数 举例 例3. 求幂级数 解: 因为 − ᵼ ᵈ < ᵉ < ᵼ ᵈ