
3.3直方图处理 >直方图: 956 h(rk)=nk 其中:k∈[O,L-1]一一灰度级;nk-灰度级为rk的像素个数 >归-化直方图:-)=,0≤,≤1%=01.2L-1 ∑2opr(m)=1,n为像素总数 (k)原始图像灰度分布的概率密度函数 如果将r归一化到[01]之间,则r可以看作区间[01] 的随机变量
3.3 直方图处理 直方图: ℎ(𝑟𝑟𝑘𝑘) = 𝑛𝑛𝑘𝑘 其中:𝑟𝑟𝑘𝑘 ∈ [0, 𝐿𝐿 − 1]—— 灰度级;𝑛𝑛𝑘𝑘 − 灰度级为𝑟𝑟𝑘𝑘的像素个数 归一化直方图:𝑝𝑝𝑟𝑟(𝑟𝑟𝑘𝑘) = 𝑛𝑛𝑘𝑘 𝑛𝑛 , 0 ≤ 𝑝𝑝𝑟𝑟 ≤ 1, 𝑟𝑟𝑘𝑘 = 0,1,2, . . . 𝐿𝐿 − 1 ∑𝑟𝑟𝑘𝑘=0 𝐿𝐿−1 𝑝𝑝𝑟𝑟(𝑟𝑟𝑘𝑘) = 1,n为像素总数 𝑝𝑝𝑟𝑟 𝑟𝑟𝑘𝑘 原始图像灰度分布的概率密度函数 如果将rk归一化到[0 1]之间,则rk可以看作区间[0 1] 的随机变量

3.3.1 直方图均衡化 >直方图均衡化处理: 假设原图的灰度值变量为r,变换后新图的灰度值变量 为s,我们希望寻找一个灰度变换函数T:s=T(r), 使得概率密度函数p,(r)变换成希望的概率密度函数 Ps(s) >灰度变换函数T()应该满足: (1) T(r)在区间[0,1]中单调递增且单值; (2) r∈[0,1],有T(r)∈[0,1]:
3.3.1 直方图均衡化 直方图均衡化处理: 假设原图的灰度值变量为r,变换后新图的灰度值变量 为s,我们希望寻找一个灰度变换函数T:s=T(r), 使得概率密度函数pr(r)变换成希望的概率密度函数 ps(s) 灰度变换函数T(r)应该满足: (1) 𝑇𝑇(𝑟𝑟)在区间[0 , 1]中单调递增且单值; (2) ∀𝑟𝑟 ∈ [0 , 1],有𝑇𝑇(𝑟𝑟) ∈ [0 , 1];

>满足以上条件的一个重要的直方图均衡化 的灰度变换函数为 k s=)= p(rk)dr(3.3-4) 原始图象灰度r的累积分布函数(CDF) 1 可以证明 ps(s)= 一1均匀分布的 对于数字图象: (3.3.8)k=0,1,2,…,L-1 i=0 随机变量:不一定是均匀分布的 根据该方程可以由原图像的各像素灰度值直接得 到直方图均衡化后各灰度级所占的百分比
满足以上条件的一个重要的直方图均衡化 的灰度变换函数为 𝑠𝑠 = 𝑇𝑇(𝑟𝑟𝑘𝑘) = � 0 𝑟𝑟𝑘𝑘 𝑝𝑝𝑟𝑟(𝑟𝑟𝑘𝑘)𝑑𝑑𝑑𝑑 (3.3 − 4) 原始图象灰度r的累积分布函数(CDF) 对于数字图象: 𝑠𝑠𝑘𝑘 = 𝑇𝑇(𝑟𝑟𝑘𝑘) = � 𝑗𝑗=0 𝑘𝑘 𝑝𝑝𝑟𝑟(𝑟𝑟𝑗𝑗) = � 𝑗𝑗=0 𝑘𝑘 𝑛𝑛𝑗𝑗 𝑛𝑛 (3.3.8) 𝑘𝑘 = 0,1,2, ⋯ , 𝐿𝐿 − 1 根据该方程可以由原图像的各像素灰度值直接得 到直方图均衡化后各灰度级所占的百分比 随机变量:不一定是均匀分布的 𝑝𝑝𝑠𝑠 𝑠𝑠 = 均匀分布的 1 𝐿𝐿 − 1 可以证明

>直方图均衡化处理的计算步骤如下: 956 (1)统计原始图象的直方图 Pr(Tk)= k是输入图象灰度级; (2)计算直方图累积分布曲线 n (3)用累积分布函数作变换函数计算图像变换后的灰度级 S(k)≈(L-1)*Sk (4)建立输入图象与输出图象灰度级之间的对应关系, 变换后灰度级范围应该和原来的范围一致
直方图均衡化处理的计算步骤如下: (1)统计原始图象的直方图 是输入图象灰度级; (2)计算直方图累积分布曲线 (3)用累积分布函数作变换函数计算图像变换后的灰度级 (4)建立输入图象与输出图象灰度级之间的对应关系, 变换后灰度级范围应该和原来的范围一致。 𝑝𝑝𝑟𝑟 𝑟𝑟𝑘𝑘 = 𝑛𝑛𝑘𝑘 𝑛𝑛 𝑟𝑟𝑘𝑘 𝑠𝑠𝑘𝑘 = 𝑇𝑇(𝑟𝑟𝑘𝑘) = � 𝑗𝑗=0 𝑘𝑘 𝑝𝑝𝑟𝑟(𝑟𝑟𝑗𝑗) = � 𝑗𝑗=0 𝑘𝑘 𝑛𝑛𝑗𝑗 𝑛𝑛
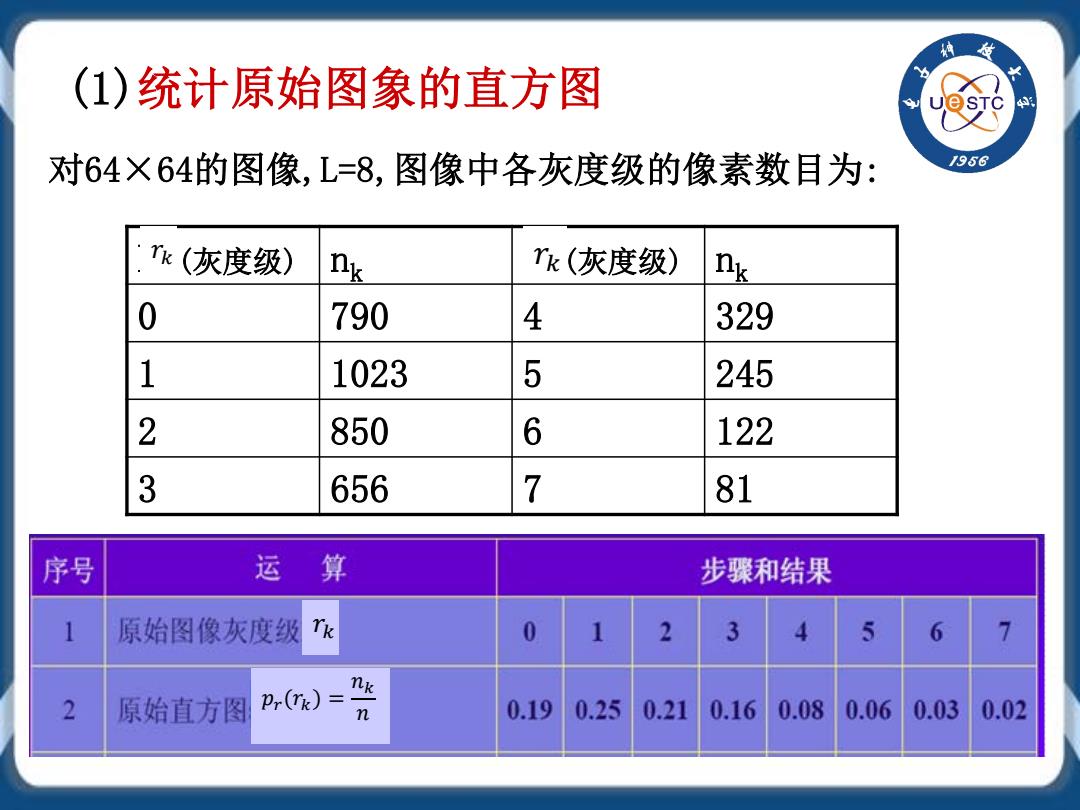
(1)统计原始图象的直方图 4 对64×64的图像,L=8,图像中各灰度级的像素数目为: 956 rk(灰度级) nk Tk(灰度级) nk 0 790 4 329 1 1023 5 245 2 850 6 122 3 656 7 81 序号 运算 步骤和结果 1 原始图像灰度级k 0 1 2 3 5 6 2 原始直方图 p,)= 0.19 0.25 0.21 0.16 0.08 0.06 0.03 0.02
对64×64的图像,L=8,图像中各灰度级的像素数目为: K (灰度级) nk k (灰度级) nk 0 790 4 329 1 1023 5 245 2 850 6 122 3 656 7 81 𝑟𝑟𝑘𝑘 𝑟𝑟𝑘𝑘 pr 𝑟𝑟𝑘𝑘 𝑝𝑝𝑟𝑟(𝑟𝑟𝑘𝑘) = 𝑛𝑛𝑘𝑘 𝑛𝑛 (1)统计原始图象的直方图