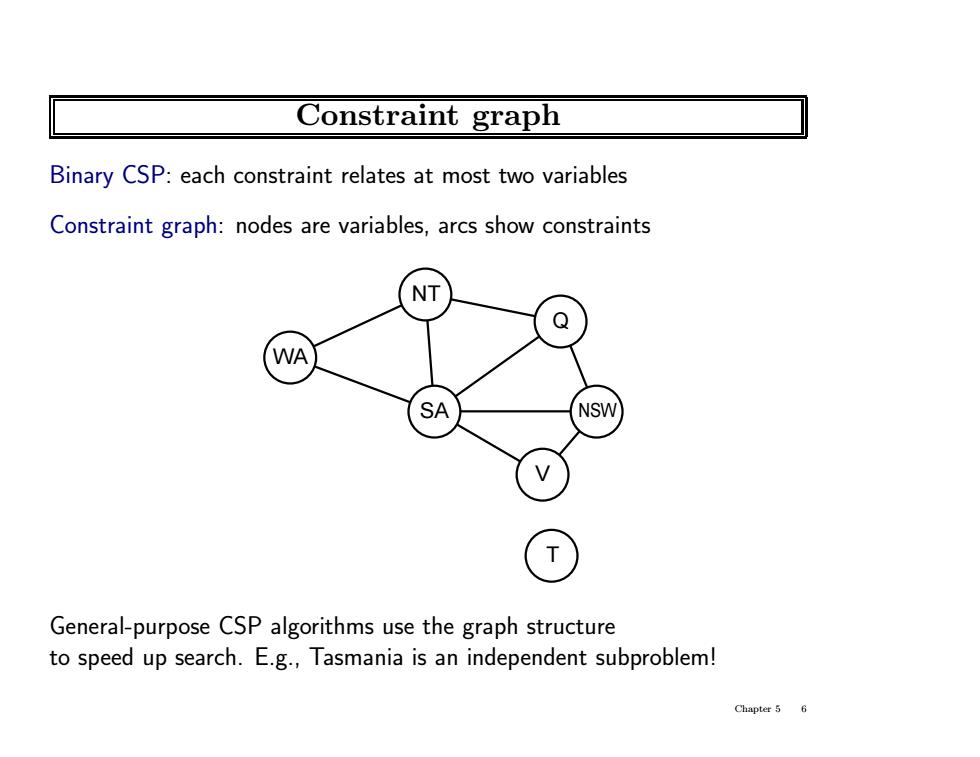
Constraint graph Binary CSP:each constraint relates at most two variables Constraint graph:nodes are variables,arcs show constraints NT WA SA NSW General-purpose CSP algorithms use the graph structure to speed up search.E.g.,Tasmania is an independent subproblem! Chapter 5 6
Constraint graph Binary CSP: each constraint relates at most two variables Constraint graph: nodes are variables, arcs show constraints Victoria WA NT SA Q NSW V T General-purpose CSP algorithms use the graph structure to speed up search. E.g., Tasmania is an independent subproblem! Chapter 5 6

Varieties of CSPs Discrete variables finite domains;size d=O(d")complete assignments e.g.,Boolean CSPs,incl.Boolean satisfiability (NP-complete) infinite domains (integers,strings,etc.) e.g.,job scheduling,variables are start/end days for each job need a constraint language,e.g.,StartJob1+5<Start.Jobs linear constraints solvable,nonlinear undecidable Continuous variables e.g.,start/end times for Hubble Telescope observations linear constraints solvable in poly time by LP methods Chapter 5 7
Varieties of CSPs Discrete variables finite domains; size d ⇒ O(dn) complete assignments ♦ e.g., Boolean CSPs, incl. Boolean satisfiability (NP-complete) infinite domains (integers, strings, etc.) ♦ e.g., job scheduling, variables are start/end days for each job ♦ need a constraint language, e.g., StartJob1 + 5 ≤ StartJob3 ♦ linear constraints solvable, nonlinear undecidable Continuous variables ♦ e.g., start/end times for Hubble Telescope observations ♦ linear constraints solvable in poly time by LP methods Chapter 5 7

Varieties of constraints Unary constraints involve a single variable, e.g,SA卡green Binary constraints involve pairs of variables, e.g,SA≠WA Higher-order constraints involve 3 or more variables, e.g.,cryptarithmetic column constraints Preferences(soft constraints),e.g.,red is better than green often representable by a cost for each variable assignment constrained optimization problems Chapter 5 8
Varieties of constraints Unary constraints involve a single variable, e.g., SA 6= green Binary constraints involve pairs of variables, e.g., SA 6= WA Higher-order constraints involve 3 or more variables, e.g., cryptarithmetic column constraints Preferences (soft constraints), e.g., red is better than green often representable by a cost for each variable assignment → constrained optimization problems Chapter 5 8
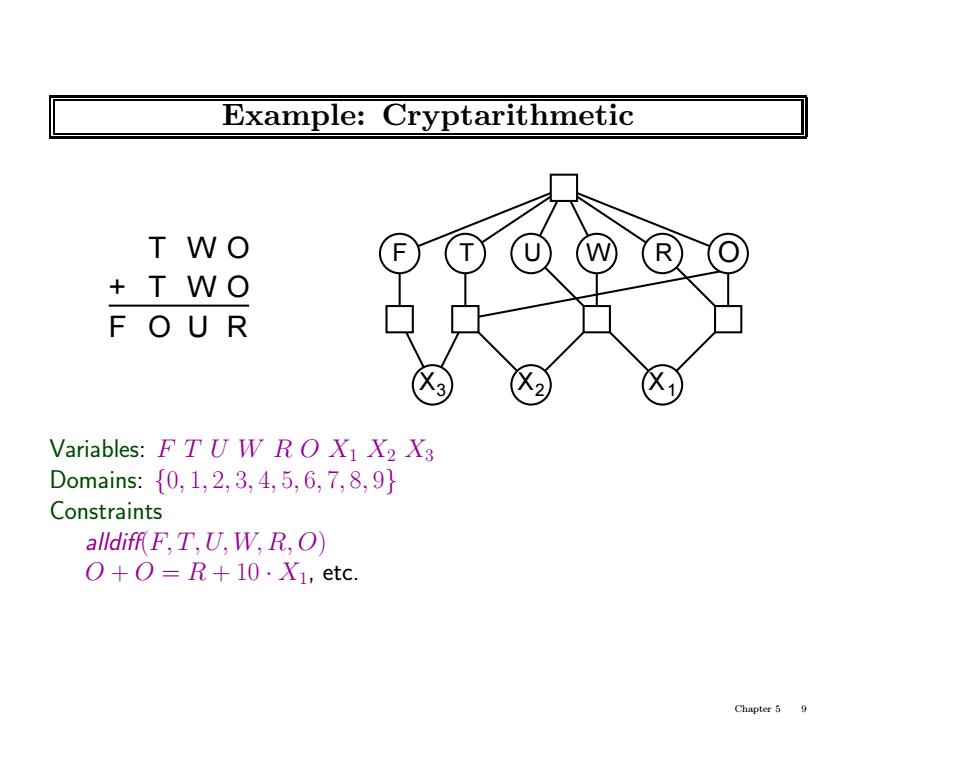
Example:Cryptarithmetic T WO R +T WO FOUR 2 Variables:F TU W RO X1 X2 X3 Domains:{0,1,2,3,4,5,6,7,8,9} Constraints alldiff F,T,U,W,R,O) O+O=R+10·X1,etc. Chapter 59
Example: Cryptarithmetic F T U W R O + T W O T W O F O U R X3 X2 X1 Variables: F T U W R O X1 X2 X3 Domains: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Constraints alldiff(F, T,U, W, R, O) O + O = R + 10 · X1, etc. Chapter 5 9

Real-world CSPs Assignment problems e.g.,who teaches what class Timetabling problems e.g.,which class is offered when and where? Hardware configuration Spreadsheets Transportation scheduling Factory scheduling Floorplanning Notice that many real-world problems involve real-valued variables Chapter 5 10
Real-world CSPs Assignment problems e.g., who teaches what class Timetabling problems e.g., which class is offered when and where? Hardware configuration Spreadsheets Transportation scheduling Factory scheduling Floorplanning Notice that many real-world problems involve real-valued variables Chapter 5 10