
11 黑體幅射的頻譜無法以古典物理(如熱力學或雷磁學)來解釋 (1)Wien's Law 利用熱力學推導得出 I() 實驗值 →在長波長處與實驗結果不和 Raleigh-Jeans Law (2)Rayleigh-Jeans Law 利用電磁學理論及能量均分定 Wien's Law 理推導得出 →在短波長處與實驗結果不和 UV catastrophe T=1646k 入 交源大孽李威熊 2012物理是想
11 交通大學 李威儀 2012 物理異想 黑體幅射的頻譜無法以古典物理 ( 如熱力學或電磁學 ) 來解釋 (1) Wien’s Law : 利用熱力學推導得出 在長波長處與實驗結果不和 (2) Rayleigh-Jeans Law : 利用電磁學理論及能量均分定 理推導得出 在短波長處與實驗結果不和 ( UV catastrophe ) Raleigh-Jeans Law Wien’s Law T=1646k I (l) l 實驗值

12 浦朗克的理論(Planck's Theory)-1900 (1)Treat blackbody as large number of atomic oscillators simple harmonic oscillator )each of which emits and absorbs EM waves (2)Each atomic oscillator can have only discrete values of energy E=nhu,n=0,1,2,.. h=6.63x10-34Js←浦朗克常數(Planck's constant) (3)The energy of the EM wave emitted by the atomic oscillators must be in multiples of hu 能量令 三 連續變化的能量 不連續變化 Planck (量子化)的能量 Max Planck (1858-1947 1918諾貝爾獎得声大城機 2012物理果源
12 交通大學 李威儀 2012 物理異想 浦朗克的理論 ( Planck’s Theory ) - 1900 (1) Treat blackbody as large number of atomic oscillators ( simple harmonic oscillator ), each of which emits and absorbs EM waves (2) Each atomic oscillator can have only discrete values of energy E = n hu , n = 0, 1, 2, … h = 6.63 x 10-34 J•s 浦朗克常數 ( Planck’s constant ) (3) The energy of the EM wave emitted by the atomic oscillators must be in multiples of hu Max Planck (1858 – 1947 ) 1918 諾貝爾獎得主 連續變化的能量 不連續變化 (量子化) 的能量 能 量 hu

13 黑體幅射的頻譜無法以古典物理(如熱力學或電磁學)來解釋 但Planck's Theory卻能推導出與實驗完全穩合的結果! Planck's (1)Wien's Law Theory 利用熱力學推導得出 1() 實驗值 →在長波長處與實驗結果不和 Raleigh-Jeans Law (2)Rayleigh-Jeans Law 利用電磁學理論及能量均分定 Wien's Law 理推導得出 )在短波長處與實驗結果不和 UV catastrophe T=1646k 入 (浦朗克常數就是浦朗克在嘗試將理論曲線 與實驗曲線一致化的過程中反推得到的數值) 交源大孽李威熊 2012物理果源
13 交通大學 李威儀 2012 物理異想 Raleigh-Jeans Law Wien’s Law T=1646k 黑體幅射的頻譜無法以古典物理 ( 如熱力學或電磁學 ) 來解釋 但Planck’s Theory 卻能推導出與實驗完全穩合的結果 ! I (l) l 實驗值 (1) Wien’s Law : 利用熱力學推導得出 在長波長處與實驗結果不和 (2) Rayleigh-Jeans Law : 利用電磁學理論及能量均分定 理推導得出 在短波長處與實驗結果不和 ( UV catastrophe ) Planck’s Theory ( 浦朗克常數 就是浦朗克在嘗試將理論曲線 與實驗曲線一致化的過程中反推得到的數值 )

14 Planck's model>EM energy absorbed/emitted as a collection of discrete amount or packets of energy with each packet equals to hu →電磁波能量可以被量子化(quantized)?(也就是做不連續性的變化) →電磁波具有粒子的特性?:此時尚未有此觀念! 為什麼平常在觀察簡諧振盪時沒有觀察到能量量子化的現象? 例: m=10 kg attached to a spring spring constant,k=103 N/m initial amplitude,A=0.1 m →E=2kA2=2X103x(0.1)2=5J →0=112元(k/m)12=1.59Hz separation between adjacent energy level △E=h0=6.63x1034×1.59=10-33J 量子化的效應很難被觀察到!(正因為h非常的小,古典物理才沒發現 交源大擎李威熊 2012物理果源
14 交通大學 李威儀 2012 物理異想 例 : m = 10 kg attached to a spring spring constant, k = 103 N/m initial amplitude, A = 0.1 m E = ½ k A2 = ½ x 103 x (0.1)2 = 5 J u = 1/2p ( k/m )1/2 = 1.59 Hz separation between adjacent energy level : DE = hu = 6.63 x 10-34 x 1.59 = 10-33 J 量子化的效應很難被觀察到 ! ( 正因為 h 非常的小,古典物理才沒發現它 ! ) Planck’s model EM energy absorbed/emitted as a collection of discrete amount or packets of energy , with each packet equals to hu 電磁波能量可以被量子化 ( quantized ) ? ( 也就是做不連續性的變化 ) 電磁波具有粒子的特性 ? : 此時尚未有此觀念 ! 為什麼平常在觀察簡諧振盪時沒有觀察到能量量子化的現象 ?
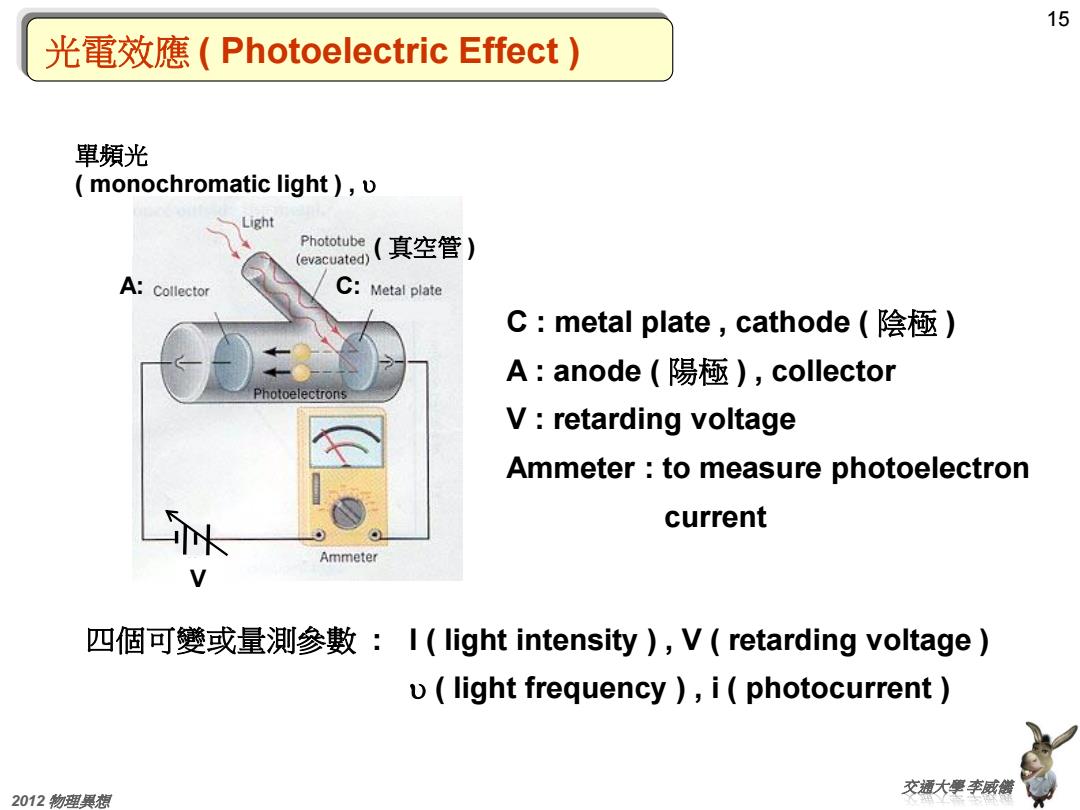
15 光電效應(Photoelectric Effect) 單頻光 monochromatic light )v Light Phototube(真空管) (evacuated) A:Collector C:Metal plate C:metal plate,cathode(陰極) A:anode(陽極),collector Photoelectrons V:retarding voltage Ammeter:to measure photoelectron current Ammeter 四個可變或量测參數:I(light intensity),V(retarding voltage) u(light frequency )i(photocurrent 交源大孽李威熊 2012物理果想
15 交通大學 李威儀 2012 物理異想 光電效應 ( Photoelectric Effect ) C : metal plate , cathode ( 陰極 ) A : anode ( 陽極 ) , collector V : retarding voltage Ammeter : to measure photoelectron current 四個可變或量測參數 : I ( light intensity ) , V ( retarding voltage ) u ( light frequency ) , i ( photocurrent ) A: C: 單頻光 ( monochromatic light ) , u ( 真空管 ) V