
异或连接词(Exclusive Disjunction,XOR) ·p⊕q:“要么p,要么q,但非pAq” 例子: 。 张晓静不是江西人就是 P q p⊕q 安徽人 F F F ·套餐:鸡腿饭或者叉烧 T T 饭,苹果或香蕉 入 F T T p⊕q=(pVq)∧(p∧q) p⊕q=(p∧q)V(-p∧q)
异或连接词(Exclusive Disjunction, XOR) • 𝑝⨁𝑞:“要么p,要么q,但非𝑝 ∧ 𝑞” P q 𝑝⨁𝑞 F F F F T T T F T T T F 例子: • 张晓静不是江西人就是 安徽人 • 套餐:鸡腿饭或者叉烧 饭,苹果或香蕉
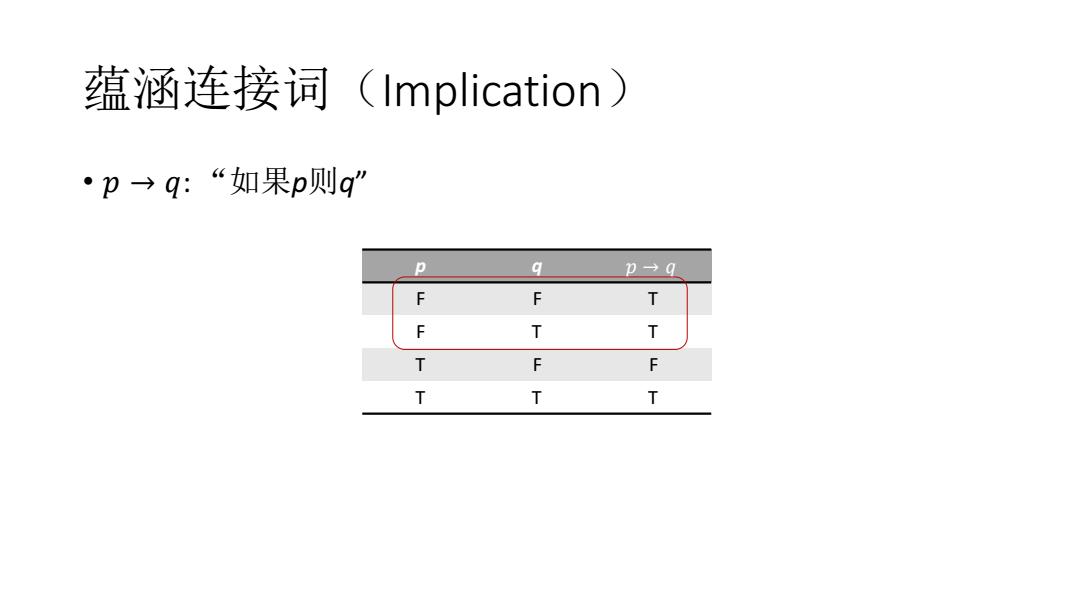
蕴涵连接词(Implication) ·卫→q:“如果p则q” p 9 p→q F F T F T T T F F T 下 入
蕴涵连接词(Implication) • 𝑝 → 𝑞: “如果p则q” p q 𝑝 → 𝑞 F F T F T T T F F T T T
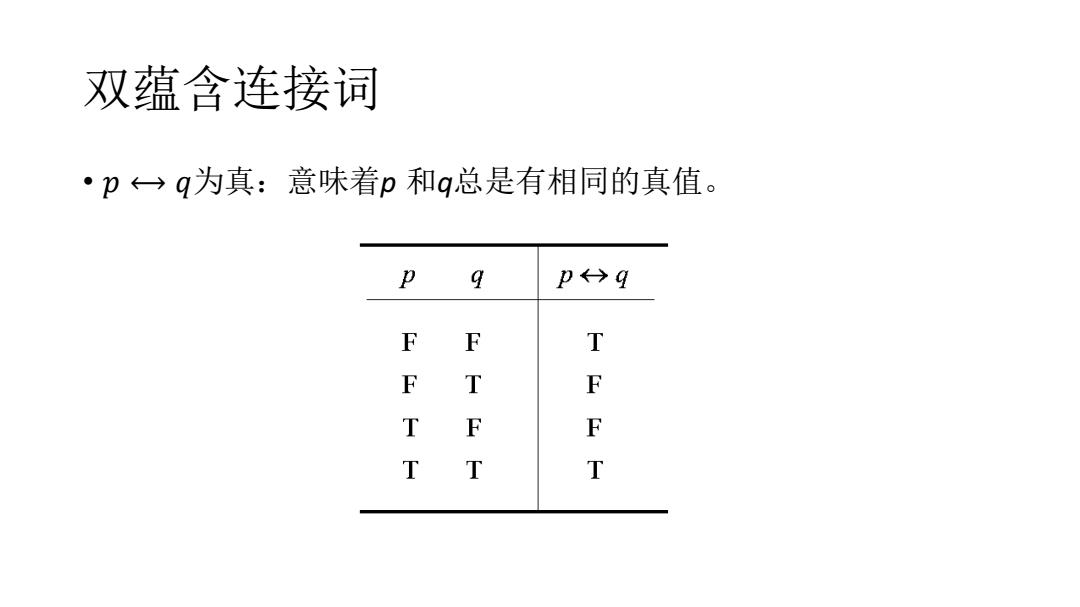
双蕴含连接词 ·p←→q为真:意味着p和q总是有相同的真值。 9 卫←→q F F T F T F T F F T T T
双蕴含连接词 • 𝑝 ⟷ 𝑞为真:意味着p 和q总是有相同的真值

自然语言与逻辑中的连接词 ·不是。。。 并且。。。 ·每个连接词与我们日常生活中 或者。。。 ·V 的某个连接词大致对应,但只 ·不是。。。就是。 是“大致”对应。 。⊕ ·如果。。。那么。。。 ·对连接词的理解和使用严格按 ·当且仅当 。← 照真值表给出的“数学定义
自然语言与逻辑中的连接词 • 不是。。。 • 。。。并且。。。 • 。。。或者。。。 • 不是。。。就是。。。 • 如果。。。那么。。。 • 当且仅当 • 每个连接词与我们日常生活中 的某个连接词大致对应,但只 是“大致”对应。 • 对连接词的理解和使用严格按 照真值表给出的“数学定义” • ¬ • ∧ • ∨ • ⨁ • ⟶ • ⟷