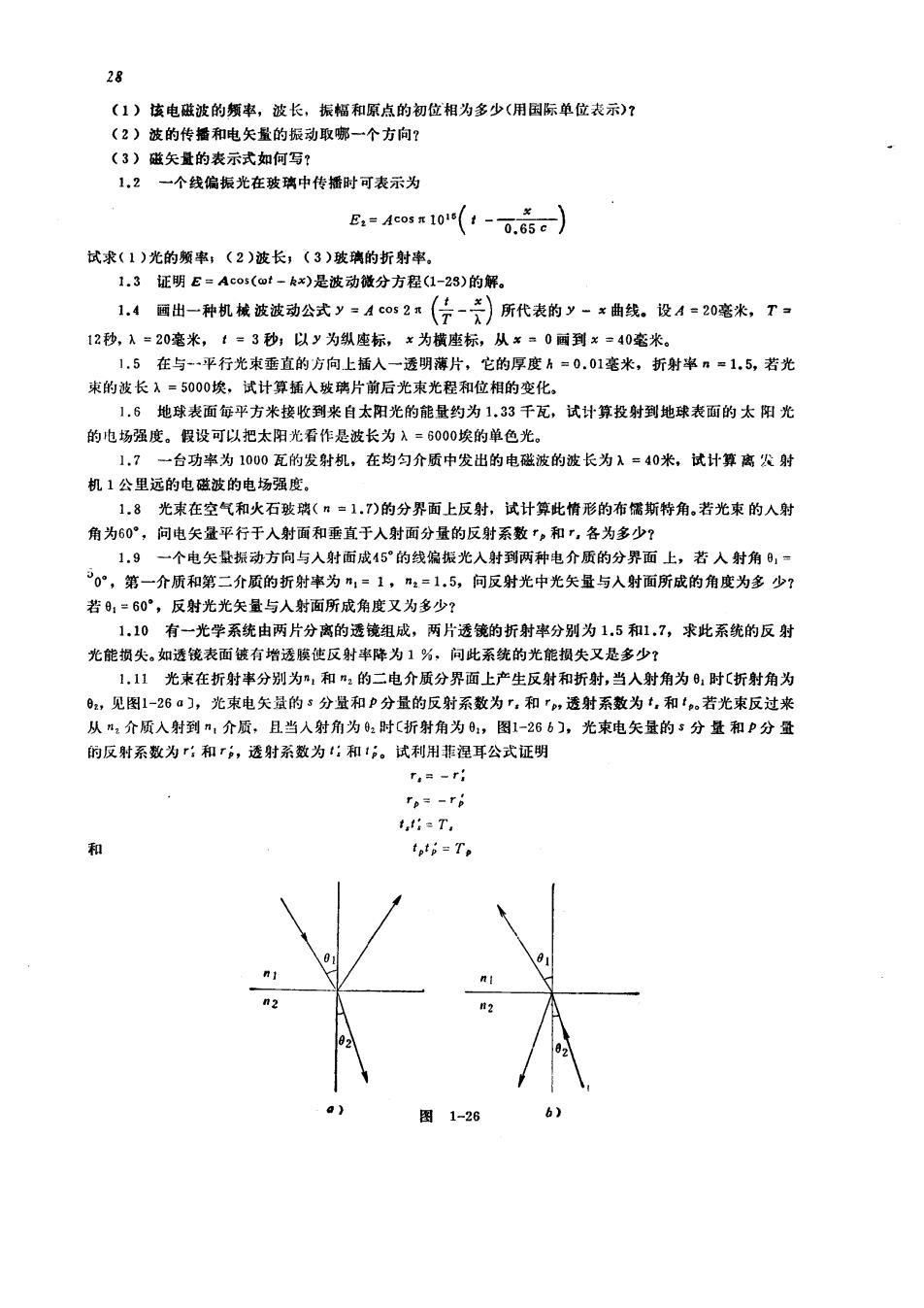
(1)该电监被的频市,波长,振幅和原点的初位相为多少(用国际单位表示)? (2)波的传播和电矢量的振动取哪一个方向? (3)磁矢量的表示式如何写? 1.2 一个线偏振光在玻璃中传插时可表示为 B=4eosn10…(:-。.点g) 试求(1)光的颜事;(2)波长,(3)玻璃的折射率。 1.3证明E=Aco5(@t-kx)是波动微分方程1-23)的解。 1,4画出一种机械波波动公式y=Ac052m(行-)所代表的y-x曲线。设A=20毫米,T一 2秒,人20毫米,3秒;以y为纵座标,为横座标,从¥。0到×=40毫米。 1,5在与…平行光束垂直的方向上插入一透明薄片,它的厚度片=0.01毫米,折射率n。1.5,若光 束的被长入=5000埃。试计算插入玻璃片前后光束光程和位相的变化。 1,5地球表面每平方米接收到来自太阳光的能量约为1,33千瓦,试计算投射到地球表面的太阳光 的九场强度。假设可以把太阳光香作是波长为入=6000埃的单色光。 一台功率为100瓦的发射机,在均匀介质中发出的电磁波的波长为入=40米,试计算离发射 机1公里远的电磁被的电场强度, 1,8光束在空气和火石玻胰(#=1.)的分界面上反射,试计算此情形的布儒斯特角,若光束的人射 角为60°,问电失量平行于人射面和垂直于人射面分量的反射系数,和,各为多少? 1.9一个电矢量振动方向与入射面成45°的线偏振光入射到两种电介质的分界面上,若入射角,一 0°,第一介质和第二介质的折射率为州=1,m=1,5,向反射光中光矢量与人射面所成的角度为多少? 若=60,反射光光关 量与人射面所成角度又为多少 1.10有一光学系统由两片分离的透镜组成,两片透镜的折射率分别为1.5和1,7,求此系统的反射 光能损失如透镜表面镀有增透膜使反射率降为1%,问此系统的光能损失又是多少? 1.11光束在折射率分别为,和m:的二电介质分界面上产生反射和折射,当人射角为:时(折射角为 ,见图1-26,光束电矢量的5分量和P分量的反射系数为,和,透射系数为,和,若光束反过来 从,介质入射到n,介质,且当人射角为时折射角为: ,图1-266们,光桌电失量的:分量和P分量 的反射系数为和,透射系数为:和:。试利用非混耳公式证明 r,周-f: r。a-r =T
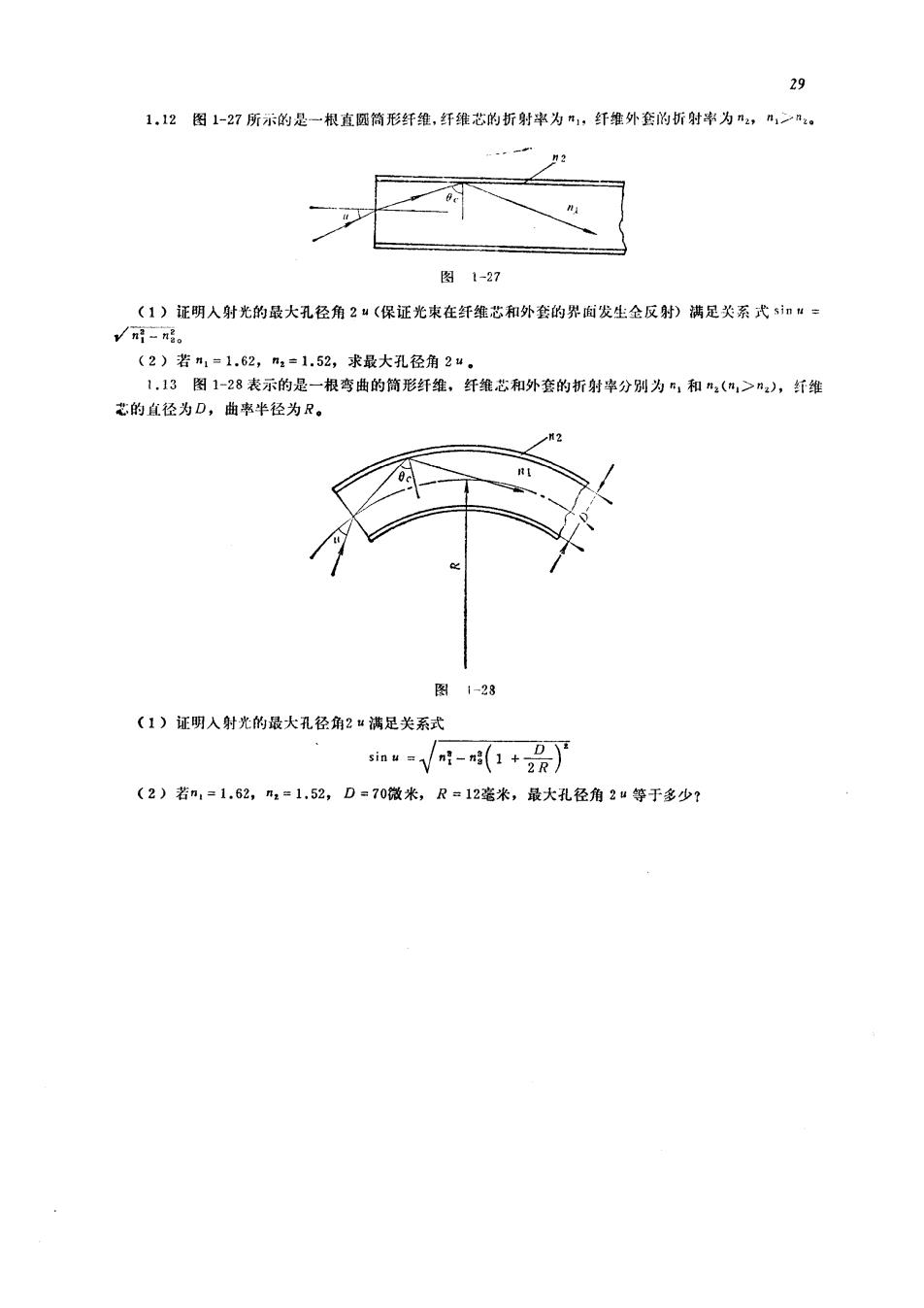
29 1.12图1-27所示的是一根直圆形纤维,纤维花的折射率为,纤维外套的析射率为2,之。 图1-27 (1)证明人射光的最大孔径角2:(保证光束在纤维艺和外套的界面发生金反射)满足关系式sn”= √-。 《2)若m1=1.62,m=1.52,求最大孔径角2“。 图1-28表示的是一根弯曲的筒形纤维,纤维芯和外套的折射率分别为和(>n,钉维 艺的直径为D,曲淑半径为R。 图1-28 (1)证明人射光的最大孔径角2“满足关系式 ia√好-(1+0) (2)若m,=1.62,=1,52,D=70微米,R12毫米,最大孔径角2#等于多少

第二章光波的迭加与分析 两个(或多个)光波在空间某一区域相避时,发生光波的迭加问题。一般说来,颜率、 振幅和位相都不相同的光被的选加,情形是很复杂的。这里,只限于讨论颜率相同或颜率相 差很小的单色光被的迭加,在这种情况下,可写出结果的数学表示式。尽管实际光源发出 的光波不能认为是余弦函数或正弦函数表示的单色光波,但是我们将会看到任何复杂的波刻 都可以分解为一组由余弦函数和正弦函数表示的单色波之和,因此论单色光波有着实际意 义。 波的逃服从达加原理,这个原理可以表述为:几个波在相遇点产生的合振动是各个 被单独产:生的振动的矢量和。迭加原理实质上是表示波传播的独立性,也就是说,每一个波 独立地产生作用,这种作用不因其他波的存在而受到影响。日常生活中有许多现象都可以说 明光波或任何其他波动传播的独立性,譬如两个光波在相遇之后又分开,而每一个光波仍保 持原有的特性(频率、波长、振动方向等)按照自己的传播方向继续前进,好象在各自的路 程上并未過到其他光波一样。另一方面,迭加原理也是介质对光波的线性响应的一种反映, 但这只是当光被的强度较低时是正确的,而当光波的强度很大时(例如电场强度高达10伏/来 的微光),将产生非线性效应,这时介质对光波的响应是非线性的(见§8-10),上述线性迭 加原理不耳适用。 光波的分析要利用数学上的两个定理:傅里叶级数定理和傅里叶积分定理。有关这两个 定理的数学内容可参阅附录【,这两个定理也是傅里叶光学(第五章)的数学基础,读者必 须熟练学握。 §2-1两个频率相同、振动方向相同的单色光波的迭加 如图?-1所示,设两个频*相同,振动方向相同(同在y方向)的单色光波分别发自光 源S,和S,P点是两光波相遇区域内的任 意一点,P到S,和S的距离分别为,和 「,因此,两光波各自在P点产生的光振动 s1- 可以写为 B=aw2(停-头)2-D 52 E=0,co2(信-头)(2-2) 图2-1两光波在P点达加 式中,和a:分别为两光波的振幅。根据迭加原理,在P点的合振动为 B=B+E,=a,co2(片-天a,co2(存-头) 令4,=-2”,4,=-2,上式化为

31 E=acos(ot+a)+a,cos(o!+a;) 应用两角和的余弦公式,此式可展开为 E=a,cosotcosa,-a sinoisina +acosofcosa-asinclsinaa =(a cosa +a,cosa,)cosot -(a,sina,+a:sina:)sint 因为a,a,和a,a:都是常数,所以可令 a,cosa,+a,cosa,=Acos a (2-3) +asina,=Asin a (-4) 两式中A和α均为待定常数。把两式平方后相加,得到 A (sin'a+eosa)=a(sin a,+cosa) +a(sina:+cos2a) 2a,a,(cosa cosa,sina sina,) =a+a+2a,a,cos(a,-a2) (2-5) 将式(2-3)除式(2-4)得到 a sina,a,sing, tan a (2-6) a cosa +a.cos 因此,P点的合振动可写为 E=Acos a cosot-Asin a sinwot Acos(ot+a) (2-7) 可见,P点的合振动也是一个简谐振动,振动频率和振动方向都与两单色光波相同,振幅A 和初位相a分别由式(2-5)和(2-6)决定。 如果所讨论的两单色光波的振幅相等,即=a,=a,则P点的合幅由下式决定 A=a+a 2aacos(a-g) =n+2a2cos6-48o3号 或以光强度表示 1=4l,cos29 (2-8) 式中。=,是单个光被的强度。上式表在P点的迭加光强度决定于位相差。=(a: α,)。当位相差为的侧数倍时,即 8三+2mn(m=0.1.2.+.) (2-9) 时,【=4。,P点光强度达到最大值。而当位相差为π的奇数倍时,即 8=士(2m+】》算 (2-10) 时,【=0,P点的光强度有最小值。位相差介于两者之间时,P点强度在0和41,之闻。 因此,很明显,如果两光波在光源处的位相相同,那么两光波在P点的位湘差是由于从两光 源到P点的距离不同而引起的。我们很容易把位相差表示为P点到两光源的距离,和:之 差。因为a,=- ,a=-2ur; 2元r, ,所以

2 6=a,-a,-21-rd 式中入为光波在介质中的波长,入= 行,。为真空中的波长,n为介质的折射率。这样上 式又可写为 通常为简便起见,把λ。仍写作入,表示真空中波长,因而 6=2要a,-r) (2-11) 式中n(r:~r)是光程差,以后用符号A表示。光程差是从光源S,和S:到P点的光程之 差。所谓光程,就是光波在某一种介质中所通过的几何路程和这介质的折射率的乘积。采 用光程概念的好处是,可以把光在不同介质中的传播路程都折算为在真空中的传播路程,便 于相互进行比较。式(2-11)在物理光学中是 个重要的关系式,表示从两个不同的光源到考 察点P的光程差和它所引起的位相差之间的关系。根据这个关系式,也可以把在P点产生最 大光强度的条件〔式(2-9)门写为 △=n(-r)=土mA(m=0,1,2,…) (2-12 即光程差等于波长的整数倍,把在P点产生最小光强度的条件〔式(2-10)写为 △=n(-r)=土(2m+1)2(m=0,1,2…) (2-13) 即光程差等干半波长的奇数倍。 应该指出:写出式(2-1)和(2-2)时,实际上是假设在S,和S:两点光振动的初位相 (1=0时的位相)为零。如果在S,和S:两点的初位相不同,则式(2-11)所表示的两光 波在P点的位相差还必须加上S,和S,的初位相差这一项。 显而易见,在两光被迭加区域内,不同的点将有不同的光程差,因而就有不同的光强 度。满足条件(2-12)的点,光强度最大满足条件(2-13)的点,光强度最小,其余的点 介于最大强度和最小强度之间。只要两光波的初位相差保持不变(现在讨论的理想单色光波 便是这样),在选加区域内各点的强度分布也是不变的。我们把这种在迭加区域出现的光强度 稳定的强弱分布的现象称为光的干涉,把产生光干涉的光波称为相干光波,而把光源称为相 千光源。 但是我们知道,实际光源发出的光波并不是理想的单色光波, 它是由一段段有限长的被 列组成的。由于每一段波列的初位相和偏振方向是无规则变化的,所以实际光波产生干涉必 须满足一些条件,这些条件我们将在第三章里加以详细讨论。 求解两个或多个光波的选加问题,常常还应用另外两种较为简便的方法,现分别介绍如 下。 一、复数方法 采压女数表式时,光源S,和S,发出的单色光波在P点产生的光振动可以写为 E,=a1e-1©1+d (2-140 E1=0e-() (2-15)