
合振动为 E=B,+E,=a,e-i)+a4e+) =(a,e-i1+a,e-i)e-i® (2-16) 上式括号内两复数之和仍为一复数,设 Ae-10=0,e-l"1+a,e-g (2-170 并代入式(2-16),得到 E=Ae-le.e-ist=Ae-i(n) (2-18) 这一结果与式(2-?)相对应。P点的合振动的振幅4容易由复数运算求得 A=(4e-9)(Ae-i) =(a,e-i1+a8-i)(a,e-i"1+0e-“) =a+a号+a1a,0e1-“1+e-t-门 a+aj+2a,d;cos(a,-a:? (2-19) 为求到合振动的初位相α,把式(2-17)右边的复数式展开为三角函数式 e=a,cosa,+a,cosa,-i (a,sina,+asina,) 根据复数的性质,得到 (2-20) 式(2-19)和(2-20)与式(2-5)和(2-6)完全相同。 二、振辐矢加法 这是一种图解法,这种方法利用振幅矢量的概念:损帽矢量·,它的长度代表某一振动 的振幅大小,它与某一给定轴—一ox轴的夹角相当于该振动的位相。图2-2画出了初始:时 刻的振幅矢量a,和a,的位置若两矢量绕。点以角 速度0反时针方向旋转,则两矢量的末端在。x轴上 投形的运动便表示两个简谐振动 E,=a cos(+a) E.a.cos(ot+a.) 随若a,和a绕0点以角速度o反时针方向旋转,显 然a,和a,的合矢量A(利用平行四边形加法求出)也 图2-2振幅矢城相加 绕。点以同一角速度反时针方向旋转,且A的未端在 0x轴上投影的运动也为一简谐振动 E=Acos(ot+a) 式中a是振动的初位相。显然,A在ox轴上投影的 运动等于a和4,在ox轴上投影的运动之和,即E =E,+E,。因此两个单色光波在某一点的光振动的 送加可以通过它们的振幅矢量相加而求得。由图2-2 可见 =+a+2a,a;cos(a,-a) 和 tana=,siag a,cosa,+a.c 图2-3五个振幅矢盘相加

它们分别为合振动的振幅和初位相,结果与式(2-5)和(26)完全一致。 振幅矢量加法对于求多个谐振动的合成特别有用。这时可应用矢量的多边形加法求出 矢量a、a、a,…a.等的合矢量A。如果不是要求很精确时,可根据合矢景的长度和与 ·x轴的夹角估计合振动的振幅和位相的大小。图2-3表示五个振幅失量的多边形加法,两 相邻矢量间的夹角为两相应振动的位相差。 §2-2驻波 两个频率相同,振动方向相同而传播方向相反的单色光波,例如垂直入射到两种介质分 界面的单色光波与反射波的选加,产生驻波。 假定光波反射面是:=0平面,之的正方向指向入射波所在的介质,其折射率为,另 一介质的折射率为m:(图2-4),如果正入射的单色光波的波动公式为 图2-4驻波 E,=acos (t+k) 则在z=0平面反射的光波的波动公式为 E=a cos(ot-ka+) 式中。表示反射时的位相变化,反射波的振幅与入射波相同是我们假设两种介质分界面的反 射率很高。当>n:时,8=,当n:<,时,8=0.2符号的改变,相当于传播方向 相反。反射波与入射波的迭加,得到 E=E+E;=acos(ot+kz)+acos(of-kz+8) 将余弦函数展开并化简 E=2acos)cos1+3) (2-21) 因子2a(:-)与时间无关,表示合成波的振幅4,更确切些说,振(是一个正量)等 于这个因子的绝对值 A-2aco(-》 (2-22) 可见振瓶随2值而变,表明对于介质中不同的点有不同的振幅,这种波称为驻波。在驻波中 有一系列振幅为零的点,这些点称为波节,有另外一些点,振幅等于两送加光波的振幅之和
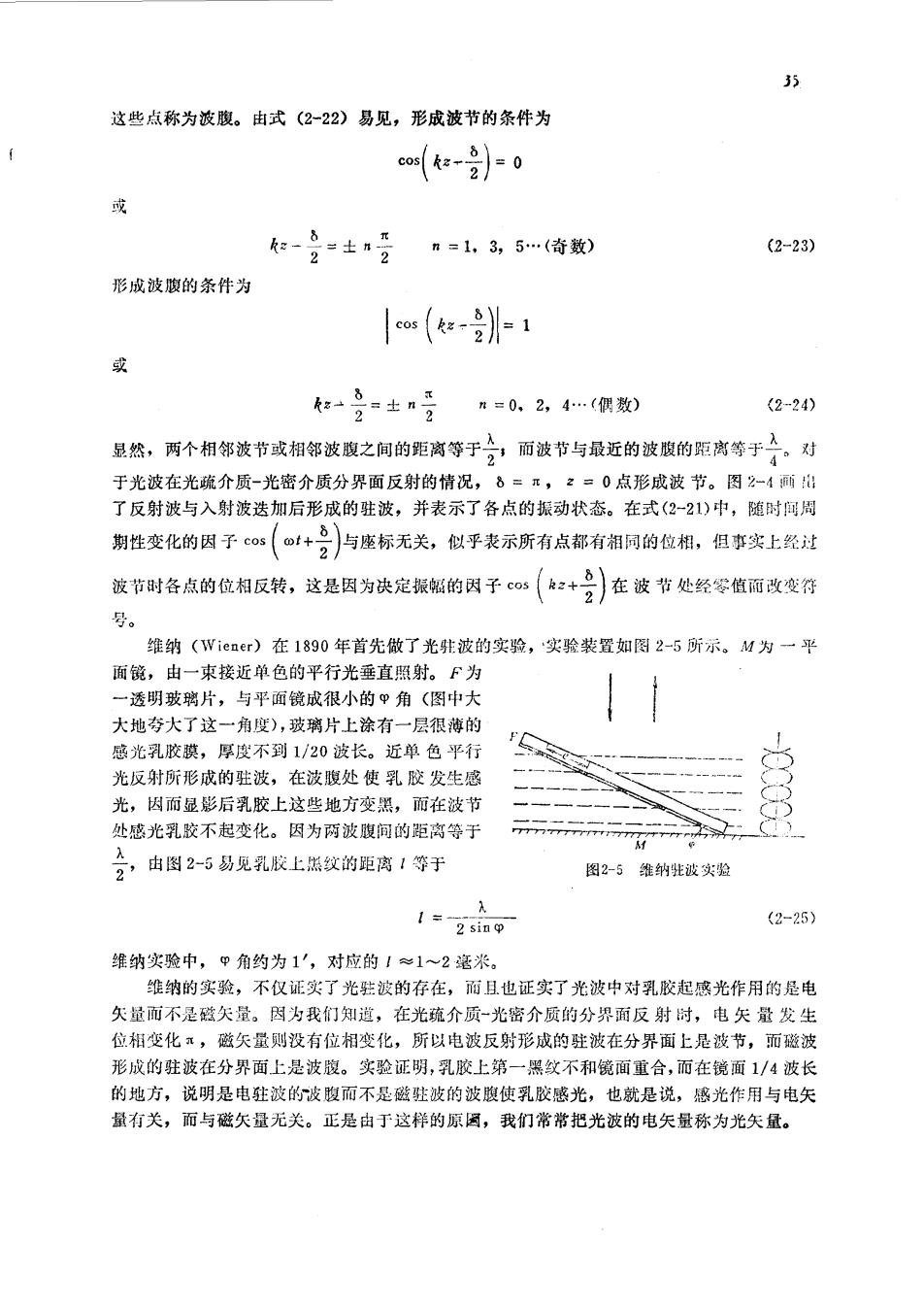
这些点称为波腹。由式(2-22)易见,形成波节的条件为 co(e-2)=0 或 e-8=士 n-1,3,5…(奇数) (2-23) 形成波腹的条件为 cos (k-2)1 或 小分=士n =02,4…(偶数) 2-240 显然,两个相邻波节或相邻波腹之间的距离等于而波节与最近的波腹的距离等于。对 于光波在光疏介质-光密介质分界面反射的情况,8=,:=0点形成波节。因2-4面指 了反射波与入射波迭加后形成的驻波,并表示了各点的振动状态。在式(221)中,随时闻周 期性变化的因子o(©+合)与座标无关,似平表示所有点都有相同的位相,但事实上经过 行时备点的位相反转,这是因为决定议的因子心(:+》在波节处经零值面改变特 号。 维纳(Wiener)在1890年首先做了光驻波的实验,实验装置如图2-5所示。M为一平 面镜,由一束接近单色的平行光垂直照射。F为 一透明玻瑞片,与平面镜成很小的甲角(图中大 大地查大了这一角度),玻璃片上涂有一层很道的 感光乳胶膜,厚度不到1/20波长。近单色平 光反射所形成的驻波,在波腹处使乳胶发生感 光,因而显影后乳胶上这些地方变照,而在波节 处感光乳胶不起变化。因为两波腹间的距离等于 合,由图2-5易见乳胶上然纹的距离1等于 图2-5雏纳驻波实验 1=209 (2-25) 维纳实验中,甲角约为1',对应的1≈1~2毫米。 维纳的实验,不仅证实了光驻波的存在,而且也证实了光波中对乳胶起感光作用的是电 矢量而不是登矢量。因为我们知,在光硫介质~光密介质的分界面反射时,电矢量发生 位相变化,磁矢量则没有位相变化,所以电波反射形成的驻波在分界面上是波节,而磁波 形成的驻波在分界面上是波腹。实验证明,乳胶上第一黑纹不和镜面重合,而在镜面1/4波长 的地方,说明是电驻波的波腹而不是磁驻波的波腹使乳胶感光,也就是说,感光作用与电矢 量有关,而与磁矢量无关。正是由于这样的原固,我们常常把光波的电矢量称为光矢量

光驻波是李普曼(Lippmanr)彩色照相法的基础(1891年),它使用的照相底片有一 层很厚的感光乳胶,且乳胶面背向入射光,与水银镜面相接触(图26)。垂直射入的光经 水银镜面反射在乳胶层内形成驻波,对应于波腹所在的 地方,乳胶产生感光作用,所以显影后形成一系列与底 底片 片表面平行的银层。若乳胶某处入射光波长为λ,则对应 该处的丙银层间距离等于。以后观看这底片时,入 白光 射光为白光(包含可见光各种波长),各种波长相继由 上述一系列银层反射,但唯有波长入,的光波在该处反 射最为强烈,因为由相邻银层反射的光波的光程差 为,光波干涉的结果将互相加强,而对其它波长的光 并不满足干涉加强条件,所以从底片该处反射的光呈 现出原来感光时的颜色。 图2-6李普曼彩色照相法原理 §2-3两个频率相同、振动方向互相垂直的光波的迭加 如图2-?所示,假设光源S,和S:发出两个频率相同而振动方向互相垂直的单色光波, 一个波的振动方向平行于x轴,另 一个波的振动方向平行于y轴。现 在考察它们沿:轴方向传播时的迭 加。取:轴上任一点P,显然两单 色光波在该点产生的光振动可写 为 图2-7两个频率相同,振动方向互相垂直的光被的选加 ,=4w(ot-2g) E,=a(t-2受) 式中:,和分别为两光源到P点的距离,且为简单起见,假设在S,和S,光振动的初位相 为零。令a,= 2x2 2x2 2,因而上面两式化为 E.=a,cos(of +a.) (2-26) E,=agcos(ot+a:) (2-27) 由于E,和E,分别在×方向和y方向,所以这两个光振动的迭加必需按迭加原理作矢量相 加。易见,合矢量的大小和方向都是随时间变化的,合矢量末端的运动轨迹可由上面两式中 消去而得到,为此将上面两式写戒 (2-28) Bcotco (2-29) 以cosa,乘式(2-28),以cosa,乘式(2-29),然后把两式相诚,得到

37 E.cos (2-30 以sina,乘式(2-28),以sina,乘式(2-29),再将两式相减,得到 (2-31) 将式(2-30)和(2-31)平方后相加便可以消去:,最后得出合矢量末端的轨迹方程式 (2-32) a,02 一般说来,这方程式是椭圆方程式,表示合矢量末端的轨迹为一椭圆。这椭圆内接于一长方 形,长方形各边与座标轴平行,边长为2a,和2@:(图2-8)。可以证明,椭圆的长轴和x轴 的夹角中由下式决定 2a,a tan2t=aa:cosǒ (2-33) 式中。=a:-a,是振动方向平行于y轴的光波与振动方向平行于x轴的光波的位相鉴。我 们把电矢量末端的运动描成一椭圆的这种光称为椭圆偏振光。因此,使两个频率相同,振动 方向互相垂直且具有一定位相差的光波迭加,一般可以得到椭圆偏振光。 ☑☑N 2 <6< d= d<2 h) 图2-8偏板椭圆 图2-9位相差取不同值时的椭时偏指 图2-9是根据式(2-32)画出的与几种不同8值对应的偏振椭圆的形状,可见椭倒的形 状由两迭加光波的位相差8和振幅比©/©1决定。在两种特殊的情况下,合成电矢量的运动 沿直线进行,因而合成光波仍为线偏振光。这两种特殊的情况是: (一)8=0或士2m的整数倍,这时式(2-32)化为 E,=82E, (2-34) 表示合成电矢量的运动沿着一条经过座标原点而斜率为a,/a,的直线进行,如图2-9所。 (二)8=士的奇数倍,这时式(2-32)化为 E,=-8E (2-35) 表示合成电矢量的运动沿者一条经过座标原点而斜率为-a:/©,的直线进行,如图2-9c所尔。 还可以指出,当。=士2和它们的奇数倍时,式(2-2)化为 +1 (2-36)