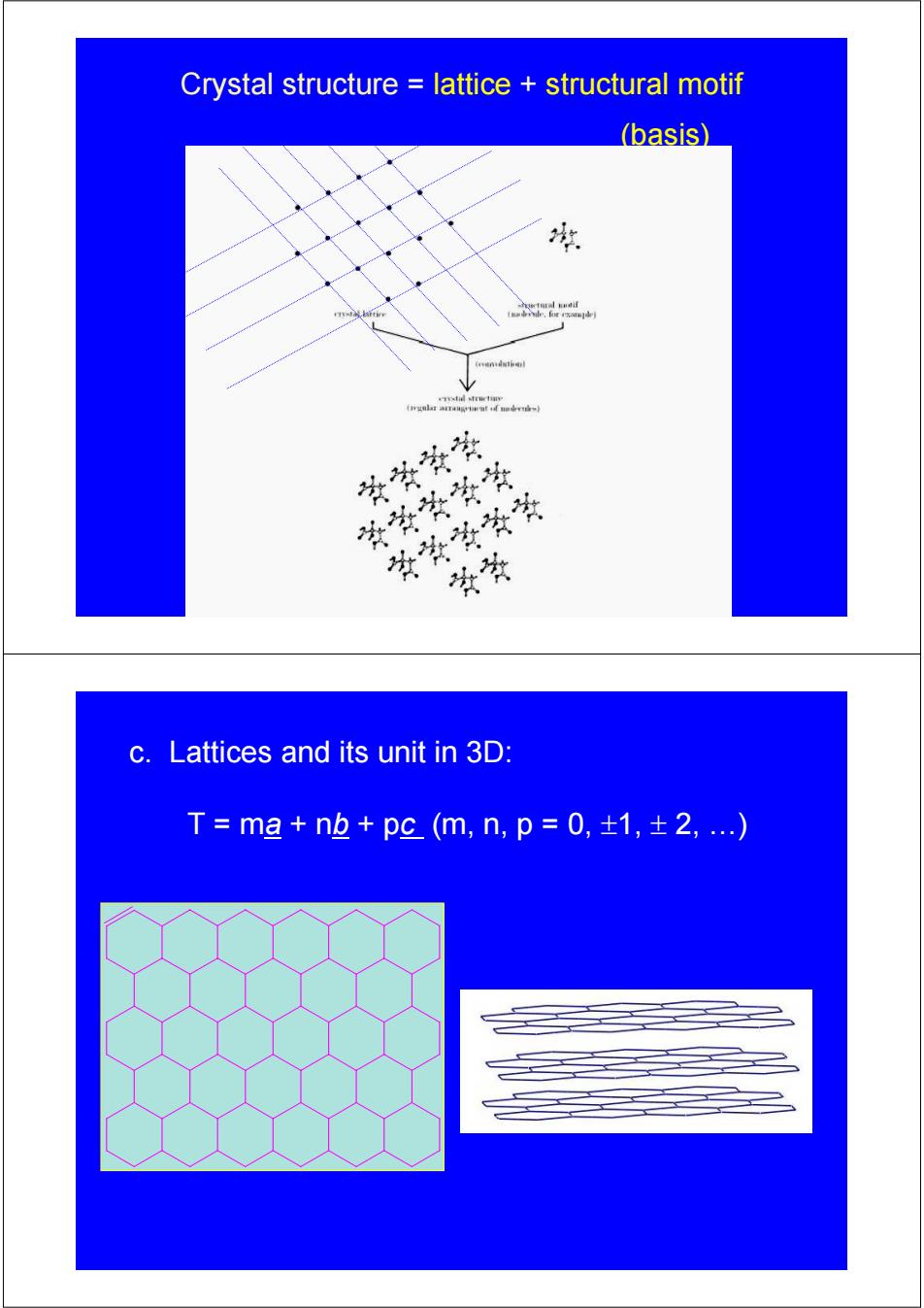
Crystal structure lattice structural motif (basis) 球 14 黄学资学 学学冬学学 草安学学常 头爷 c.Lattices and its unit in 3D: T=mg+n也+pc(m,n,p=0,±1,±2,)
Crystal structure = lattice + structural motif (basis) c. Lattices and its unit in 3D: T = ma + nb + pc (m, n, p = 0, ±1, ± 2, …)

The Choice of a Unit Cell:Have maximum symmetry and minimum size B a b a The Choice of a Primitive Cell B/a 1)The axial system should be right handed b 2)The basis vectors should coincide as much as possible with directions of highest symmetry 3)Should be the smallest volume that satisfies condition 2 4)Of all lattice vectors none is shorter than a 5)Of those not directed along a none is shorter than b 6)Of those not lying in the a,b plane none is shorter than c 7)The three angles between the basis vectors a,b,c are either all acute or obtuse
a b c α β γ The Choice of a Unit Cell: Have maximum symmetry and minimum size a b c 1) The axial system should be right handed 2) The basis vectors should coincide as much as possible with directions of highest symmetry 3) Should be the smallest volume that satisfies condition 2 4) Of all lattice vectors none is shorter than a 5) Of those not directed along a none is shorter than b 6) Of those not lying in the a, b plane none is shorter than c 7) The three angles between the basis vectors a,b,c are either all acute or obtuse The Choice of a Primitive Cell

Atomic Coordinates:Fractional coordinates Fractional coordinates: The positions of atoms inside a unit cell are specified using 0.5 fractional coordinates(x,y,z). These coordinates specify the position as fractions of the unit 0.6 6 cell edge lengths i:(1.0,0.6,0.5 Example: Cubic unit cell of CsCl, The Crystal Structure a=b=c =β=Y=90° Cs:(0,0,0) C:(112,112,112) Single Crystal:Composed of only one particular type of space lattice Polycrystalline matter:Clusters of multiple crystals
Atomic Coordinates: Fractional coordinates 0.5 0.6 i i: (1.0, 0.6, 0.5) Fractional coordinates: The positions of atoms inside a unit cell are specified using fractional coordinates(x,y,z). These coordinates specify the position as fractions of the unit cell edge lengths Example: Cubic unit cell of CsCl, a=b=c α=β=γ=90° Cs:(0,0,0) Cl: (1/2,1/2,1/2) Single Crystal: Composed of only one particular type of space lattice. Polycrystalline matter: Clusters of multiple crystals
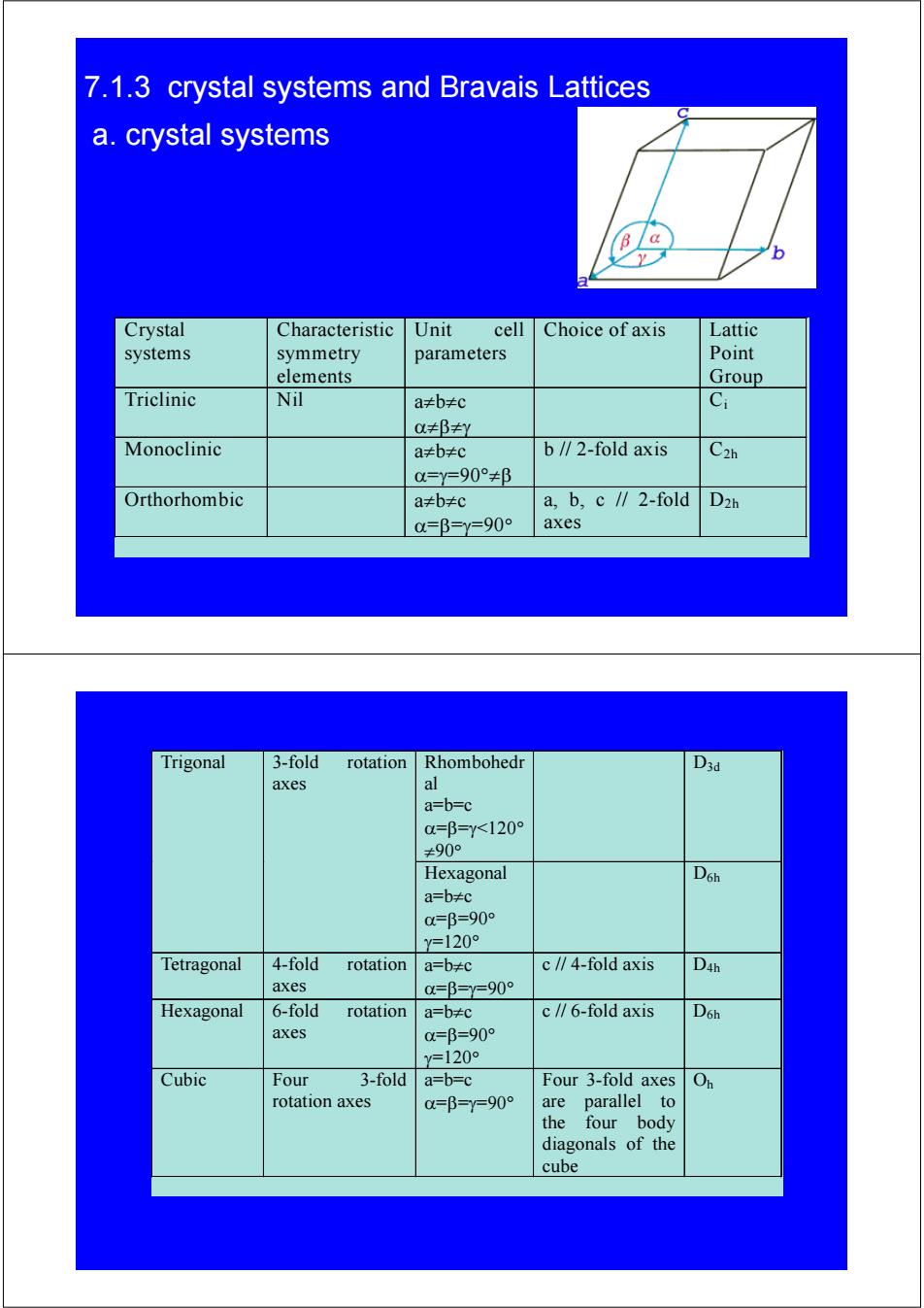
7.1.3 crystal systems and Bravais Lattices a.crystal systems B/a b Crystal Characteristic Unit cell Choice of axis Lattic systems symmetry parameters Point elements Group Triclinic Nil a≠b≠c Ci 0≠βy Monoclinic a≠b≠c b∥2-fold axis C2h 0=Y=90°≠β Orthorhombic a≠b≠c a,b,c∥2-fold D2h 0=β=y=90° axes Trigonal 3-fold rotation Rhombohedr D3d axes a=b=c 0=β=y<120° ≠90° Hexagonal D6h a=b≠c 0=β=900 Y=120° Tetragonal 4-fold rotation a=b≠c c/∥4-fold axis D4h axes 0=β=Y=90° Hexagonal 6-fold rotation a=b≠c c∥6-fold axis D6h axes 0=β=90° y=120 Cubic Four 3-fold a=b=c Four 3-fold axes On rotation axes a=β=y=90° are parallel to the four body diagonals of the cube
a. crystal systems Crystal systems Characteristic symmetry elements Unit cell parameters Choice of axis Lattic Point Group Triclinic Nil a≠b≠c α≠β≠γ Ci Monoclinic a≠b≠c α=γ=90°≠β b // 2-fold axis C2h Orthorhombic a≠b≠c α=β=γ=90° a, b, c // 2-fold axes D2h 7.1.3 crystal systems and Bravais Lattices Rhombohedr al a=b=c α=β=γ<120° ≠90° Trigonal 3-fold rotation D3d axes Hexagonal a=b≠c α=β=90° γ=120° D6h Tetragonal 4-fold rotation axes a=b≠c α=β=γ=90° c // 4-fold axis D4h Hexagonal 6-fold rotation axes a=b≠c α=β=90° γ=120° c // 6-fold axis D6h Cubic Four 3-fold rotation axes a=b=c α=β=γ=90° Four 3-fold axes are parallel to the four body diagonals of the cube Oh
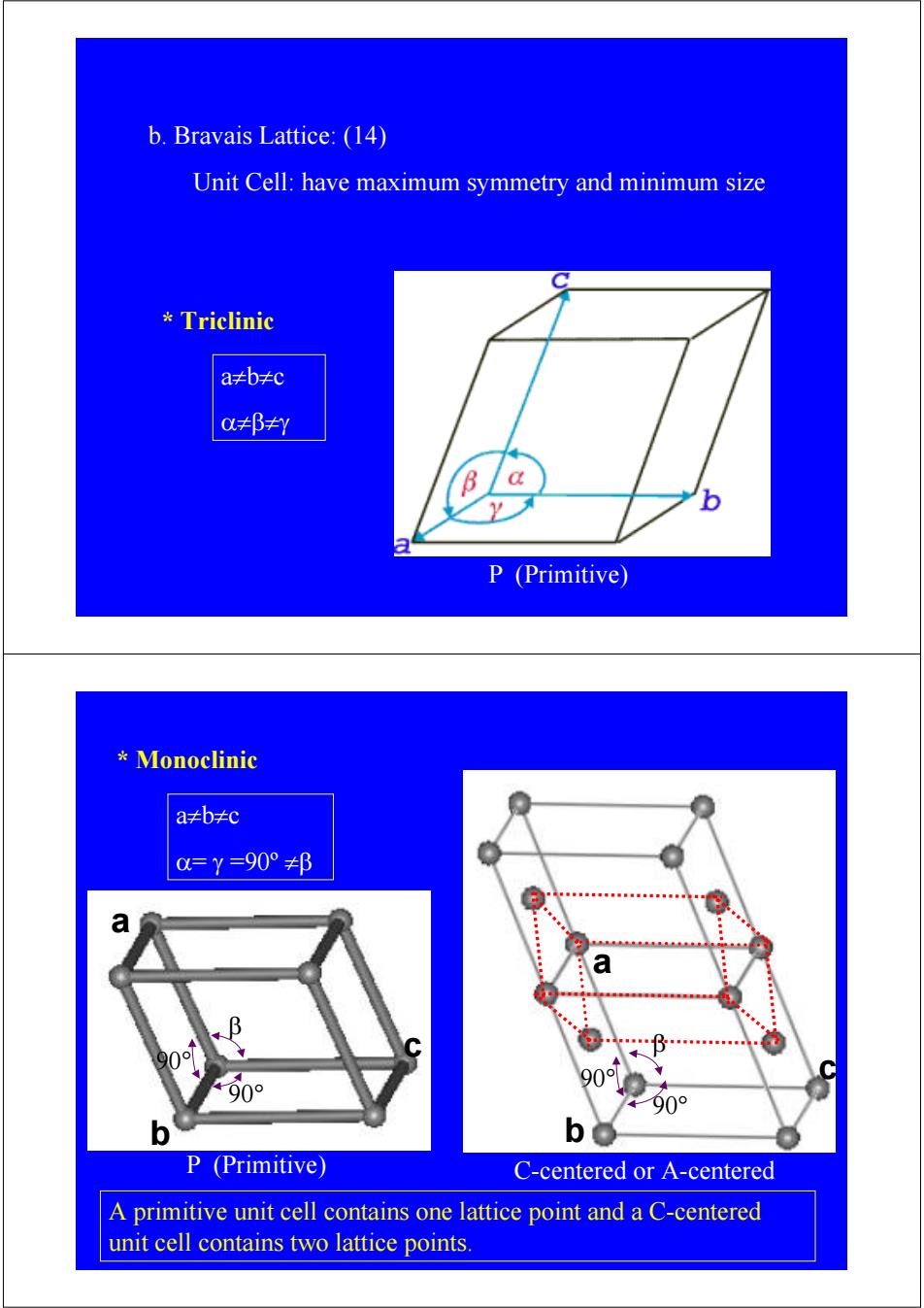
b.Bravais Lattice:(14) Unit Cell:have maximum symmetry and minimum size Triclinic a≠b≠c oa≠βy P (Primitive) Monoclinic a≠b≠c 0=Y=90°≠β 8 a a 0 0 90o 90° b P (Primitive) C-centered or A-centered A primitive unit cell contains one lattice point and a C-centered unit cell contains two lattice points
b. Bravais Lattice: (14) Unit Cell: have maximum symmetry and minimum size * Triclinic a≠b≠c α≠β≠γ P (Primitive) b a c 90° 90° β * Monoclinic a≠b≠c α= γ =90º ≠β P (Primitive) b 90° 90° β a c C-centered or A-centered A primitive unit cell contains one lattice point and a C-centered unit cell contains two lattice points