
Chapter 3 Molecular symmetry and symmetry point group 1 Symmetry elements and symmetry operations >Symmetry exists all around us and many people see it as being a thing of beauty. >A symmetrical object contains within itself some parts which are equivalent to one another. >The systematic discussion of symmetry is called Some objects are more symmetrical than others
Chapter 3 Molecular symmetry and symmetry point group §1 Symmetry elements and symmetry operations ¾Symmetry exists all around us and many people see it as being a thing of beauty. ¾A symmetrical object contains within itself some parts which are equivalent to one another. ¾The systematic discussion of symmetry is called : Some objects are more symmetrical than others

Why do we study the symmetry concept? >The molecular configuration can be expressed more simply and distinctly. >The determination of molecular configuration is greatly simplified. >It assists giving a better understanding of the properties of molecules. >To direct chemical syntheses;the compatibility in symmetry is a factor to be considered in the formation and reconstruction of chemical bonds. 1.Symmetry elements and symmetry operations symmetry operation .A action that leaves an object the same after it has been carried out is called symmetry operation. Example: Any rotation of sphere around axis through center brings sphere over into itself
¾ The molecular configuration can be expressed more simply and distinctly. ¾The determination of molecular configuration is greatly simplified. ¾It assists giving a better understanding of the properties of molecules. ¾To direct chemical syntheses; the compatibility in symmetry is a factor to be considered in the formation and reconstruction of chemical bonds. Why do we study the symmetry concept? symmetry operation •A action that leaves an object the same after it has been carried out is called symmetry operation. Any rotation of sphere around axis through center brings sphere over into itself Example: 1. Symmetry elements and symmetry operations
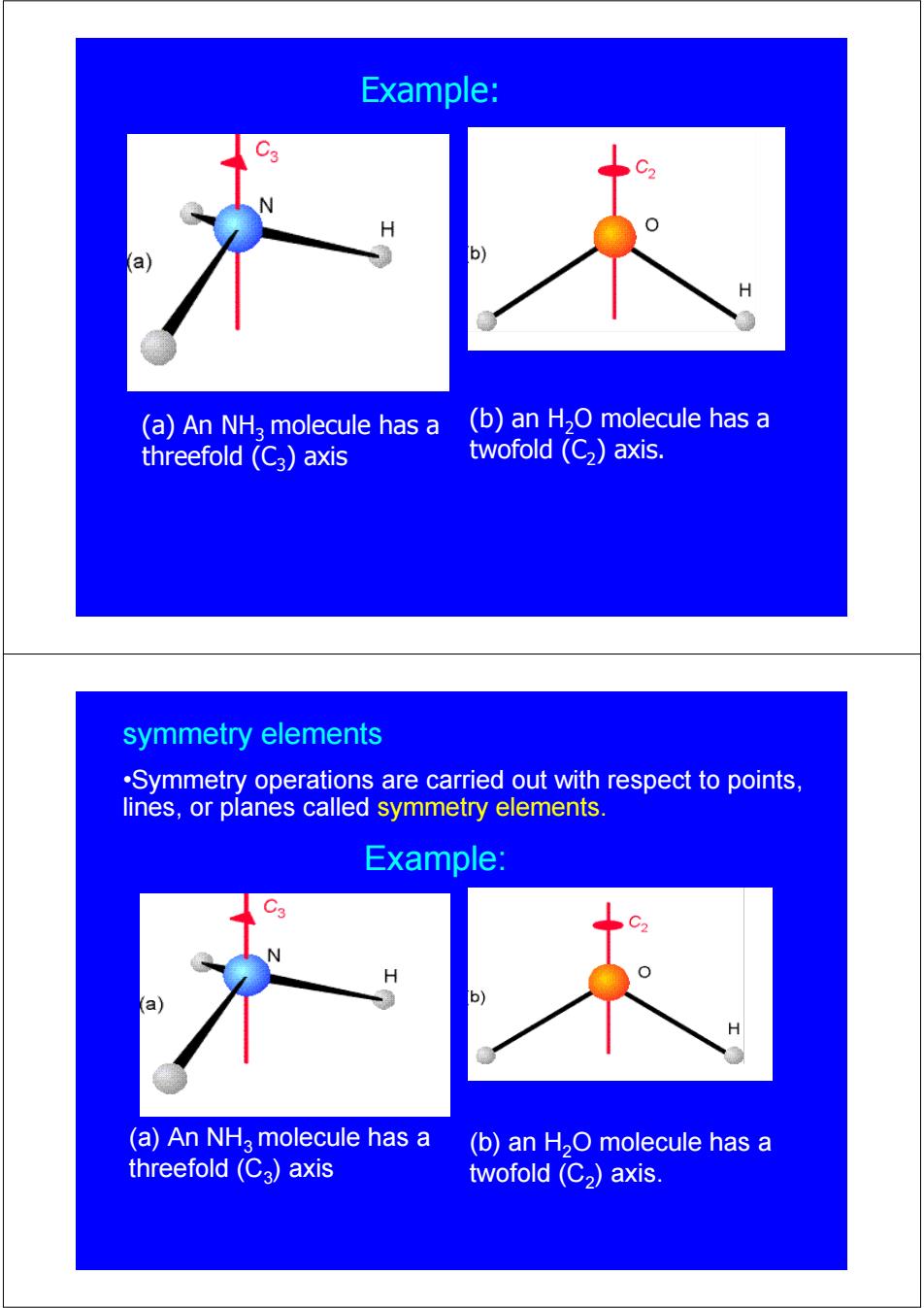
Example: (a)An NH2 molecule has a (b)an H2O molecule has a threefold (C3)axis twofold (C)axis. symmetry elements .Symmetry operations are carried out with respect to points, lines,or planes called symmetry elements. Example: (a)An NHa molecule has a (b)an H2O molecule has a threefold(Ca)axis twofold (C2)axis
(b) an H2O molecule has a twofold (C2) axis. (a) An NH3 molecule has a threefold (C3) axis Example: (b) an H2O molecule has a twofold (C2) axis. (a) An NH3 molecule has a threefold (C3) axis Example: •Symmetry operations are carried out with respect to points, lines, or planes called symmetry elements. symmetry elements

Symmetry elements 03 Some of the symmetry elements of a cube, the twofold,threefold,and fourfold axes. Symmetry Operation Symmetry operations are: Rotation Reflection nversion 60I UOI2LSAUI The corresponding symmetry elements are: aa如e a point
Some of the symmetry elements of a cube, the twofold, threefold, and fourfold axes. Symmetry elements Symmetry operations are: The corresponding symmetry elements are:
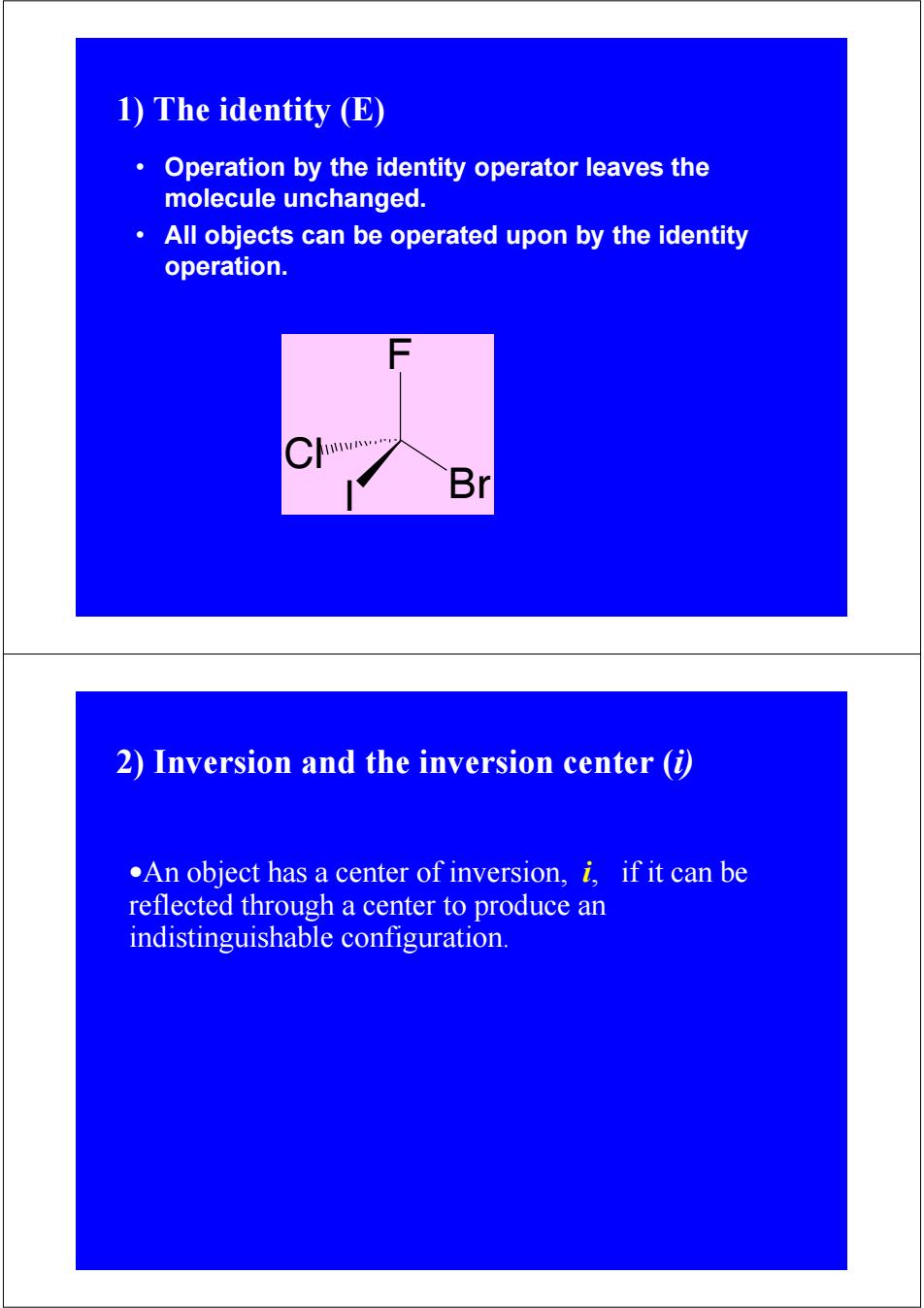
1)The identity (E) Operation by the identity operator leaves the molecule unchanged. All objects can be operated upon by the identity operation. Br 2)Inversion and the inversion center (i) .An object has a center of inversion,i,if it can be reflected through a center to produce an indistinguishable configuration
I F Cl Br • Operation by the identity operator leaves the molecule unchanged. • All objects can be operated upon by the identity operation. 1) The identity (E) 2) Inversion and the inversion center (i) •An object has a center of inversion, i, if it can be reflected through a center to produce an indistinguishable configuration