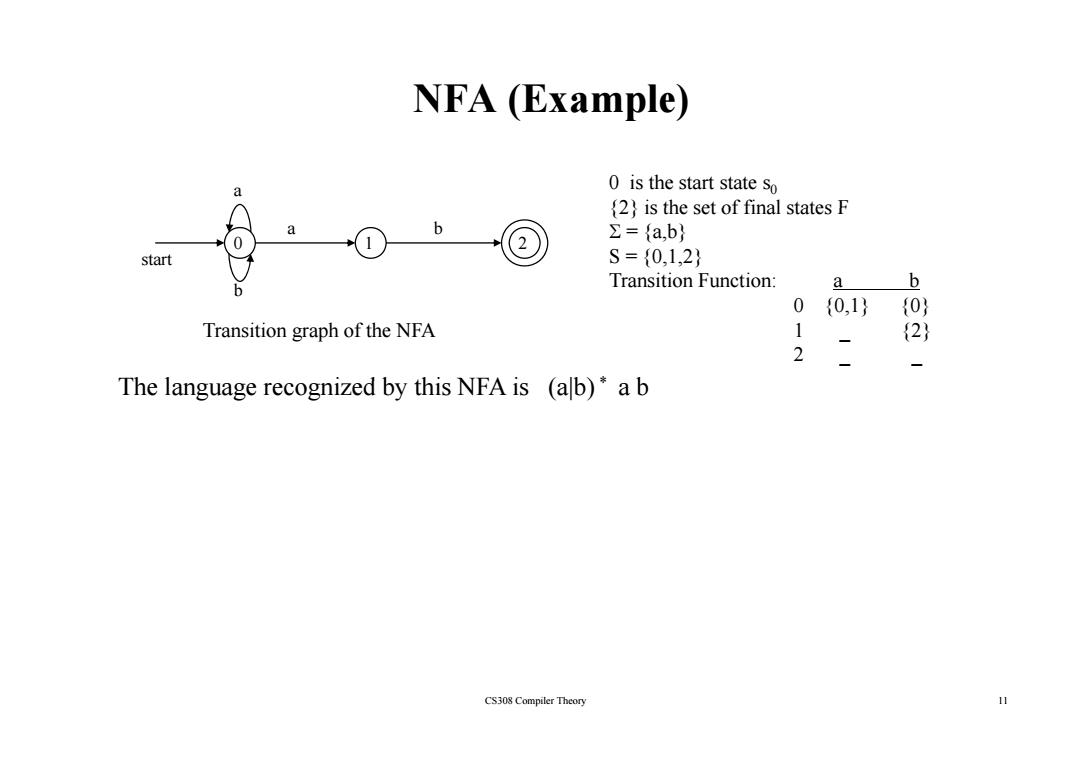
NFA (Example) a 0 is the start state so (2)is the set of final states F b ∑={a,b} start S={0,1,2} Transition Function: Q b 0{0,1} {0} Transition graph of the NFA 1 {2} 2 The language recognized by this NFA is (alb)*a b CS308 Compiler Theory 11
NFA (Example) a 0 is the start state s0 {2} is the set of final states F 0 2 1 a b start b {2} is the set of final states F Σ = {a,b} S = {0,1,2} Transition Function: a b b 0 {0,1} {0} 1 _ {2} 2 _ _ Transition graph of the NFA Th l i d b thi NFA i ( |b) * The language recognized by this NFA is (a|b) b * a CS308 Compiler Theory 11

Deterministic Finite Automaton (DFA) A Deterministic Finite Automaton (DFA)is a special form of a NFA. no state has s-transition for each symbol a and state s,there is at most one labeled edge a leaving s. i.e.transition function is from pair of state-symbol to state(not set of states) a The language recognized by this DFA is also (ab)*a b b CS308 Compiler Theory 12
Deterministic Finite Automaton (DFA) • A Deterministic Finite Automaton (DFA) is a special form of a NFA A Deterministic Finite Automaton (DFA) is a special form of a NFA. • no state has ε- transition • for each symbol a and state s, there is at most one labeled edge a leaving s. i t iti f ti i f i f t t i.e. transition function is from pair o f s t a te-symb lt t t ( t t f t t ) b o l to s t a te (no t se t o f s t a tes ) a b a The language recognized by b a 0 2 1 a b b this DFA is also (a|b) * a b CS308 Compiler Theory 12

Conversion of an NFa to a dFa initially,e-closure(so)is the only state in Dstates,and it is unmarked; while there is an unmarked state T in Dstates ) mark T; for each input symbol a ) U=e-closure(move(T,a)); if (U is not.in Dstates) add U as an unmarked state to Dstates; DtranT,a]=U; CS308 Compiler Theory
Conversion of an NFA to a DFA CS308 Compiler Theory 13

Converting A Regular Expression into A NFA (Thomson's Construction) This is one way to convert a regular expression into a NFA. There can be other ways(much efficient)for the conversion. Thomson's Construction is simple and systematic method. It guarantees that the resulting NFA will have exactly one final state, and one start state. Construction starts from simplest parts(alphabet symbols). To create a NFA for a complex regular expression,NFAs of its sub-expressions are combined to create its NFA, CS308 Compiler Theory 14
Converting A Regular Expression into A NFA (Thomson’s Construction) (Thomson’s Construction) • This is one way to convert a regular expression into a NFA. • There can be other ways (much efficient) for the conversion. • Thomson’s Construction is simple and systematic method. It guarantees that the resulting NFA will have exactly one final state, and one start state. • C t ti t t f i l t t ( l h b t b l ) Cons truction s tar ts from s imp les t par ts ( a l p h a b e t sym b o l s ). To create a NFA for a complex regular expression, NFAs of its sub -expressions are combined to create its NFA expressions are combined to create its NFA, CS308 Compiler Theory 14
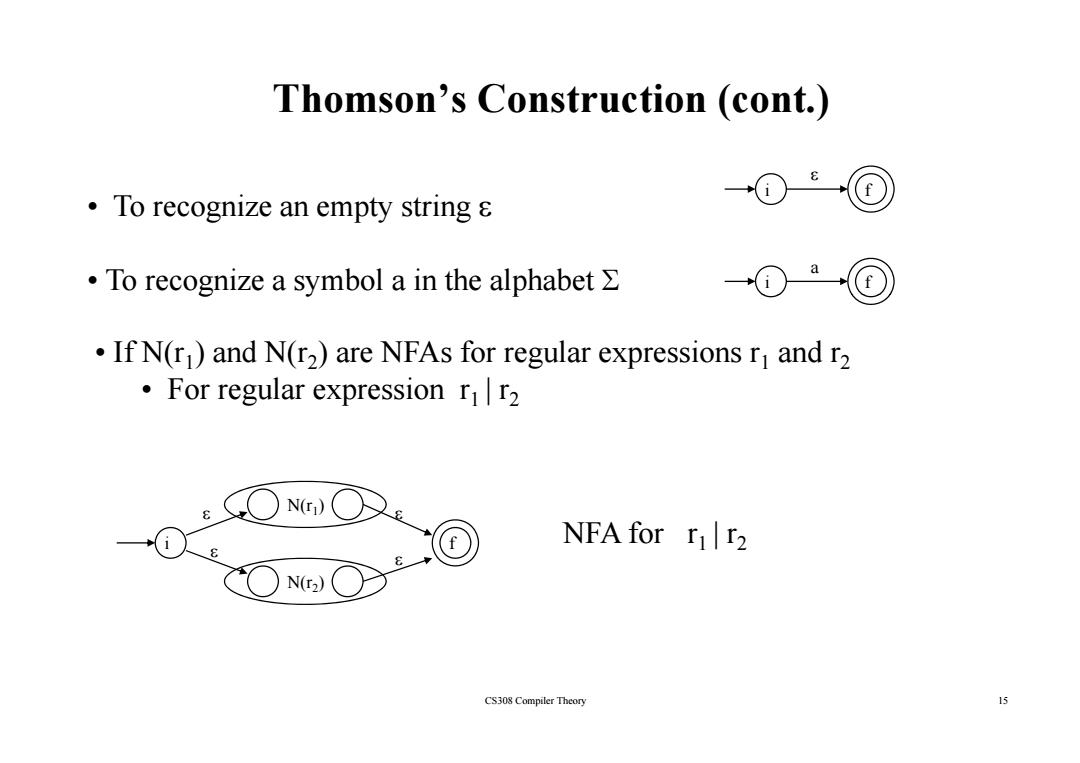
Thomson's Construction (cont.) ① To recognize an empty string 8 ·To recognize a symbol a in the alphabet∑ If N(r)and N(r2)are NFAs for regular expressions ri and r2 For regular expression rr2 N() NFA for r r2 N(I2) CS308 Compiler Theory 15
Thomson’s Construction (cont.) • To recognize an empty string ε i f ε • To recognize an empty string ε • To reco gnize a s ymbol a in the al phabet Σ a gy p i f • If N(r1) and N(r 2) are NFAs for regular expressions r1 and r 2 • Fl i or regu lar express ion r | 1 r 2 N(r1) i f NFA for r1 | r 2 ε ε ε N(r2) ε CS308 Compiler Theory 15