
Syntax Analyzer CS308 Compiler Theory
Syntax Analyzer CS308 Compiler Theory 1

Syntax Analyzer Syntax Analyzer creates the syntactic structure of the given source program. This syntactic structure is mostly a parse tree. Syntax Analyzer is also known as parser. The syntax of a programming is described by a context-free grammar (CFG).We will use BNF(Backus-Naur Form)notation in the description of CFGs. 。 The syntax analyzer(parser)checks whether a given source program satisfies the rules implied by a context-free grammar or not. -If it satisfies,the parser creates the parse tree of that program. Otherwise the parser gives the error messages. A context-free grammar gives a precise syntactic specification of a programming language. -the design of the grammar is an initial phase of the design of a compiler. a grammar can be directly converted into a parser by some tools. CS308 Compiler Theory 2
Syntax Analyzer • Syntax Analyzer creates the syntactic structure of the given source program. • Thi i i l This syntactic structure is mostly a parse tree. • Syntax Analyzer is also known as parser. • The syntax of a programming is described by a The syntax of a programming is described by a context context-free grammar (CFG) free grammar (CFG). We will We will use BNF (Backus-Naur Form) notation in the description of CFGs. • The syntax analyzer (parser) checks whether a given source program satisfies the rules i li d b implied by a context-free grammar or not. – If it satisfies, the parser creates the parse tree of that program. – Otherwise the parser gives the error messages. • A context-free grammar – gives a precise syntactic specification of a programming language. – the desigg p g p n of the grammar is an initial phase of the design of a compiler. – a grammar can be directly converted into a parser by some tools. CS308 Compiler Theory 2
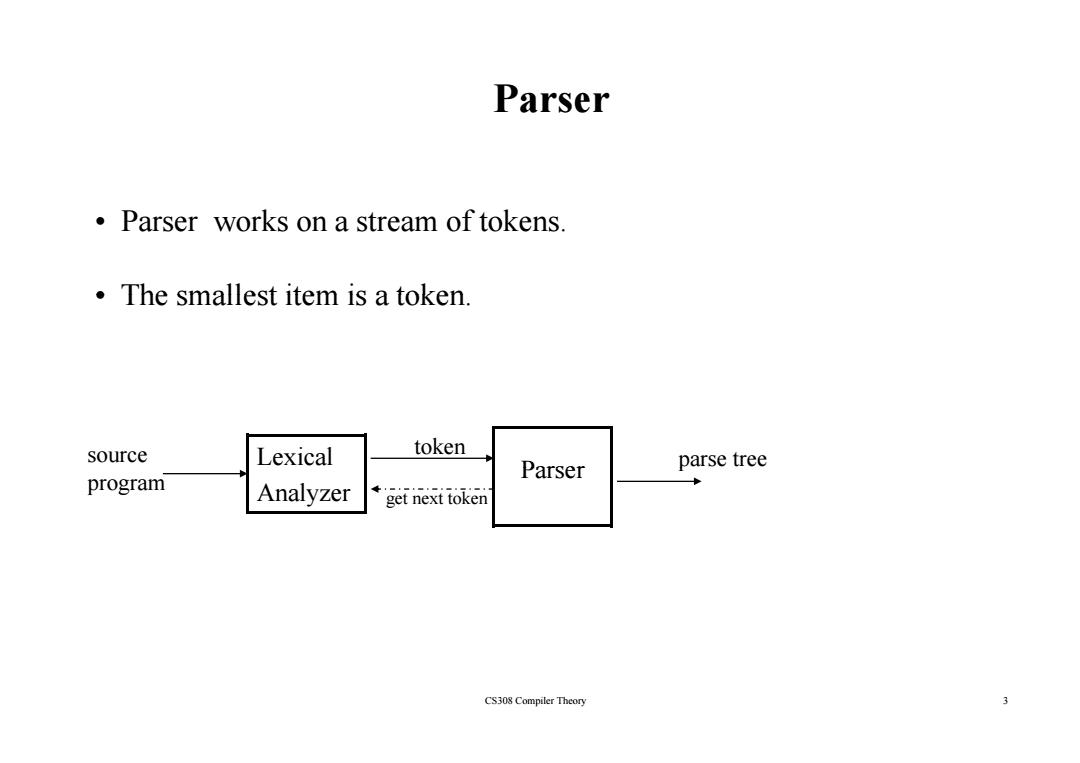
Parser Parser works on a stream of tokens. The smallest item is a token. source Lexical token Parser parse tree program Analyzer get next token CS308 Compiler Theory 3
Parser • Parser works on a stream of tokens. • The smallest item is a token The smallest item is a token. Lexical Parser source token parse tree Analyzer Parser program get next token p CS308 Compiler Theory 3

Parsers (cont.) We categorize the parsers into two groups: 1.Top-Down Parser the parse tree is created top to bottom,starting from the root. 2.Bottom-Up Parser - the parse is created bottom to top;starting from the leaves o Both top-down and bottom-up parsers scan the input from left to right (one symbol at a time). Efficient top-down and bottom-up parsers can be implemented only for sub-classes of context-free grammars. -LL for top-down parsing LR for bottom-up parsing CS308 Compiler Theory 4
Parsers (cont.) • We categorize the parsers into two groups: 1. Top-Down Parser – the parse tree is created top to bottom starting from the root the parse tree is created top to bottom, starting from the root. 2. Bottom-Up Parser – the parse is created bottom to top; starting from the leaves the parse is created bottom to top; starting from the leaves • Both top Both top-down and bottom down and bottom-up parsers scan the input from left to right up parsers scan the input from left to right (one symbol at a time). • Efficient top-down and bottom-upp p y arsers can be implemented only for sub-classes of context-free grammars. – LL for top-down parsing LR f b i CS308 Compiler Theory 4 – LR for bottom-up parsing

Context-Free Grammars Inherently recursive structures of a programming language are defined by a context-free grammar. In a context-free grammar,we have: A finite set of terminals (in our case,this will be the set of tokens) -A finite set of non-terminals (syntactic-variables) A finite set of productions rules in the following form ·A→a where A is a non-terminal and a is a string of terminals and non-terminals (including the empty string) -A start symbol (one of the non-terminal symbol) ·Example: E→E+EIE-E|E*EE/E|-E E→(E) E→id CS308 Compiler Theory 5
Context-Free Grammars • Inherently recursive structures of a programming language are defined b a conte t by a conte x t -free grammar free grammar. • In a context-free grammar, we have: – A finite set of terminals (in our case, this will be the set of tokens) – A finite set of non-terminals (syntactic-variables) – A finite set of productions rules in the following form • A → α where A is a non-terminal and α is a string of terminals and non-terminals (including the empty string) – A start s y ( mbol (one of the non-terminal s y ) mbol ) • Example: E → E + E|E – E|E * E | E/E | E | E / E | - E E → ( E ) E → id CS308 Compiler Theory 5