2.磁通量 穿过磁场中任一曲面的磁感应线条数,称为该曲 面的磁通量,用符号Φ表示。 Φm=B.d心 ①nm=∫B. 3.磁场中的高斯定理 Φm=fB.西 f8.d=0 穿过任意闭合曲面的磁通量为零 ()磁力线是无头无尾的闭合曲线, (2)磁场是无源场-无磁单极存在) 两的肉例
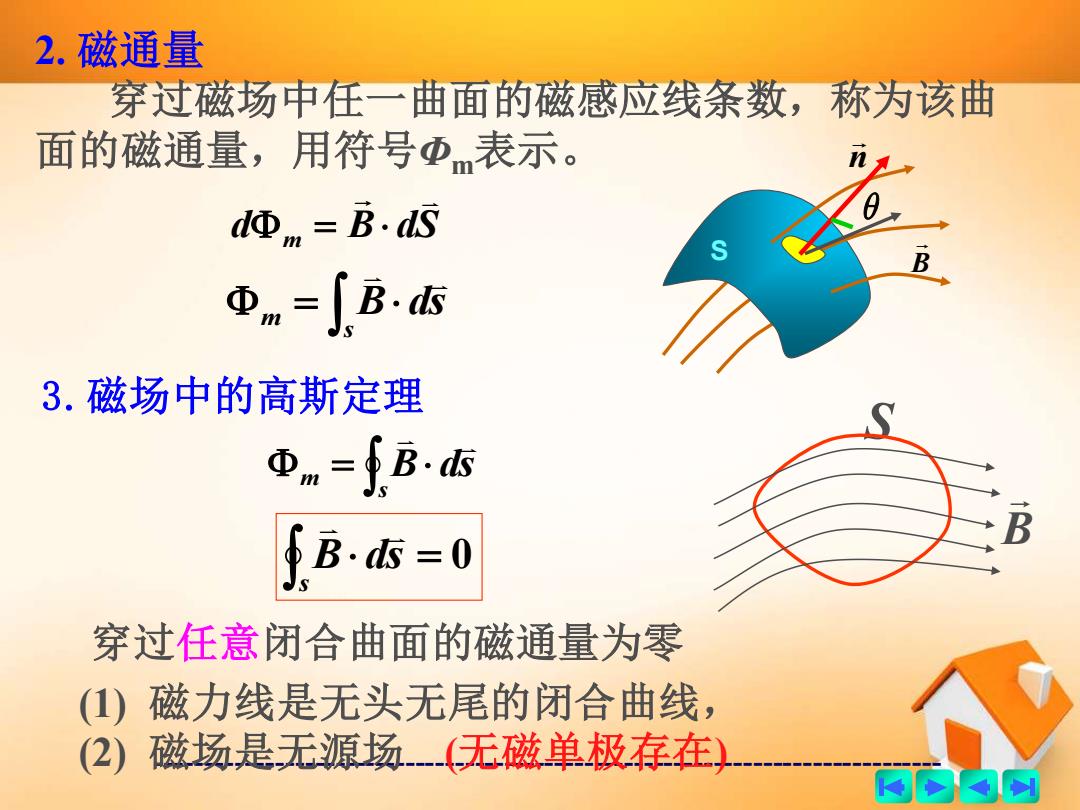
------------------------------------------------------------------------------- 2. 磁通量 穿过磁场中任一曲面的磁感应线条数,称为该曲 面的磁通量,用符号Φm表示。 S B n d m B dS = = s m B ds 3.磁场中的高斯定理 S B = s m B ds = s B ds 0 穿过任意闭合曲面的磁通量为零 (1) 磁力线是无头无尾的闭合曲线, (2) 磁场是无源场 (无磁单极存在)

四、毕奥一萨伐尔定律 1.稳恒电流的磁场 电流元dd dB=k Idlsin(di,r) dB k==10-7TmA1, 4元 Idi 4=4π×10-7T.m,A1 dB的方向dB(dL×) dB=hl×6 毕奥-沙伐尔定律 4π2 粉的厨
------------------------------------------------------------------------------- 四、毕奥—萨伐尔定律 1.稳恒电流的磁场 电流元 Idl I p Idl r dB 2 sin( , ) r Idl dl r dB k = 10 , 4 0 −7 −1 k = = T m A 7 1 0 4 10− − = T m A dB 的方向 dB//(dl r) 2 0 0 4 r Idl r dB = 毕奥---沙伐尔定律
对一段载流导线 B- lIdl× 2 若0=0或元,则dB=0, 即电流元不在自身方向上激发磁场。 若0=元/2,则dB最大(其它因素不变下) 2.运动电荷的磁场 在非相对论条件下的电场与磁场 电流的微观形式 两的内例
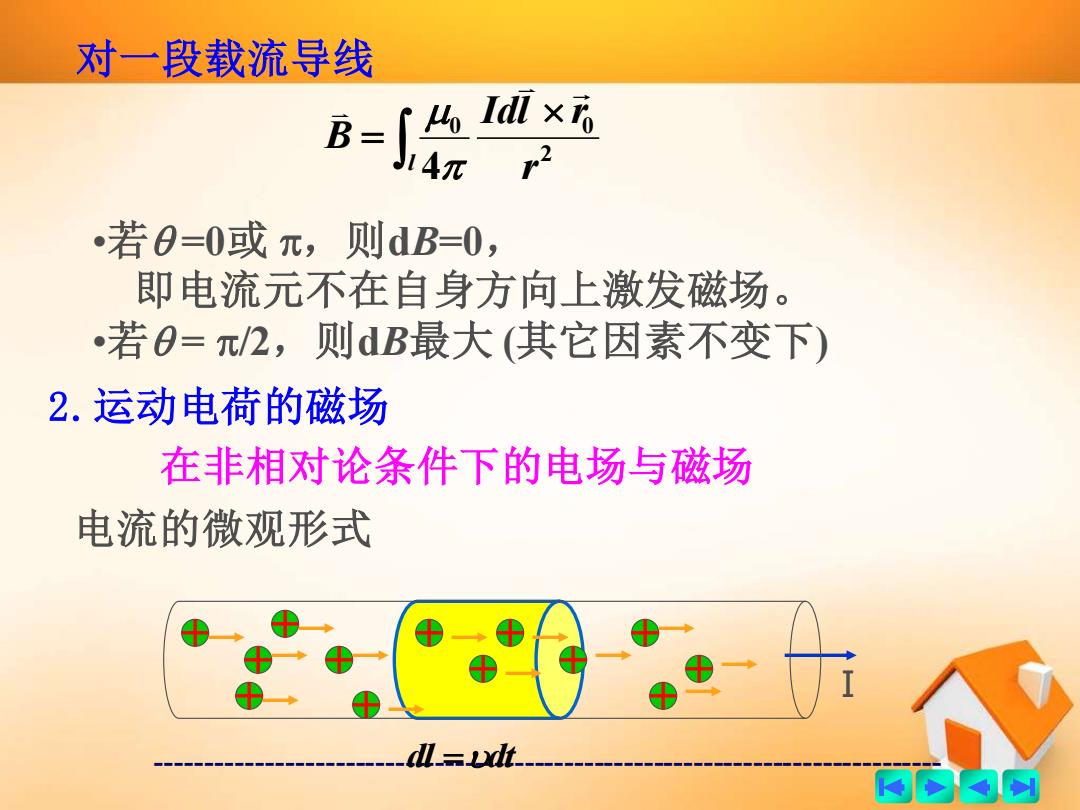
------------------------------------------------------------------------------- 对一段载流导线 2 0 0 4 r Idl r B l = •若 =0或 ,则dB=0, 即电流元不在自身方向上激发磁场。 •若 = /2,则dB最大 (其它因素不变下) 2.运动电荷的磁场 在非相对论条件下的电场与磁场 电流的微观形式 dl =dt I

若载流子的数密度为n,电量为q,运动速度为v 则dt时间内通过s截面的电量 I= do q:n·svat dt dt qnsu dB 4qs·D·l×后=凸4sdD×6 4元 2 4π ~3 电流元Idl中载流子(运动电荷)有dN个 dN=n.sdl=n·svdt B dB 4q(nsll)D× dN 4π dN.r2 B 4qδ×6 毕奥-沙伐尔定 4】 律的微观形式
------------------------------------------------------------------------------- 若载流子的数密度为n,电量为q,运动速度为 ,则dt时间内通过s截面的电量 dt dQ I = dt q n sdt = = qns 2 0 0 4 r qns dl r dB = 2 0 0 4 r qnsdl r = 电流元Idl中载流子(运动电荷)有 dN个 dN = nsdl = nsdt dN dB B = 2 0 0 4 dN r q nsdl r = ( ) 2 0 0 4 r q r B = 毕奥-沙伐尔定 律的微观形式
B B 的内网
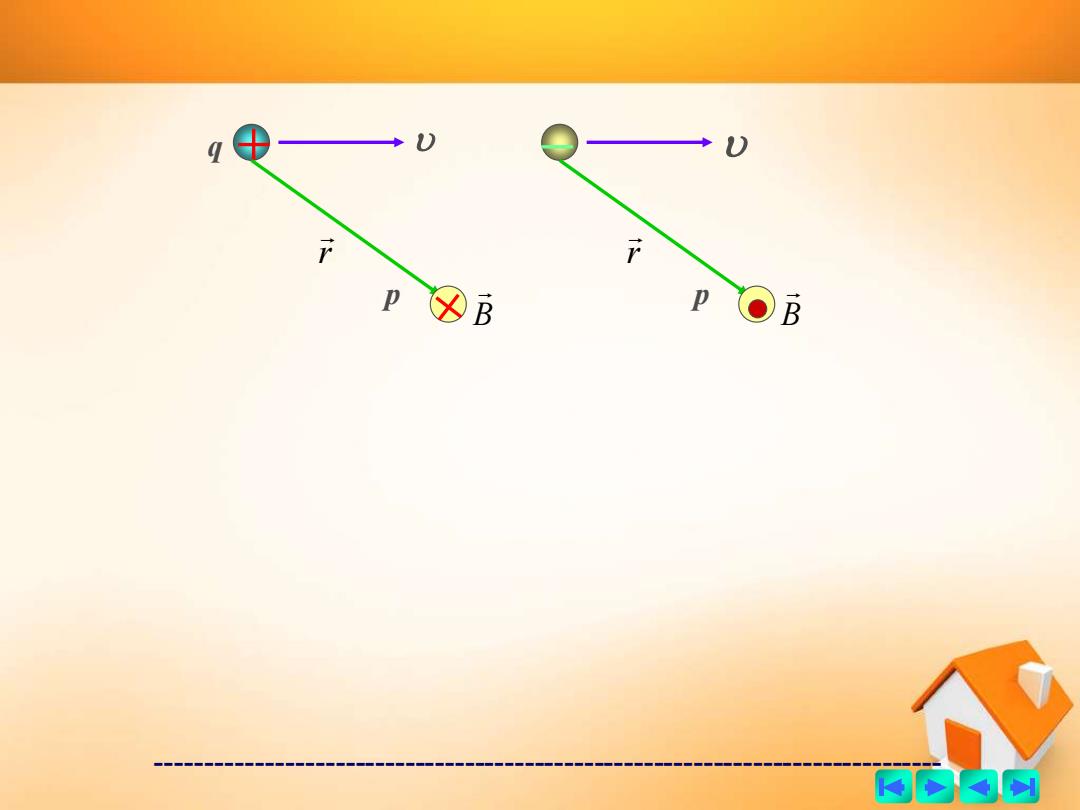
------------------------------------------------------------------------------- B q p r B p r