电子科技大学：《振动理论与声学原理 Vibration and Acoustics》课程教学资源（课件讲稿）第四章 多自由度系统的振动

一、多自由度系统的动力学方程 刚度矩阵和质量矩阵 例题如图系统。写出M、K及运动微分方程。 & →(t0 k w w (t) 解：先确定刚度矩阵K。 →(% B w -w w 考虑静态，即不产生加速度。 令x=[100 当m1上产生单位 位移时P1(①的值 P(t) 0 P(t) P(t)= P(t) 0 P,(t) P(t)= P(t) P.(t)

21 解： 考虑静态，即不产生加速度。 令   T X  1 0 0 例题 如图系统。写出 M 、 K 及运动微分方程。                            nj j j n nj nn j n j n n k k k k k k k k k k k k P t P t P t t     2 1 1 21 2 2 11 1 1 2 1 0 0 1 0 0 ... ... ..................... ... ... ... ... ( ) ( ) ( ) P( ) 1 11 2 21 3 31 ( ) ( ) ( ) ( ) P t k t P t k P t k                   P 当m1上产生单位 位移时P1(t)的值 先确定刚度矩阵K

一、多自由度系统的动力学方程 刚度矩阵和质量矩阵 受力分析 P1(t) K m K2 故 k11=k1+k2 k21=-k2 k31=0 令X=[01 k2=-k2k2=k2+k3+k+k6k32=-k3 令X=[00 → k13=0 k23=-k3 k3=k3+k4 k+k2 -k2 0 刚度矩阵： K= -k2k2+k3+k+k6 -k3 22 -k3 k3+k4」

22 令   T X  0 1 0 令   T X  0 0 1 12 2 k  k 22 2 3 5 6 k  k  k  k  k 32 3 k  k k13  0 23 3 k  k 33 3 4 k  k  k 刚度矩阵：                 3 3 4 2 2 3 5 6 3 1 2 2 0 0 k k k k k k k k k k k k K m1 K1 K2 P1(t) 21 2 k  k 0 k31  受力分析 11 1 2 故 k  k  k

一、多自由度系统的动力学方程 刚度矩阵和质量矩阵 例3如图系统。写出M、K及运动微分 ◆P(t) 方程。 6 w w 解：确定质量矩阵 P (D →P(t) w 考虑动态，即不产生位移。 令=[00]y 有： m11=m1 m21=0 m31=0 令=[010 有： m12=0 m22=m2 m32=0 令求=[001] 有： m3=0 m23=0 m33=m3 m 0 0 质量矩阵： M= 0 m2 0 运动微分方程： 0 0 m m 0 k+k2 一k2 0 P() 0 m 0 2 + -k2 k2+k3+ks+ko -k3 X2 = B() 0 0 0 -k3 P(县 M戊+X=P(t)

23 令   T X  1 0 0  m11  m1 0 有： m21  m31  0 令   T X  0 1 0  m12  0 有： m22  m2 m32  0 令   T X  0 0 1  m13  0 m23  0 有： m33  m3 质量矩阵：        3 2 1 0 0 0 0 0 0 m m m M 解：确定质量矩阵 考虑动态 ，即不产生位移。 例3 如图系统。写出 M 、 K 及运动微分 方程。                                          ( ) ( ) ( ) 0 0 0 0 0 0 0 0 3 2 1 3 2 1 3 3 4 2 2 3 5 6 3 1 2 2 3 2 1 3 2 1 P t P t P t x x x k k k k k k k k k k k k x x x m m m    运动微分方程： MX  KX  P(t) 

知识回顾 MX+KX=P(t) 作用力方程 结论：刚度矩阵K中的元素k的物理意义：是使系统仅在第 j个坐标上产生单位位移而相应于第i个坐标上所需 施加的力 结论：质量阵M中的元素m防 是系统为仅在第个坐标上产生 单位加速度而在第个坐标上所需施加的外力。 24

24 M X  K X  P(t)  作用力方程 结论：刚度矩阵K中的元素kij的物理意义：是使系统仅在第 j 个坐标上产生单位位移而相应于第 i 个坐标上所需 施加的力 。 结论：质量阵M 中的元素mij 是系统为仅在第j 个坐标上产生 单位加速度而在第i个坐标上所需施加的外力。 知识回顾

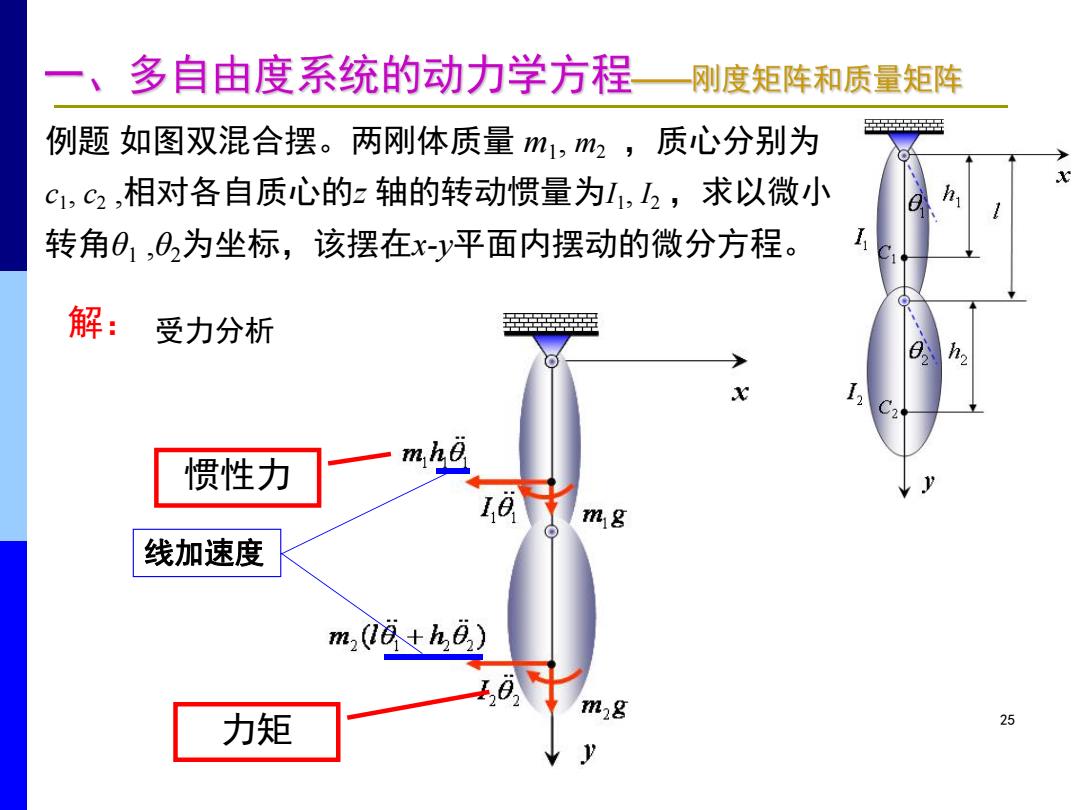
一、多自由度系统的动力学方程 —刚度矩阵和质量矩阵 例题如图双混合摆。两刚体质量m1,m2, 质心分别为 蛋 C1,c2,相对各自质心的z轴的转动惯量为，，求以微小 x h 转角01,02为坐标，该摆在x-y平面内摆动的微分方程。 解：受力分析 a h2 x 惯性力 m.h y mg 线加速度 m08+h8) 力矩 m2g 25

25 例题 如图双混合摆。两刚体质量 m1 , m2 ，质心分别为 c1 , c2 ,相对各自质心的z 轴的转动惯量为I1 , I2 ，求以微小 转角θ1 ,θ2为坐标，该摆在x-y平面内摆动的微分方程。 解： 受力分析 惯性力 力矩 线加速度