电子科技大学：《振动理论与声学原理 Vibration and Acoustics》课程教学资源（课件讲稿）第四章 多自由度系统的振动

一、多自由度系统的动力学方程 刚度矩阵和质量矩阵 求质量影响系数 动量矩平衡 令6=1,62=0有： mh mz m2lh2 m1=11+m,h2+m,1+h)-m21=1+m,h2+m212 m21+h点) 1, 令6=0,6，=1有： m2g m2=12+m2h2 m12=I2+m2h2(1+h2)-m22=m2lh2 质量矩阵： 8=1 =0 a2=0 =1

26 令 1 1 2  0  ，  2 2 2 2 2 21 1 1 1 2 11 1 1 1 21 2 2 m I m h m l(l h ) m I m h m l m m lh          有： 令 1  0 2 1  ，  12 2 2 2 2 22 2 2 2 22 2 2 2 m I m h (l h ) m m lh m I m h        有： 求质量影响系数           2 2 2 2 2 2 2 2 2 2 2 1 1 1 m lh I m h I m h m l m lh M 质量矩阵： 动量矩平衡

一、 多自由度系统的动力学方程 刚度矩阵和质量矩阵 求刚度影响系数 力矩平衡 苹 令0=1,02=0 有： k e mgh sine +mglsink=migh +m2gl k2181=m2gl*0 k21=0 令0，=0,02=1 有： m2g m2g k22 m2 ghz kv2 =m2gh2 -k22 =0 8=1 8=0 82=0 62=1 刚度矩阵： 0 27 m2gh2」

27 令 1 1， 2  0 令 1  0， 2 1 22 2 2 k  m gh k12  m2 gh2  k22  0 有： 求刚度影响系数 刚度矩阵：         2 2 1 1 2 0 ( ) 0 m gh m h m l g K 力矩平衡 有： 11 1 1 1 1 2 1 k   m gh sin  m glsin 21 1 2 k   m gl 0 0 k21  k m gh m gl 11  1 1  2

一、多自由度系统的动力学方程 刚度矩阵和质量矩阵 蛋 h m2lh2 12+m,h2 0 e h2 运动微分方程： L1+m,h2+m,12, m21h2 28

28 0 0 ( ) 0 2 1 2 2 1 1 2 2 1 2 2 2 2 2 2 2 2 2 2 2 1 1 1                                  m gh m h m l g m lh I m h I m h m l m lh   运动微分方程：           2 2 2 2 2 2 2 2 2 2 2 1 1 1 m lh I m h I m h m l m lh M         2 2 1 1 2 0 ( ) 0 m gh m h m l g K

知识回顾 MX+KX=P(t) 作用力方程 结论：刚度矩阵K中的元素k的物理意义：是使系统仅在第 j个坐标上产生单位位移而相应于第i个坐标上所需 施加的力 结论：质量阵M中的元素m防 是系统为仅在第个坐标上产生 单位加速度而在第个坐标上所需施加的外力。 29

29 M X  K X  P(t)  作用力方程 结论：刚度矩阵K中的元素kij的物理意义：是使系统仅在第 j 个坐标上产生单位位移而相应于第 i 个坐标上所需 施加的力 。 结论：质量阵M 中的元素mij 是系统为仅在第j 个坐标上产生 单位加速度而在第i个坐标上所需施加的外力。 知识回顾

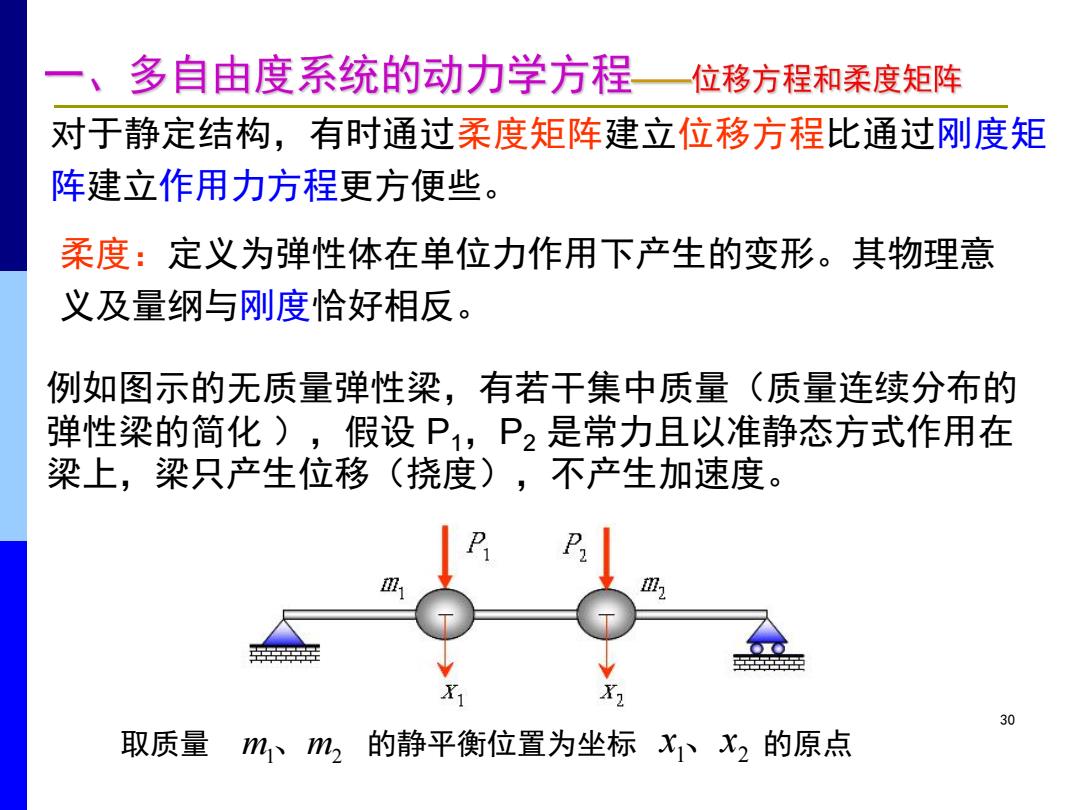
一、多自由度系统的动力学方程 位移方程和柔度矩阵 对于静定结构，有时通过柔度矩阵建立位移方程比通过刚度矩 阵建立作用力方程更方便些 柔度：定义为弹性体在单位力作用下产生的变形。其物理意 义及量纲与刚度恰好相反。 例如图示的无质量弹性梁，有若干集中质量（质量连续分布的 弹性梁的简化)，假设P1,P2是常力且以准静态方式作用在 梁上，梁只产生位移（挠度），不产生加速度。 迎1 岳 ●● 30 取质量 mm2的静平衡位置为坐标XX2的原点

30 对于静定结构，有时通过柔度矩阵建立位移方程比通过刚度矩 阵建立作用力方程更方便些。 柔度：定义为弹性体在单位力作用下产生的变形。其物理意 义及量纲与刚度恰好相反。 m1、m2 1 2 取质量 的静平衡位置为坐标 x、x 的原点 例如图示的无质量弹性梁，有若干集中质量（质量连续分布的 弹性梁的简化 ），假设 P1，P2 是常力且以准静态方式作用在 梁上，梁只产生位移（挠度），不产生加速度