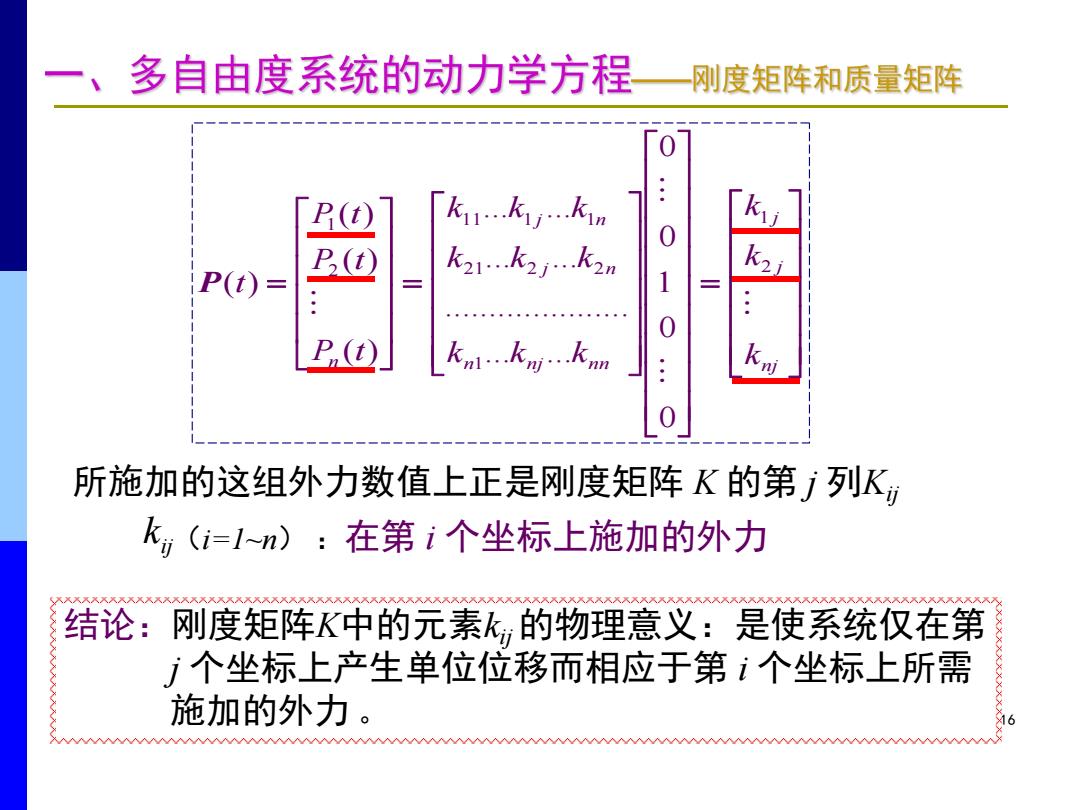
一、多自由度系统的动力学方程 刚度矩阵和质量矩阵 (t) P(t) k2i P(t)= 0 P,( 所施加的这组外力数值上正是刚度矩阵K的第j列K k,(i=l~n):在第i个坐标上施加的外力 结论:刚度矩阵K中的元素k的物理意义:是使系统仅在第 j个坐标上产生单位位移而相应于第i个坐标上所需 施加的外力
16 nj j j n nj nn j n j n n k k k k k k k k k k k k P t P t P t t 2 1 1 21 2 2 11 1 1 2 1 0 0 1 0 0 ... ... ..................... ... ... ... ... ( ) ( ) ( ) P( ) 结论:刚度矩阵K中的元素kij的物理意义:是使系统仅在第 j 个坐标上产生单位位移而相应于第 i 个坐标上所需 施加的外力 。 所施加的这组外力数值上正是刚度矩阵 K 的第 j 列Kij kij(i=1~n) :在第 i 个坐标上施加的外力

一、多自由度系统的动力学方程 刚度矩阵和质量矩阵 作用力方程 MX+KX=P(t) X∈Rm 质量矩阵M 假设系统受到外力作用的瞬时,只产生加速度而不产生任何位移 即:X=0 则有:M戊=P(t) 假设作用于系统的是这样一组外力,它们使系统只在第个坐标上产生 单位加速度,而在其他各个坐标上不产生加速度。即: X=[31,,j-1,1,j41…,8n]Y=[0,…,0,1,0,,0] 代入:MX=P(t) 17
17 n MX KX P(t) X R 质量矩阵 M 假设系统受到外力作用的瞬时,只产生加速度而不产生任何位移 即: X = 0 MX P(t) 则有: 作用力方程 假设作用于系统的是这样一组外力,它们使系统只在第 j 个坐标上产生 单位加速度,而在其他各个坐标上不产生加速度。即: 1 1 1 [ ,..., , , ,..., ] [0,...,0,1,0,...,0] T T j j j n x x x x x X 代入 : MX P(t)

一、 多自由度系统的动力学方程 刚度矩阵和质量矩阵 P( m11.m1.m1m P(t) m1... m2j P() 使系统只在第个坐标上产生单位加速度,而在其他坐标上不产生加速度 所施加的一组外力,正是质量矩阵M的第列。 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX XXXXXX 结论:质量阵M中的元素m, 是系统为仅在第个坐标上产生 单位加速度而在第个坐标上所需施加的外力。 M)k,又分别称为质量影响系数和刚度影响系数。 18 根据它们的物理意义可以直接写出矩阵M和K,从而建立作用力方程 这种方法称为影响系数方法
18 使系统只在第j 个坐标上产生单位加速度,而在其他坐标上不产生加速度 所施加的一组外力,正是质量矩阵M 的第j 列。 结论:质量阵M 中的元素mij 是系统为仅在第j 个坐标上产生 单位加速度而在第i个坐标上所需施加的外力。 mij、ij k 又分别称为质量影响系数和刚度影响系数。 根据它们的物理意义可以直接写出矩阵 M 和 K,从而建立作用力方程, 这种方法称为影响系数方法 。 nj j j n nj nn j n j n n m m m m m m m m m m m m P t P t P t t 2 1 1 21 2 2 11 1 1 2 1 0 0 1 0 0 ... ... ..................... ... ... ... ... ( ) ( ) ( ) P( )

多自由度系统振动方程的确定【PDF】 19
19

一、多自由度系统的动力学方程 刚度矩阵和质量矩阵 例题如图系统。写出M、K及运动微分方程。 B(t) 6 (t P (D) w 结论:刚度矩阵K中的元素k,的物理意义:是使系统仅在第 j个坐标上产生单位位移而相应于第i个坐标上所需 施加的外力 结论:质量阵M中的元素m, 是系统为仅在第个坐标上产 生单位加速度而在第个坐标上所需施加的外力。 XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX 20
20 例题 如图系统。写出 M 、 K 及运动微分方程。 结论:刚度矩阵K中的元素kij的物理意义:是使系统仅在第 j 个坐标上产生单位位移而相应于第 i 个坐标上所需 施加的外力 。 结论:质量阵M 中的元素mij 是系统为仅在第j 个坐标上产 生单位加速度而在第i个坐标上所需施加的外力