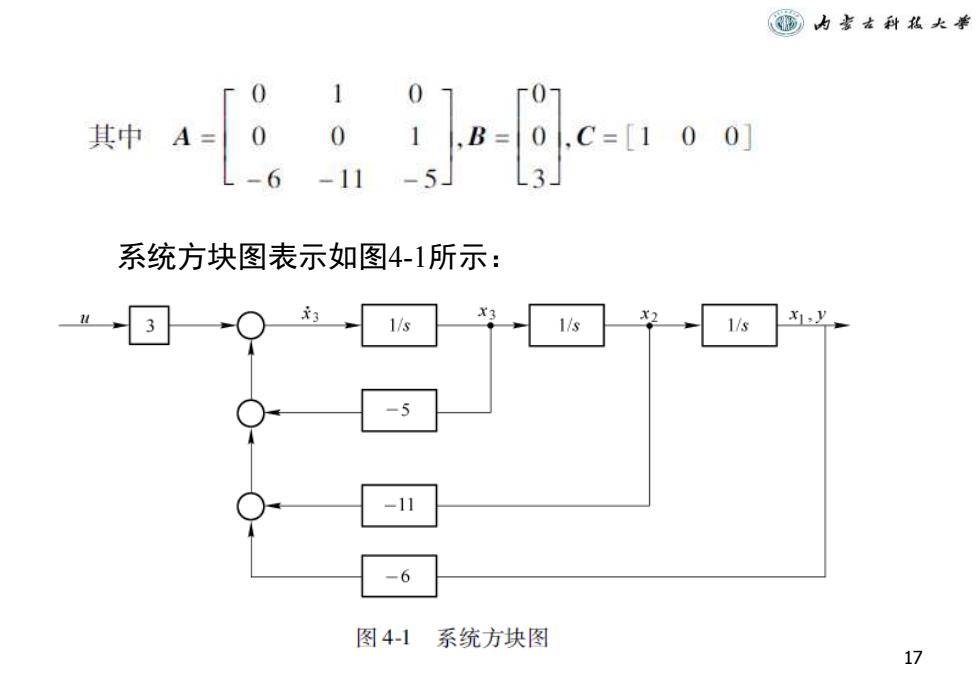
内喜古科私大拳 1 0 Γ01 t> 0 1,B= 0. C=[100] -11-5 系统方块图表示如图4-1所示: 1/s 1/s 1/s -5 -11 -6 图4-1系统方块图 17
17 系统方块图表示如图4-1所示:
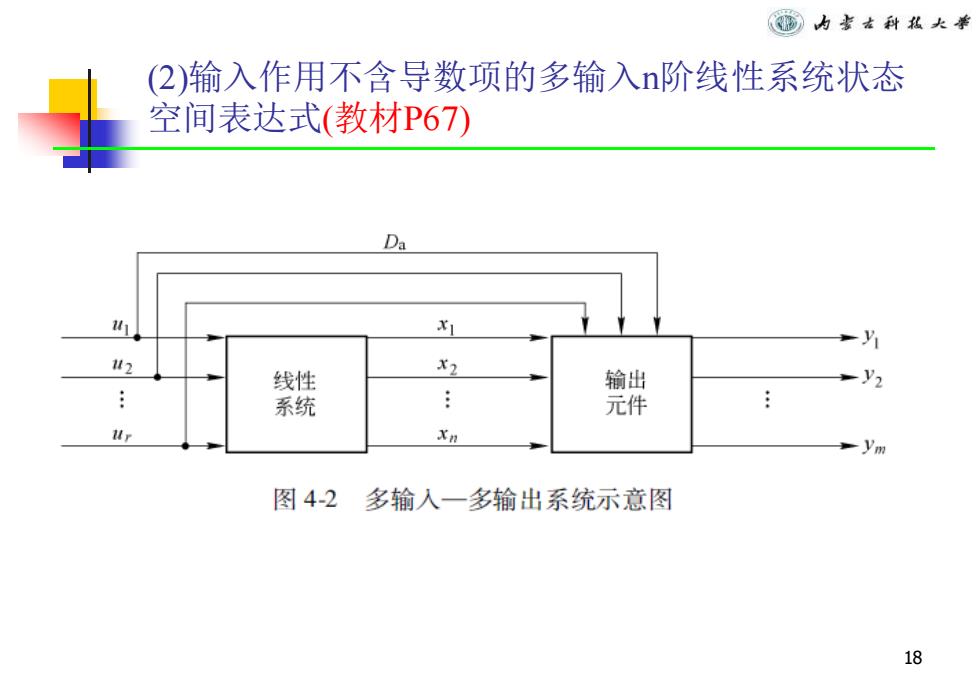
窗内害古科私大举 (2)输入作用不含导数项的多输入n阶线性系统状态 空间表达式(教材P67) Da 12 线性 X2 输出 系统 元件 Xn ym 图4-2多输入一多输出系统示意图 18
18 (2)输入作用不含导数项的多输入n阶线性系统状态 空间表达式(教材P67)
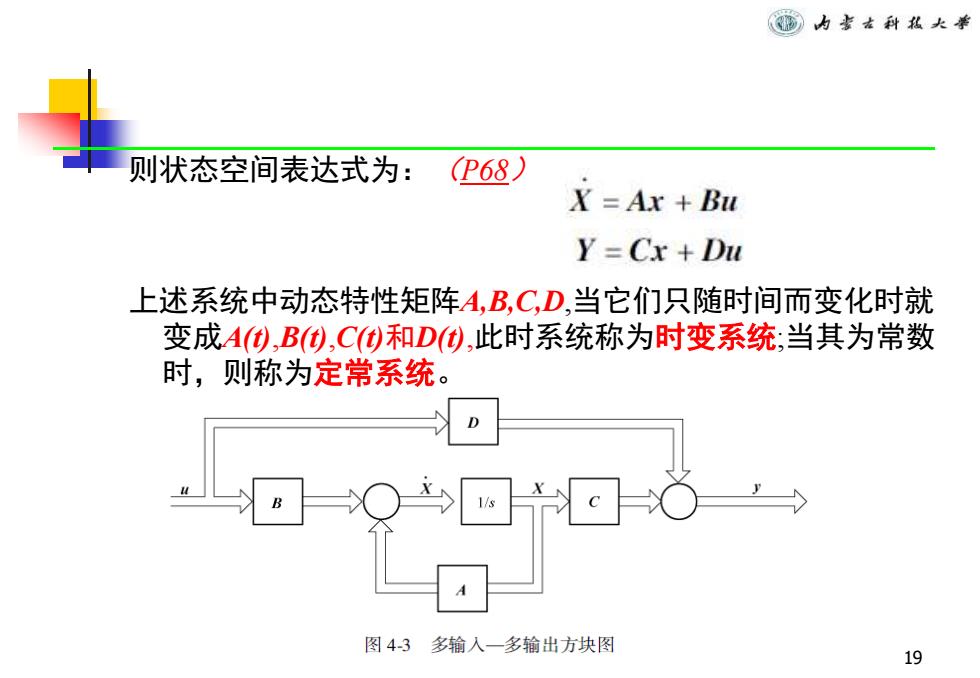
内古科私大举 则状态空间表达式为: (P68) X=Ax Bu Y=Cx+Du 上述系统中动态特性矩阵A,B,C,D,当它们只随时间而变化时就 变成A(①,B(,C0和D(,此时系统称为时变系统;当其为常数 时,则称为定常系统。 D 图4-3多输人一多输出方块图 19
19 则状态空间表达式为:(P68) 上述系统中动态特性矩阵A,B,C,D,当它们只随时间而变化时就 变成A(t),B(t),C(t)和D(t),此时系统称为时变系统;当其为常数 时,则称为定常系统

窗内害古科私大举 ●状态方程的解及转移矩阵 在建立控制系统的状态空间表达式后,更需要的是确定 系统在时间域中的解。 本节先介绍连续型线性定常系统中齐次与非齐次方程的 解法,然后引出状态转移矩阵的重要概念。 状态方程的解与微分方程解非常相似,其全解包括通解与 特解两个部分。 20
20 ●状态方程的解及转移矩阵 在建立控制系统的状态空间表达式后,更需要的是确定 系统在时间域中的解。 本节先介绍连续型线性定常系统中齐次与非齐次方程的 解法,然后引出状态转移矩阵的重要概念。 状态方程的解与微分方程解非常相似,其全解包括通解与 特解两个部分

《内右科私大举 (1)线性定常系统齐次状态方程的解法 连续型系统的求解方法很多,此只介绍拉氏变换法和级 数法。(见教材P69, x(t)=e“x(0) (4-19) 综上(1)(2)中(式4-14)和(式4-19)所述,可将线性 定常系统齐次方程的解写成: x(t)=(t)x(0) (4-20) 式中:p()=eAt=L-1[(s一A)-] (4-21) 21
21 (1)线性定常系统齐次状态方程的解法 连续型系统的求解方法很多,此只介绍拉氏变换法和级 数法。(见教材P69) 综上(1)(2)中(式4-14)和(式4-19)所述,可将线性 定常系统齐次方程的解写成 : x(t)= φ(t)·x(0) 式中:φ(t)= eAt = L-1 [(sI-A)-1 ] (4-19) (4-20) (4-21)