上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 7_chap7-Numerical Methods in Dynamics

7.2 Mixed differential-algebraic equations M Dynamic equations 9 Kinematic constraint equations Φ(q)=0Φ，9=v Comprise the mixed differential-algebraic equations of motion

7.2 Mixed differential-algebraic equations Dynamic equations                    M  q Q q q  0 T Kinematic constraint equations (q)  0 q v  q   Comprise the mixed differential-algebraic equations of motion

7.3 Proposed solution methods for Mixed differential- algebraic equations 1.Coordinates partitioning v:Independent coordinates g= u:coordinates dependent on v u=f(v) 功，=[ Φ] Φ4=V Φ，i=Y Φi+Φ=VΦi+Φ，i=Y In case that is nonsingular i=Φw(V-Φ) i=Φ(y-更)

7.3 Proposed solution methods for Mixed differential- algebraic equations        v u q u  q   u  v   qq V  q   q   uu  v v V  u  v   u v   ( ) 1 u V v u v      ( ) 1 u v u v       u  f (v)

We can write M+Φ，=24 M as 如百®-8 (1) M Substitute i=Φn(y-Φ into equation (1) and eliminate M节=9 Where i=M"-M“D..-,7画.Y(M"-M"电.'，） 2=g-M"更.y-更西yg-Mm中.y）

( ) 1 u v u v       T A Mq q   Q                          Av Au T T vu vv uu uv Q Q v u M M M M v u      M ˆ v Q ˆ       M M M  u  v  v  u M M  u  v 1 1 1 ˆ        uv uu T vv vu T          1 1 1 ˆ    Q  Q  M u  v u Q  M u Au uu T Av vu T

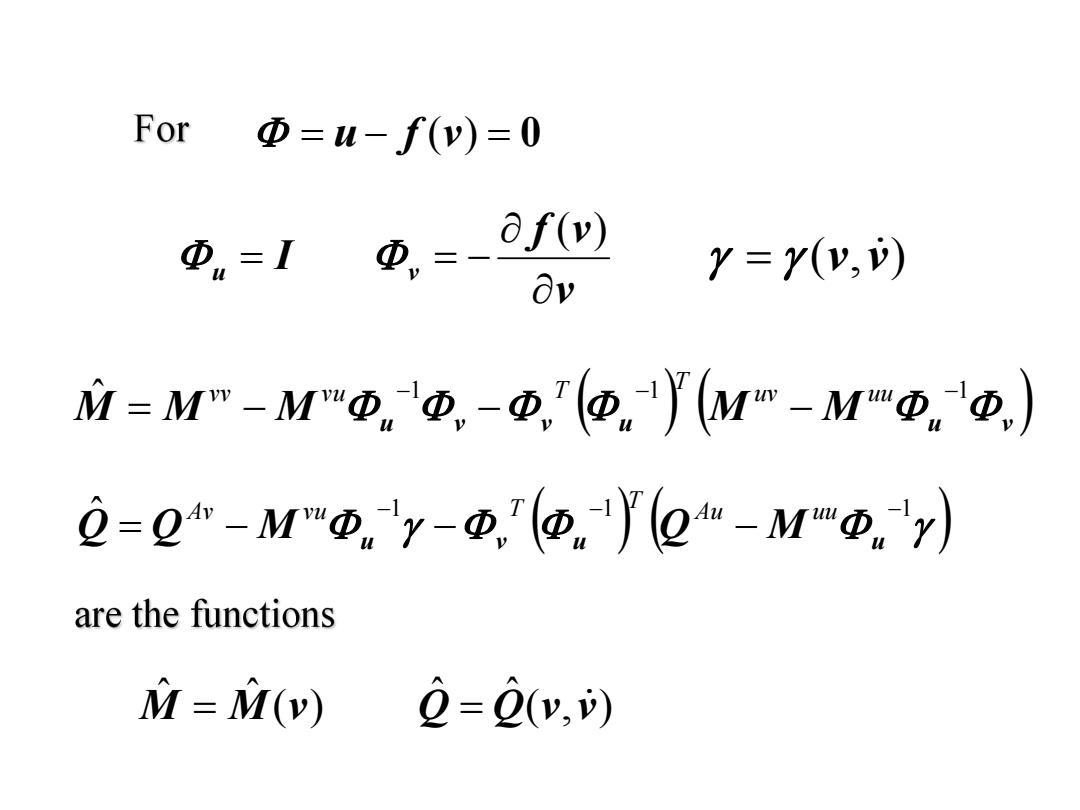
For Φ=u-f(v)=0 D=1D= of(v) Y=Y(v,v) Ov =M"-MmD.更，-更，西，y(Mm-M中.'o） ⑨=0-M更，y-更，西.y但-MΦy） are the functions M=M(v) 0=0(,)

  u  f (v)  0 I  u      M M M  u  v  v  u M M  u  v 1 1 1 ˆ        uv uu T vv vu T          1 1 1 ˆ    Q  Q  M u  v u Q  M u Au uu T Av vu T v f v v     ( )  ( ) ˆ ˆ M  M v ( , ) ˆ ˆ Q  Q v v    (v,v)

Step 1: For t=0v(0),(0) are given Solve u(0)=f(v(0) a(0)=af(0)0) 〉 (0),(0) Step 2: Solve M节=Q i =M-Q Step 3: Let S=V,P=少 5=r,r=M0 Integrate for one time step s(to)=v(to),r(to)=v(to)

( ) ( ), ( ) ( ) ˆ ˆ , 0 0 0 0 1 s t v t r t v t s r r M Q         M ˆ v Q ˆ   v Mˆ 1Qˆ   s v,r v 0 t0  v(0), v(0) u(0)  f (v (0)) (0) (0) ( ) (0) v v f v u     u(0), u(0)