中国科学技术大学：《束流光学》课程教学资源（PPT课件讲稿）第五章 宽束和强流电子学简介

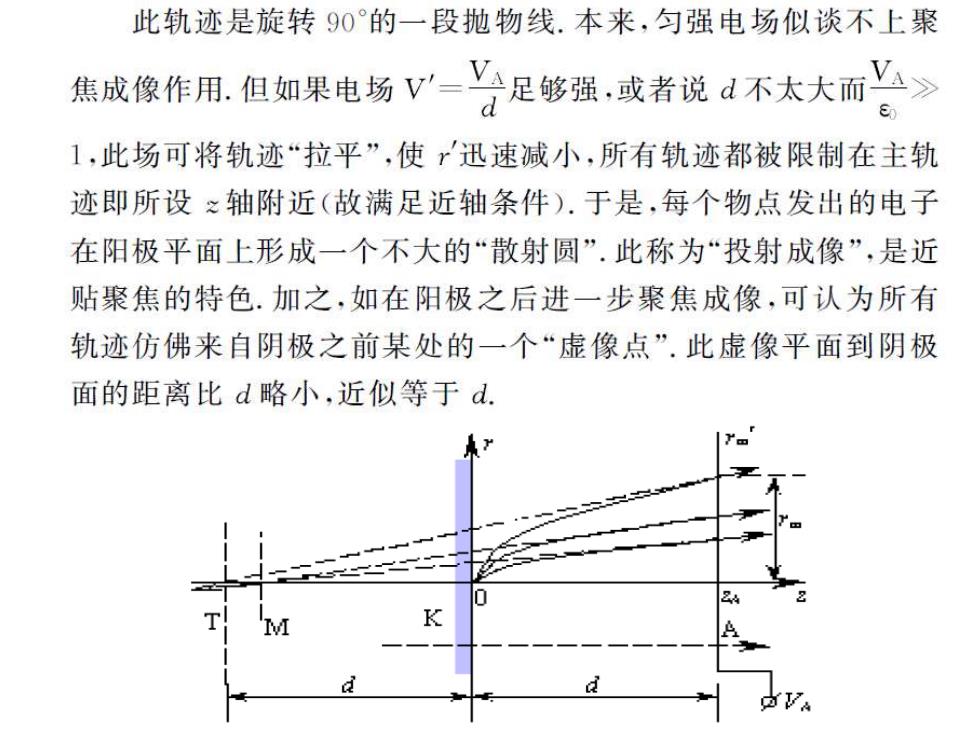
此轨迹是旋转90°的一段抛物线.本来，匀强电场似谈不上聚 焦成像作用，但如果电场V”学足够强，或者说d不太大而亡> 1,此场可将轨迹“拉平”，使迅速减小，所有轨迹都被限制在主轨 迹即所设之轴附近（故满足近轴条件）.于是，每个物点发出的电子 在阳极平面上形成一个不大的“散射圆”.此称为“投射成像”，是近 贴聚焦的特色.加之，如在阳极之后进一步聚焦成像，可认为所有 轨迹仿佛来自阴极之前某处的一个“虚像点”.此虚像平面到阴极 面的距离比d略小，近似等于d. a

d_ =d (V(e)+e)儿 4头防 :V"=0 -西d-y小，卧 :V(0)=0,r(0)=0→C=Ve@=V@ V-o V(=)+6.)r=V5 v日间- →r=VE +可后- VA VVA 在一d附近.主轨迹有Ve,=0,=0,就是之轴，无须讨论

2 2 1 A r z z r z z A A A A d V r z d V d V V V           = + − = + −         ( ( ) )( ( ( ) ) ) ( ( ( ) ) ) ( ( ) ) ( ) ( ) ( ( ) ) ( ( ) ) ( ) 0 0 0 0 0 0 0 0 1 0 4 0 0 0 0 0 1 d 1 1 2 2 d d z z z z r r z r z z z r z r z A z z z A A r r r z r z z A A A A z z V z V z r V r V V z r V z r C v v V r C v v V z r r z V z V V z z d d d V V r z z z z V V V d V d z z d d                     + + + =    =   + =  + =     = =  + =  = + =     = = = + = + −             + +        ＝ ， ＝      2 2 2 2 1 1 1 r A z z A A z A z z r A A z z z z z z A A A A A d V r d V d d d V V r V V d d d V V V V V                + −   − = − = − + + −      +     = − + + − = − + −        

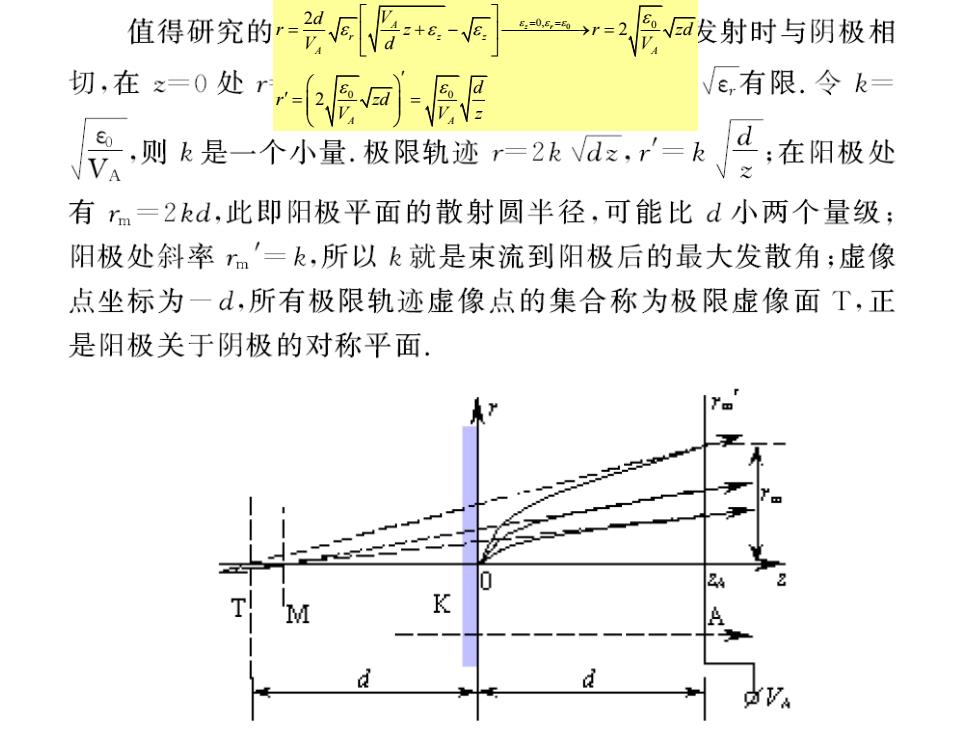
值得研究的侣* -2发射时与阴极相 切在=0处r回j-辰目 Ve,有限.令k= 侵则是一个小量，极限轨迹一2kV,-及 'd ;在阳极处 有rm=2kd,此即阳极平面的散射圆半径，可能比d小两个量级； 阳极处斜率m'=k,所以k就是束流到阳极后的最大发散角；虚像 点坐标为一d,所有极限轨迹虚像点的集合称为极限虚像面T,正 是阳极关于阴极的对称平面

0 0 , 0 0 0 2 2 2 A z r r z z A A A A d V r z r zd V d V d r zd V V z          = =   = + − ⎯⎯⎯⎯→ =         = =      

近贴聚焦过程不改变粒子的横向动量，与一般的成像不同，各 轨迹的虚像点并不重合.其投射成像的单向放大率M,恒为1.也 可如前文一样讨论其像差，即认为散射圆的大小、虚像位置的差 距、虚像平面上“弥散圆”的大小来自像差.如果场是理想均匀场， 每个物点都可看作轴上的点，无所谓“轴外像差”，只有轴上像差， 包括因不同的色差与因初速度角，不同的球差.可以用ε. cos20和e,=osin0代入以上各式，分别讨论这两种像差.也可 合并之，称为色球差，以k的幂次分为一阶、二阶.阳极平面散射圆 的半径是一阶色球差.称虚像点沿轴的散开为纵向色球差，其一阶 项也与kd同量级.称各轨迹反向延长线在虚像平面上构成的弥 散圆半径为横向色球差，它与kd同量级，数值更小.理论上可推 算出（过程略）：在极限虚像面上，弥散圆半径来自(=士于的轨 迹，此半径等于kd:在其附近（见图5.2）有弥散圆半径最小的最 佳虚像面M,该处弥散圆半径为0.6kd

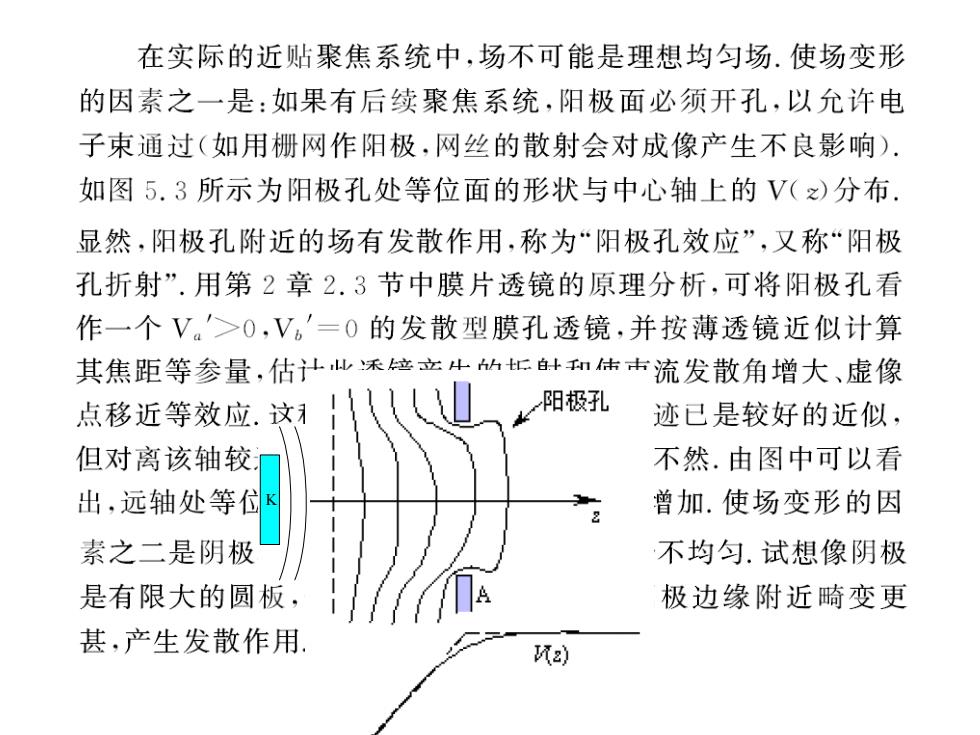
在实际的近贴聚焦系统中，场不可能是理想均匀场.使场变形 的因素之一是：如果有后续聚焦系统，阳极面必须开孔，以允许电 子束通过（如用栅网作阳极，网丝的散射会对成像产生不良影响）. 如图5.3所示为阳极孔处等位面的形状与中心轴上的V(z)分布. 显然，阳极孔附近的场有发散作用，称为“阳极孔效应”，又称“阳极 孔折射”.用第2章2.3节中膜片透镜的原理分析，可将阳极孔看 作一个V。'>0,V。'=0的发散型膜孔透镜，并按薄透镜近似计算 其焦距等参量，估汁此禾座立小h针n估击流发散角增大、虚像 点移近等效应.这 阳极孔 迹已是较好的近似， 但对离该轴较， 不然.由图中可以看 出，远轴处等付 曾加.使场变形的因 素之二是阴极 不均匀.试想像阴极 是有限大的圆板， 极边缘附近畸变更 甚，产生发散作用 风)

K