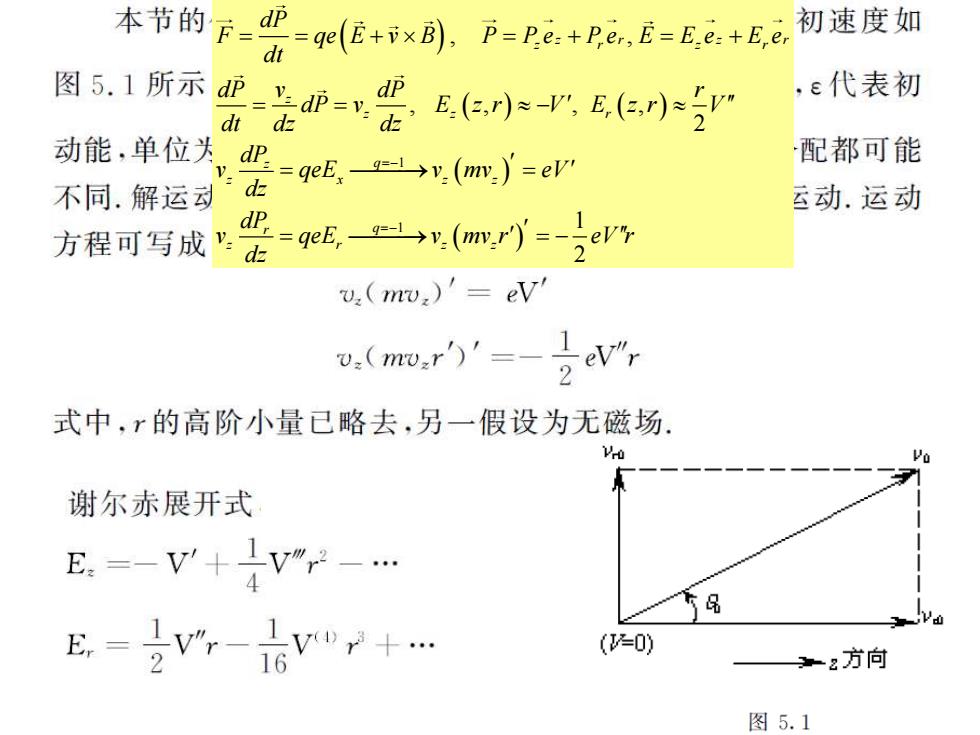
本打的F-四(,Pa+e8上-Ea+6 初速度如 图51所示熙是n=要Ee小B(e小空 e代表初 dt dz 动能.单位关d迟=geE,en(m)=er 配都可能 不同.解运司正 运动.运动 方程可写成竖=E山(m=r v:(mv:)'=ev! .(mr'=-2eW 式中,r的高阶小量已略去,另一假设为无磁场 谢尔赤展开式 E.=-V'+}Vr-… E,=2V-6vw+… (2=0) 32方向 图5.1
( ) ( ) ( ) ( ) ( ) 1 1 , , , , , , 2 1 2 z r z r z r z r z z z r z q z x z z r q z r z z dP F qe E v B P P e P e E E e E e dt dP dP r v dP v E z r V E z r V dt dz dz dP v qeE v mv eV dz dP v qeE v mv r eV r dz = − = − = = + = + = + = = − = ⎯⎯⎯→ = = ⎯⎯⎯→ = −

V. 2er(e)+e)】 u(mr)=-er 前一式是纷 注意:在阴日+e)+r=0 x心J始条件」 代入后一式,得 W+e(W+r')'+}V=0 上式即所谓“近轴轨迹方程”. 和旁轴轨迹方程(高斯轨迹方程)对比: V(,')'+V=0
( ) ( ) ( ) ( ) ( ( ) ) 0 0 2 0 0 2 2 0 2 0 0 0 0 0 d d 2 2 2 2 2 2 z z z z v V z e m v z z e m z z z m v v e V v e eV z m eV z v m m eV z e e v V z m m m = = − = = + = + 和旁轴轨迹方程(高斯轨迹方程)对比: ( ( ) ) ( ) ( ( ) ) ( ( ) ) ( ( ) )( ( ( ) ) ) 0 0 0 0 2 1 2 2 2 1 0 2 1 0 4 z z z z z z z z e v V z m v mv r eV r e e V z m V z r eV r m m V z V z r V r = + = − + + + = + + + =

高斯轨迹方程 W(W'+4v,=0 近轴轨迹方程 VV+E.(VVFer')'+IV'r=0 上式即所谓“近轴轨迹方程”.它未采用0,≈v的旁轴假设.但 方程中亦未明显出现的高阶量.在某种意义上,它用初态动能的 不同代替了x'的差异.e.因电子而异,但对每个电子而言是不变 的,所以在同一物点发出、ε相同的电子群看来,此方程仍是“高斯 方程一般形式”的一种.如假定阴极电位不是0,而是“初始纵向动 能对应电位”ε,其形式与高斯方程无异.但其物理意义与根据旁 轴条件推出的高斯方程不同.后者认为电子的初始总动能皆为0, 故总动量P与电位V有确定的关系,而上式中的V充其量只能确 定纵向动量.从成像角度言之,旁轴方程认为初始总动能与理想粒 子一致的粒子应准确成像(高斯像),总动能不一致者产生色差,初 速度方向不一致者产生球差:近轴方程则认为初始纵向动能一致 者可准确成像(称为“近轴高斯像”),不一致者产生“色球差”,常不 再区分纵向动能的不一致是因为总动能不同还是速度方向不同
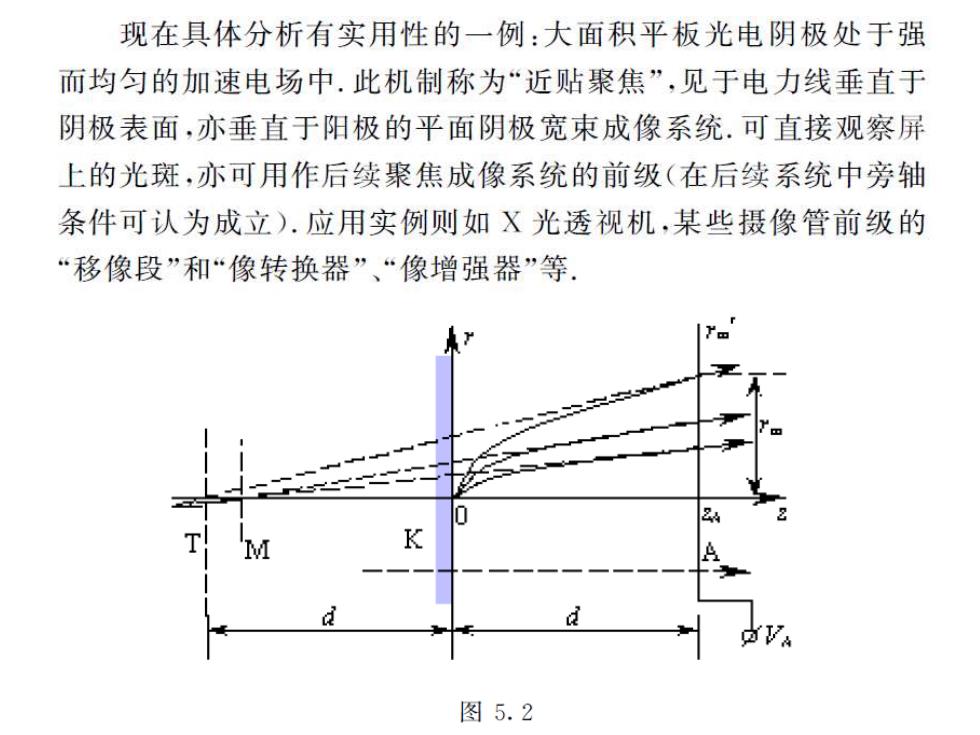
现在具体分析有实用性的一例:大面积平板光电阴极处于强 而均匀的加速电场中.此机制称为“近贴聚焦”,见于电力线垂直于 阴极表面,亦垂直于阳极的平面阴极宽束成像系统.可直接观察屏 上的光斑,亦可用作后续聚焦成像系统的前级(在后续系统中旁轴 条件可认为成立).应用实例则如X光透视机,某些摄像管前级的 “移像段”和“像转换器”、“像增强器”等. 2 d VA 图5.2

(v(=)+6.)(V()+6.))+ivr-0 V"=0 (T()+=0→T)+'=C ()-0.)C i.V(=)+6.)r'=E ve- 晋* 八d1 过物点的轨迹在x=0时=0,故 代入位场表达式即得
( ( ) )( ( ( ) ) ) ( ( ( ) ) ) ( ( ) ) ( ) ( ) ( ( ) ) ( ( ) ) ( ) 0 0 0 0 0 0 0 0 1 0 4 0 0 0 0 0 1 d 1 1 2 2 d d z z z z r r z r z z z r z r z A z z z A A r r r z r z z A A A A z z V z V z r V r V V z r V z r C v v V r C v v V z r r z V z V V z z d d d V V r z z z z V V V d V d z z d d + + + = = + = + = = = + = = + = = = = + = + − + + = , =