
问题4: 具有负值权的回路对于单源 最短通路问题的解有什么影 响?非负值权的回路呢?

问题5: 在本章中介绍的算法基本思路 是一样的,那是什么? Bellman-Ford算法、DAG算法、Dijkstra算法 松弛+有序的松弛
Bellman-Ford算法、DAG算法、Dijkstra算法 松弛+有序的松弛

问题6: Relax到底在干什么? 为什么它会是最短路算法的核心?

Lemma 24.10(Triangle inequality) Let G =(V,E)be a weighted,directed graph with weight function w:E-R and source vertex s.Then,for all edges (u,v)EE,we have 8(s,v)≤6(s,W+w(u,v) 这是最短的路 这是某条路径 的权重 的权重而已
这是最短的路 的权重 这是某条路径 的权重而已
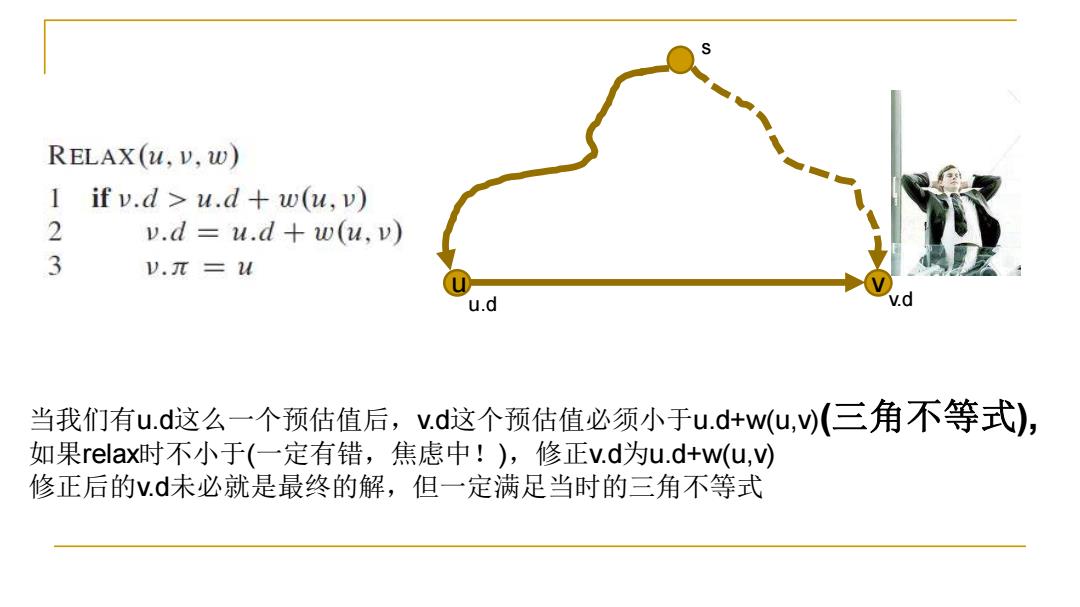
RELAX(u,v,w) 1 if v.d u.d+w(u,v) 2 v.d u.d+w(u,v) 3 V.π=u u.d 当我们有u.d这么一个预估值后,v.d这个预估值必须小于u.d+wu,v)(三角不等式), 如果relaxl时不小于(一定有错,焦虑中!),修正v.d为u.d+w(u,) 修正后的V.d未必就是最终的解,但一定满足当时的三角不等式
s u v 当我们有u.d这么一个预估值后,v.d这个预估值必须小于u.d+w(u,v)(三角不等式), 如果relax时不小于(一定有错,焦虑中!),修正v.d为u.d+w(u,v) 修正后的v.d未必就是最终的解,但一定满足当时的三角不等式 u.d v.d