
超声治疗学—Chap.6重广医科大学三、声场中空化泡的运动气泡动力学理论提供描述液体中半径R.的单个气泡在声场作用下行为的O运动方程,即著名的Rayleigh-Plesset方程,其形式如下:3Yd’R.3dRR.2g 4n dRORP sino t+P,-Pdt?R2dtRRdtdR和和些分别是泡壁径向运动的振动速度式中,R是气泡某时刻的半径;和加速度;P和n分别是液体的密度和粘滞系数;是泡内气体的比热容比;P代表声压幅值;w=2πf代表声波的角频率,其中是声波频率;P=2+P-P代表静态时泡内气体压强,其中为气泡半径为R时的表面张力,是表面张力系数,P.为液体中静压强,P为泡内蒸气压
超声治疗学——Chap.6 三、声场中空化泡的运动 ◇气泡动力学理论提供描述液体中半径R0的单个气泡在声场作用下行为的 运动方程,即著名的Rayleigh-Plesset方程,其形式如下: 式中,R是气泡某时刻的半径; 和 分别是泡壁径向运动的振动速度 和加速度; 和 分别是液体的密度和粘滞系数;γ是泡内气体的比热 容比;PA代表声压幅值;ω =2 π f 代表声波的角频率,其中f是声波频 率; Pio= + P0 - Pv代表静态时泡内气体压强,其中 为气泡半径为R0 时的表面张力, 是表面张力系数,P0为液体中静压强,Pv为泡内蒸气 压。 2 3 2 0 2 d 3 d 2 4d sin d 2d d A RR R R R P PP P R RR ϒ σ ρ ρ ⎛ ⎞ ⎛ ⎞ + = +−− − − ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ η i0 v 0 ωt tt t d d R t 2 2 d d R t ρ η 0 2 R σ 0 2 R σ σ

超声治疗学Chap.6重广醫科大学UNIV三、声场中空化泡的运动若对此方程作一定线性近似,即假定液体无粘滞性,即Ⅱ=0;气泡半径变化较小,即R=R。+r,且r<Ro。则可推导出此情况下,气泡的半径变量随时间的变化关系:PAasino t+sinwrtpRo(r-0Wr式中的,是在推导过程中确定的气泡共振角频率。由W,=2πf关系式,则可得到半径为R.的气泡共振频率为:112g2031f.R.R.2元RP
超声治疗学——Chap.6 三、声场中空化泡的运动 ◇若对此方程作一定线性近似,即假定液体无粘滞性,即 = 0;气 泡半径变化较小,即R= R0 + r,且r < R0。则可推导出此情况下, 气泡的半径变量r随时间的变化关系: r = 式中的ωr是在推导过程中确定的气泡共振角频率。由ωr = 2 πfr 关系式,则可得到半径为R0的气泡共振频率为: 0 0 00 11 2 2 3 2 f P R R R σ σ π ρ⎡ ⎛ ⎞ ⎤ = +− ⎢ ⎜ ⎟ ⎥ ⎣ ⎝ ⎠ ⎦ r γ η ( ) A 0 2 2 sin sin P R ⎛ ⎞ ⎜ ⎟ ⎝ ⎠ r ρ r r + – ω ωt ω t ω ω ω Pa PA

超声治疗学一-Chap.6重广医科大学UNIVER、声场中空化泡的运动由于一般情况下,单原子气体,多数双原子气体或空气,Y>1,故C20< 3P+常有R故此式可近似为:R20R.2元R与此频率相对应的气泡半径Rr称为共振半径,故可把上式改写为下面形式:3y2gR~2元f.VR,0若水中气泡半径R=0.1mm,则算出其共振频率f~33kHz
超声治疗学——Chap.6 三、声场中空化泡的运动 ◇由于一般情况下,单原子气体,多数双原子气体或空气, >1,故 常有 3 ,故此式可近似为: 与此频率相对应的气泡半径 称为共振半径,故可把上式改写为 下面形式: Î 若水中气泡半径R0 = 0.1mm,则算出其共振频率fr≈ 33 kHz。 γ 0 2 R σ ≪ γ 0 0 2 P R ⎛ ⎞ σ ⎜ ⎟ + ⎝ ⎠ 0 0 0 13 2 2 f P R Rσ π ρ⎛ ⎞ ≈ + ⎜ ⎟ ⎝ ⎠ r γ Rr 0 0 13 2 2 R P f R σ π ρ ⎛ ⎞ ≈ + ⎜ ⎟ ⎝ ⎠ r r γ
-Chap.6超声治疗学一重广医科大学ICALUNIVERS四、稳态空化与瞬态空化稳态空化(Steadycavitation/non-inertialcavitation)-P130)瞬态空化(Transientcavitation/inertialcavitation)TRANSIENTCAVITATION:THEORIGINOFSONOCHEMISTRYsoundpressureAAAAAAAAAAAcompressionwavesMPLOSIONSHOCKWAVEchanges in·米0..0..bubblesizeHOTRAPIFORMATIONSPOTQUENCHINGtimet500a400200Time(usec)
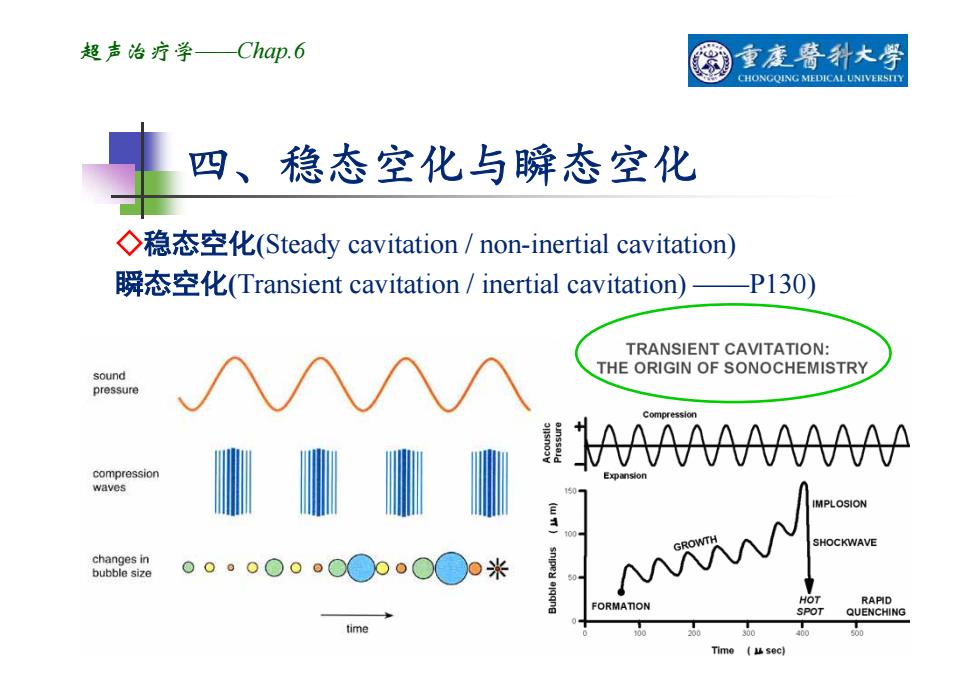
超声治疗学——Chap.6 四、稳态空化与瞬态空化 ◇稳态空化(Steady cavitation / non-inertial cavitation) 瞬态空化(Transient cavitation / inertial cavitation) ——P130)

超声治疗学—Chap.6重广医科大学四、稳态空化与瞬态空化瞬态空化一当用强度较高的超声波辐照液体时,声场中气泡的动力学过程变得更为复杂和激烈。在声波的负压半周期内空化核(微小气泡)迅速膨胀,随后又在声波正半周期内气泡被压缩以至崩溃。利用气泡动力学方程6-5。1.气泡崩溃时达到的泡壁最大压缩速度27P(y-)RU.max3proY式中:P=Pa+Pa~P。为气泡的外界压强;Q为气泡半径为R时泡内的压强(气压、蒸汽压与表面张力的总压力)
超声治疗学——Chap.6 四、稳态空化与瞬态空化 瞬态空化——当用强度较高的超声波辐照液体时,声场中气泡 的动力学过程变得更为复杂和激烈。在声波的负压半周期内空 化核(微小气泡)迅速膨胀,随后又在声波正半周期内气泡被 压缩以至崩溃。 Î 利用气泡动力学方程6-5。 1. 气泡崩溃时达到的泡壁最大压缩速度 式中:P = P0+ PA≈P0 为气泡的外界压强;Q为气泡半径为R0时 泡内的压强(气压、蒸汽压与表面张力的总压力)。 ( ) ( ) 1 1 max 2 1 1 3 P P U ρ Q − − − ⎡ ⎤ ≈ ⎢ ⎥ ⎣ ⎦ γ γ γ γ γ