
广义的表面自由能定义:(上式) r=(OU 比表面内能 y=(%A小sn 比表面焓 y=( 比表面Helmholtz函数 比表面能 y=( 比表面Gibbs函数 ¥:单位表面积表面层的分子比体系内部同样数量的分子所高出的能量值。 保持相应的特征变量不变,每增加单位表面积时,相应热力学函数的增值。 狭义的表面自由能定义 &G 单位:J·m2 保持温度、压力和组成不变,每增加单位表面积时,Gbbs自由能的增加值称为 表面Gibbs自由能,或简称表面自由能或表面能,用符号o或y表示。 四、表(界)面张力{surface(interface)tension} 1.概念 将一含有一个活动边框的金属线框架放在肥皂液中,然后取出悬挂,活动边在下面。 F(W+W,)8 =2y1 由于金属框上的肥皂膜的表面张力作用,可滑动的边会被向上拉,直至顶部。 如果在活动边框上挂一重物,使重物质量2与边框质量M所产生的重力F与总的 表面张力大小相等方向相反,则金属丝不再滑动。 这时 F=2yl L是滑动边的长度,'因膜有两个面,所以边界总长度为2L,就是作用于单位边界 上的表面张力。 在两相(特别是气-液)界面上,处处存在着一种张力,这种力垂直与表面的边界,指 向液体方向并与表面相切。 把作用于单位边界线上的这种力称为表面张力,用¥或σ表示。 表面张力的单位是:N·m。 在金属线框中间系一线圈,一起浸入肥皂液中,然后取出,上面形成一液膜。由于 以线圈为边界的两边表面张力大小相等方向相反,故线圈成任意形状可在液膜上移动。 若刺破线圈中央的液膜,线圈内侧张力消失,外侧表面张力立即将线圈绷成一个圆形
广义的表面自由能定义:(上式) )( )( )( )( ,, ,, ,, ,, npT nVT npS nVS A G A A H A U ∂ = ∂ ∂ = Α∂ ∂ = ∂ ∂ = ∂ γ γ γ γ 比表面内能 比表面Gibbs函数 比表面Helmholtz函数 比表面焓 比表面能 γ:单位表面积表面层的分子比体系内部同样数量的分子所高出的能量值。 保持相应的特征变量不变,每增加单位表面积时,相应热力学函数的增值。 狭义的表面自由能定义 单位: J·m-2 保持温度、压力和组成不变,每增加单位表面积时,Gibbs 自由能的增加值称为 表面 Gibbs 自由能,或简称表面自由能或表面能,用符号 σ 或γ表示。 四、表(界)面张力{surface (interface) tension} 1.概念 将一含有一个活动边框的金属线框架放在肥皂液中,然后取出悬挂,活动边在下面。 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l 2 γ l W 2 2 γ l W 2 2 γ l W 2 2 γ l W 2 2 γ l W 2 2 γ l W 2 2 γ l W 2 2 γ l W 2 2 γ l W 2 2 γ l W 2 2 γ l W 2 2 γ l W 2 W 2 W 1 2 γ l = ( 1 2 F W Wg + ) = 2 γ l = ( 1 2 F W Wg + ) = 由于金属框上的肥皂膜的表面张力作用,可滑动的边会被向上拉,直至顶部。 如果在活动边框上挂一重物,使重物质量 W2 与边框质量 W1 所产生的重力 F 与总的 表面张力大小相等方向相反,则金属丝不再滑动。 这时 L 是滑动边的长度,因膜有两个面,所以边界总长度为 2L, 就是作用于单位边界 上的表面张力。 B , , ( )pT n G A γ ∂ = ∂ F =2γl 在两相(特别是气-液)界面上,处处存在着一种张力,这种力垂直与表面的边界,指 向液体方向并与表面相切。 把作用于单位边界线上的这种力称为表面张力,用 γ 或 σ 表示。 表面张力的单位是:N·m-1 。 在金属线框中间系一线圈,一起浸入肥皂液中,然后取出,上面形成一液膜。由于 以线圈为边界的两边表面张力大小相等方向相反,故线圈成任意形状可在液膜上移动。 若刺破线圈中央的液膜,线圈内侧张力消失,外侧表面张力立即将线圈绷成一个圆形

如图,清楚的显示出表面张力的存在。 表(界)面张力是平行于表面且垂直作用于表面上单位长度线段上的表面紧缩力。 (比)表面Gibbs函数和表面张力在数值上是相等的 2.影响表面张力的因素 (1)分子间相互作用力的影响 对纯液体或纯固体,表面张力决定于分子间形成的化学键能的大小,一般化学键越 强,表面张力越大。固体比液体大 八金属键)>Y(离子键)>Y(极性共价键)》>《非极性共价键) 两种液体间的界面张力,界于两种液体表面张力之间。 (2)温度的影响 对绝大多数液体 温度升高,表面张力下降。T↑,Y。 Ramsay和Shields提出的y与T的经验式较常用: R-S方程 y=kWm为(T-T-6.0) Ym23=k(1c-T-6.0) 式中T。:临界温度 V。:液体的摩尔体积 k:经验参数,对非缔合的非极性液体k≈2.2×10JK Guggenheim方程 y=1-” 式中¥。,n:经验参数,对有机液体,n=11/9,对金属,n≈1 但对Cd,Fe,Cu合金及一些硅酸盐液体,T↑Y↑。 (3)压力的影响 表面张力一般随压力的增加而下降。因为压力增加,气相密度增加,表面分子受 力不均匀性略有好转。另外,若是气相中有别的物质,则压力增加,促使表面吸附增 加,气体溶解度增加,也使表面张力下降。 具有巨大比表面的体系具有巨大的表面能,是热力学不稳定体系, 例如:将1g水分割成半径为1nm的小水滴,表面积为3000m,表面能为220J. 任何体系都有降低表面能的趋势
如图,清楚的显示出表面张力的存在。 表(界)面张力是平行于表面且垂直作用于表面上单位长度线段上的表面紧缩力。 (比)表面 Gibbs 函数和表面张力在数值上是相等的 2.影响表面张力的因素 (1)分子间相互作用力的影响 对纯液体或纯固体,表面张力决定于分子间形成的化学键能的大小,一般化学键越 强,表面张力越大。固体比液体大 γ(金属键)> ( )> ( γ 离子键)> ( )> ( γ 极性共价键)> ( γ 非极性共价键) 两种液体间的界面张力,界于两种液体表面张力之间。 (2)温度的影响 对绝大多数液体 温度升高,表面张力下降。 T↑,γ↓。 Ramsay 和 Shields 提出的γ与 T 的经验式较常用: R-S 方程 γVm2/3 =k(Tc-T-6.0) 6( )0. 3 = −− − γ TkV 2 Tcm 式中Tc :临界温度 Vm :液体的摩尔体积 k:经验参数,对非缔合的非极性液体 k≈2.2×10-7 J K-1 )1( 0 n Tc T γγ −= Guggenheim 方程 式中γ0 ,n : 经验参数,对有机液体,n=11/9,对金属 , n≈1 但对 Cd, Fe, Cu 合金及一些硅酸盐液体,T↑γ↑。 (3)压力的影响 表面张力一般随压力的增加而下降。因为压力增加,气相密度增加,表面分子受 力不均匀性略有好转。另外,若是气相中有别的物质,则压力增加,促使表面吸附增 加,气体溶解度增加,也使表面张力下降。 具有巨大比表面的体系具有巨大的表面能,是热力学不稳定体系, 例如:将 1 g水分割成半径为 1 nm的小水滴,表面积为 3000m2 , 表面能为 220 J. 任何体系都有降低表面能的趋势

第二节 弯曲表面下的附加压力与蒸气压 一.弯曲液面下的附加压力 〔1.在平面上 弯曲表面下的附加压力 2.在凸面上 3.在凹面上 1.在平面上 研究以AB为直径的一个环作为边界,由于环上每点的两边都存在表面张力,大小相 等,方向相反,所以没有附加压力。 设向下的大气压力为,向上的反作用力也为,附加压力,等于零。 P=P6-P=0 液面正面图 (2)在凸面上: 研究以AB为弦长的一个球面上的环作为边界。由于环上每点两边的表面张力都与 液面相切,大小相等,但不在同一平面上,所以会产生一个向下的合力。 所有的点产生的合力和为乃,称为附加压力。凸面上受的总压力为:+乃 A为大气压力,为附加压力。 剖 g 图 Ps 附加压力示意图 (3)在凹面上: 研究以AB为弦长的一个球形凹面上的环作为边界。由于环上每点两边的表面张力 都与凹形的液面相切,大小相等,但不在同一平面上,所以会产生一个向上的合力。 所有的点产生的合力和为n,称为附加压力。凹面上向下的总压力为:。乃, 所以凹面上所受的压力比平面上小。 PS 剖 图 水 附加压力示意图
第二节 弯曲表面下的附加压力与蒸气压 一. 弯曲液面下的附加压力 弯曲表面下的附加压力 1.在平面上 2.在凸面上 3.在凹面上 弯曲表面下的附加压力 1.在平面上 2.在凸面上 3.在凹面上 1.在平面上 研究以 AB 为直径的一个环作为边界,由于环上每点的两边都存在表面张力,大小相 等,方向相反,所以没有附加压力。 设向下的大气压力为po,向上的反作用力也为po ,附加压力ps等于零。 液面正面图 ppp s 00 = − = 0 (2)在凸面上: 研究以 AB 为弦长的一个球面上的环作为边界。由于环上每点两边的表面张力都与 液面相切,大小相等,但不在同一平面上,所以会产生一个向下的合力。 所有的点产生的合力和为 ps ,称为附加压力。凸面上受的总压力为:po+ ps po为大气压力, ps为附加压力。 剖 面 图 附加压力示意图 (3)在凹面上: 研究以 AB 为弦长的一个球形凹面上的环作为边界。由于环上每点两边的表面张力 都与凹形的液面相切,大小相等,但不在同一平面上,所以会产生一个向上的合力。 所有的点产生的合力和为ps ,称为附加压力。凹面上向下的总压力为:po- ps , 所以凹面上所受的压力比平面上小。 剖 面 图 附加压力示意图
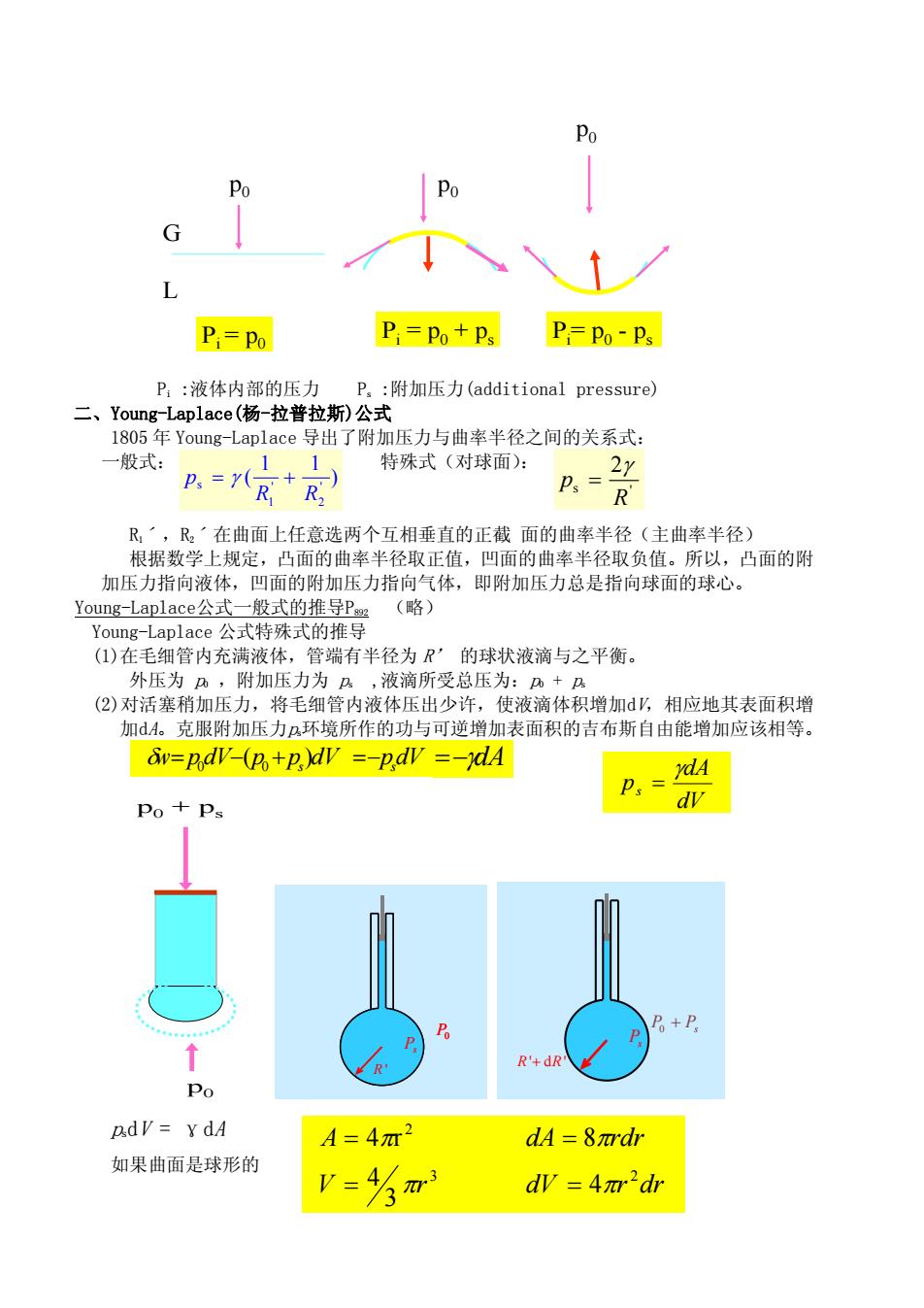
Po Po Pi=Po Pi=Po+Ps P=Po-Ps P::液体内部的压力 P。:附加压力(additional pressure) 二、Young-Laplace(杨-拉普拉斯)公式 l805年Young-Laplace导出了附加压力与曲率半径之间的关系式: 一般式: 1 1 特殊式(对球面): Ps=Y( 2y R、 Ps= R R′,R2’在曲面上任意选两个互相垂直的正截面的曲率半径(主曲率半径) 根据数学上规定,凸面的曲率半径取正值,凹面的曲率半径取负值。所以,凸面的附 加压力指向液体,凹面的附加压力指向气体,即附加压力总是指向球面的球心。 Young--Laplace公式一般式的推导Pg(略) Young-Laplace公式特殊式的推导 (1)在毛细管内充满液体,管端有半径为R'的球状液滴与之平衡。 外压为,附加压力为,液滴所受总压为:+及 (2)对活塞稍加压力,将毛细管内液体压出少许,使液滴体积增加少,相应地其表面积增 加A。克服附加压力环境所作的功与可逆增加表面积的吉布斯自由能增加应该相等。 v=pdv-(po+pdv =-pdv =-dA ydA P Po Ps P Po+P: R'+dR' Po pdv=YdA A=4m2 dA =8nrdr 如果曲面是球形的 3 dW=4π2dr
p0 G L Pi = p0 p0 ps Pi = p0 + ps ps p0 Pi = p0 - ps Pi :液体内部的压力 Ps :附加压力(additional pressure) 二、Young-Laplace(杨-拉普拉斯)公式 1805 年 Young-Laplace 导出了附加压力与曲率半径之间的关系式: s ' 2 p R γ = 一般式: 特殊式(对球面): s ' ' 1 2 1 1 p ( ) R R = + γ R1ˊ,R2ˊ在曲面上任意选两个互相垂直的正截 面的曲率半径(主曲率半径) 根据数学上规定,凸面的曲率半径取正值,凹面的曲率半径取负值。所以,凸面的附 加压力指向液体,凹面的附加压力指向气体,即附加压力总是指向球面的球心。 Young-Laplace公式一般式的推导P892 (略) Young-Laplace 公式特殊式的推导 (1)在毛细管内充满液体,管端有半径为 R’ 的球状液滴与之平衡。 外压为 p0 ,附加压力为 ps ,液滴所受总压为:p0 + ps (2)对活塞稍加压力,将毛细管内液体压出少许,使液滴体积增加dV,相应地其表面积增 加dA。克服附加压力ps环境所作的功与可逆增加表面积的吉布斯自由能增加应该相等。 )( δ 0 −= 0 + s dVppdVpw dVp −= s =−γdA dV dA ps γ = p0 + ps p0 R ' Ps P0 R ' Ps P0 R ' Ps P0 Ps P0 + Ps R R 'd' + Ps P0 + Ps R R 'd' + psdV = γdA 4 3 4 8 r4 3 2 2 rV drrdV A rdrdA π π π π = = = = 如果曲面是球形的

代入得: 2y Ps= R' 讨论: l.凸形液面(convex)(r>0) ps>0,p:>p。; 凹形液面(concave)(r<0) ps<0,p<p。: 平面 r=∞ps=0,p=p0 Ps总是指向曲面的球心 2.y越大,r越小,则p越大 3.由于液体或固体小颗粒的内部存在较大的附加压力,使组分的化学势发生变化,引 起体系物理、化学性质的改变。 4.对于液泡(pao)来说(如肥皂泡),因有内外有两个表面,所以平衡时液泡内部气体比 液泡外部气体的压力大,其压力差△p。=4y/R。 解释1自由液滴或气泡(在不受外力场影响下),通常都呈球形。 一方面:由于在相同体积前提下,球形的表面积最小,表面张力就小,稳定。 另方面:当液滴出现不规则弯曲表面时,在液面的不同部位,由于弯曲方向和弯曲半 径都不一样,产生的附加压力大小和方向也就不同,这种不平衡力迫使液滴 自动调整成球形。因为只有球形才能使球面上各点曲率半径相同,附加压力 相等,方向都指向中心,这样的液滴才能稳定存在。 但由于重力场的影响,通常液滴呈椭扁球形体,这时附加压力符合杨-拉普拉斯)公式。 解释2毛细管现象:液体在毛细管中形成凹液面时,液体会在毛细管中上升,而在管中 形成凸液面时会下降。 毛细管插入水中时,管中的水柱表面呈凹形曲面,结果使水柱上升到一定高度。 三、附加压力与毛细管中液面高度的关系 R 1.曲率半径R与毛细管半径R的关系: R=- 如果曲面为球面,则R=R。 cos0 =(PI-Ps)gh 2.P,= 因p>》Pg P:= 2Y =pigh R 2ycose 一般式:P,= =△pgh R
' 2 s R p γ 代入得: = 讨论: 1. 凸形液面(convex) (r>0) ps >0 , pi >po ; 凹形液面 (concave) (r <0) ps < 0 , pi <po ; 平面 r = ∞ ps = 0 , pi = po Ps 总是指向曲面的球心 2. γ越大,r越小,则 ps 越大 3. 由于液体或固体小颗粒的内部存在较大的附加压力,使组分的化学势发生变化,引 起体系物理、化学性质的改变。 4.对于液泡(pao)来说 (如肥皂泡),因有内外有两个表面,所以平衡时液泡内部气体比 液泡外部气体的压力大,其压力差Δps = 4γ/R。 解释 1 自由液滴或气泡(在不受外力场影响下),通常都呈球形。 一方面:由于在相同体积前提下,球形的表面积最小,表面张力就小,稳定。 另方面:当液滴出现不规则弯曲表面时,在液面的不同部位,由于弯曲方向和弯曲半 径都不一样,产生的附加压力大小和方向也就不同,这种不平衡力迫使液滴 自动调整成球形。因为只有球形才能使球面上各点曲率半径相同,附加压力 相等,方向都指向中心,这样的液滴才能稳定存在。 但由于重力场的影响,通常液滴呈椭扁球形体,这时附加压力符合杨-拉普拉斯)公式。 解释 2 毛细管现象:液体在毛细管中形成凹液面时,液体会在毛细管中上升,而在管中 形成凸液面时会下降。 毛细管插入水中时,管中的水柱表面呈凹形曲面,结果使水柱上升到一定高度。 三、附加压力与毛细管中液面高度的关系 cos R R θ =´ 1.曲率半径 R'与毛细管半径 R 的关系: 如果曲面为球面,则 R'=R。 2 ( ) s l g p gh R γ ==− ρ ρ ´ 2. 2 ( ) s l g γ p gh R ==− ρ ρ ´ 因ρl >>ρg 2 s l p gh R γ = = ρ ´ 2 cos ps gh R γ θ = =Δρ 一般式: