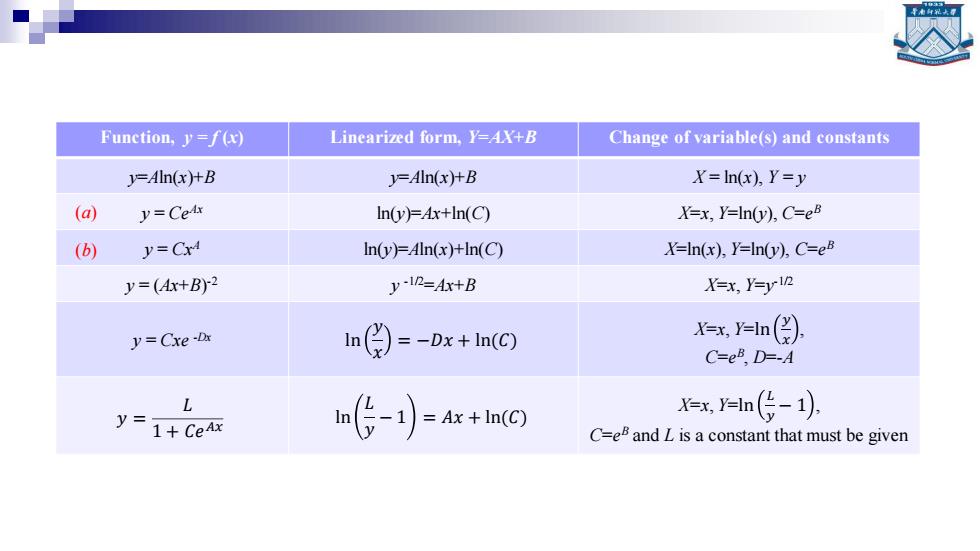
Function,y=f(x) Linearized form,Y=AX+B Change of variable(s)and constants y=Aln(x)+B y=Aln(x)+B Y=In(x),Y=y (a y=CeAx In(y)=Ax+In(C) X=x,Y=In(y),C=e (b) y=Cx4 In(y)=4ln(x)+In(C) X=In(x),Y=In(y),C=e y=(Ax+B)2 y-IR=Ax+B X=x,Y=yin y=Cxe-Dx n( =-Dx+In(C) Xx,=n(的) C=eR,D=-A L y=1+CeAx In-1)=4x+In(C) x,n(货-1), C=e and L is a constant that must be given
Function, y = f (x) Linearized form, Y=AX+B Change of variable(s) and constants y=Aln(x)+B y=Aln(x)+B X = ln(x), Y = y y = CeAx ln(y)=Ax+ln(C) X=x, Y=ln(y), C=e B y = CxA ln(y)=Aln(x)+ln(C) X=ln(x), Y=ln(y), C=e B y = (Ax+B) -2 y -1/2=Ax+B X=x, Y=y -1/2 y = Cxe -Dx ln 𝑦 𝑥 = −𝐷𝑥 + ln(𝐶) X=x, Y=ln 𝑦 𝑥 , C=e B , D=-A 𝑦 = 𝐿 1 + 𝐶𝑒𝐴𝑥 ln 𝐿 𝑦 − 1 = 𝐴𝑥 + ln(𝐶) X=x, Y=ln 𝐿 𝑦 − 1 , C=e B and L is a constant that must be given (a) (b)
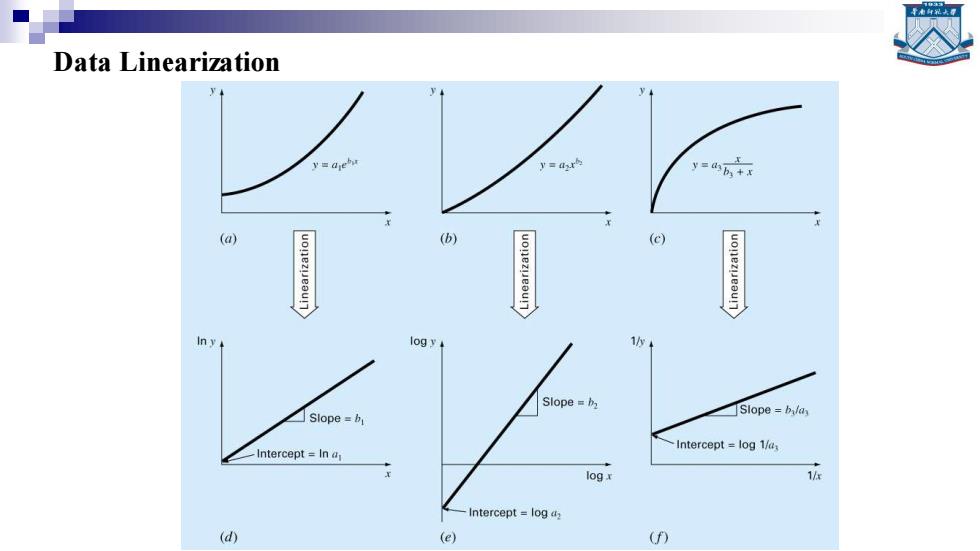
Data Linearization y=4.r y=db+x (a) (b) (c) log y 1y+ Slope=h Slope =b Slope =blay Intercept log 1/ Intercept In a log 1/ Intercept log a: (d) (e) (D
Data Linearization

Linear Least squares Suppose that N data points {(k)}and a set of Mlinear independent functions f(x)}are given.We want to find Mcoefficients {c}so that the function fx)given by the linear combination f-之cj国 will minimize the sum of the squares of the errors: G-2-2[位a小】
Linear Least Squares ◼ Suppose that N data points {(xk ,yk )} and a set of M linear independent functions {f j (x)} are given. We want to find M coefficients {cj} so that the function f(x) given by the linear combination will minimize the sum of the squares of the errors: 1 ( ) ( ) M j j j f x c f x = = 2 2 1 2 1 1 1 ( , ,..., ) ( ( ) ) ( ) N N M M k k j j k k k k j E c c c f x y c f x y = = = = − = −

For E to be minimized it is necessary that each partial derivative be zero(i.e.,OE/oc,=0,for i=1,2,...,M),and this results in the system of equations [2》-0 fori1,2,…,M Interchanging the order of the summations in the equations aboved will produce an MX M system of linear equations where the unknown are the coefficients {c).They are called the normal equations: 22w,-2i0r=12M (4.40)
◼ For E to be minimized it is necessary that each partial derivative be zero(i.e., ), and this results in the system of equations ◼ Interchanging the order of the summations in the equations aboved will produce an M×M system of linear equations where the unknown are the coefficients {cj}. They are called the normal equations: / 0, for 1,2, , E c i M i = = 1 1 ( ) ( ( )) 0 N M j j k k i k k j c f x y f x = = − = for i=1,2,…,M. 1 1 1 ( ) ( ) ( ) M N N i k j k j i k k j k k f x f x c f x y = = = = for i=1,2,…,M. (4.40)

Matrix Formulation Construct the matrices F and F as follows: f(x)(x)…f(x) (x) f(x2) (x) … (xx) f(x2)(x2) …fM(x2) f5() … F= F'= f(x2) (x;) (xx) f(x;) f(x;) …fM(x3) fu (x)fu (x2)f (x;) fu (xx) f(xx)(xx) fu(x) ■ The element in the ith row and jth column of FF is the coefficient of c in the ith row in equation(4.40);that is, N >fi()fi(xk)=fi()f()+fi(xz)fj(x2)++fi(xN)fj(xN). k=1
Matrix Formulation ◼ Construct the matrices F and F’ as follows: ◼ The element in the ith row and jth column of F’F is the coefficient of cj in the ith row in equation (4.40); that is, 𝑘=1 𝑁 𝑓𝑖 (𝑥𝑘)𝑓𝑗 (𝑥𝑘) = 𝑓𝑖 𝑥1 𝑓𝑗 𝑥1 + 𝑓𝑖 𝑥2 𝑓𝑗 𝑥2 + ⋯ + 𝑓𝑖 𝑥𝑁 𝑓𝑗 𝑥𝑁 . 1 1 2 1 1 1 2 2 2 2 1 3 2 3 3 1 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) , ( ) ( ) ( ) M M M N N M N f x f x f x f x f x f x F f x f x f x f x f x f x = 1 1 1 2 1 3 1 2 1 2 2 2 3 2 1 2 3 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ' . ( ) ( ) ( ) ( ) N N M M M M N f x f x f x f x f x f x f x f x F f x f x f x f x =