哈尔滨工业大学：《信息检索》课程教学资源（课件讲义）信息检索模型 IRModel

向量空间模型 实际上，这些词项是相互关联的 ·当你在一个文档中看到“计算机”，非常有可 能同时看到“科学” ·当你在一个文档中看到“计算机”，有中等的 可能性同时看到“商务” ■当你在一个文档中看到“商务”，只有很少的 机会同时看到“科学

向量空间模型 „ 实际上，这些词项是相互关联的 „ 当你在一个文档中看到 “计算机 ” , 非常有可 能同时看到 “科学 ” „ 当你在一个文档中看到 “计算机 ” , 有中等的 可能性同时看到 “商务 ” „ 当你在一个文档中看到 “商务 ”，只有很少的 机会同时看到 “科学

向量空间模型 ■2个索引项构成一个二维空间，一个文档可能 包含0,1或2个索引项 ·d=〈0,0〉（一个索引项也不包含） ·d=(0,0.7〉（包含其中一个索引项） ·dk=〈1,2〉（包含两个索引项） 类似的，3个索引项构成一个三维空间，个索 引项构成n维空间 一个文档或查询式可以表示为个元素的线性 组合

向量空间模型 „ 2个索引项构成一个二维空间，一个文档可能 包含0, 1 或 2个索引项 „ di = 〈 0, 0 〉 (一个索引项也不包含 ) „ dj = 〈 0, 0.7 〉 (包含其中一个索引项 ) „ dk = 〈 1, 2 〉 (包含两个索引项 ) „ 类似的， 3个索引项构成一个三维空间， n个索 引项构成 n维空间 „ 一个文档或查询式可以表示为 n个元素的线性 组合

图示 举例： D1=2T1+3T2+5T3 D2=3T1+7T2+T 5 Q=0T1+0T2+2T3 D,=2T+3T2+5T Q=0T,+0T2+2T 23 T D2=3T1+7T2+T3 ·D比D2更接近Q吗？ 怎样衡量相似程度？夹角还是 投影

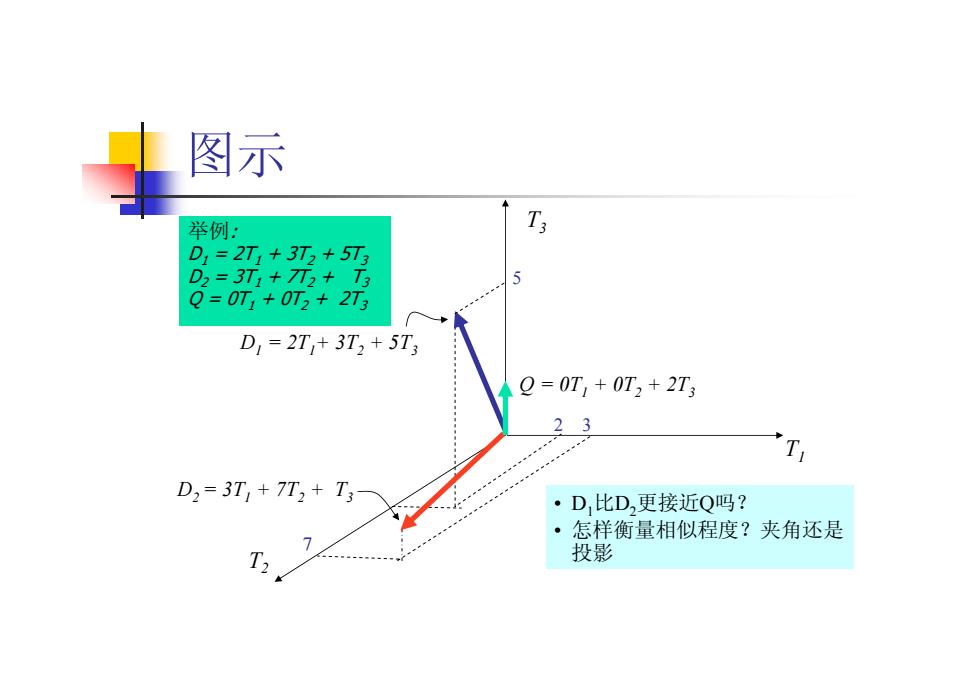
图示 举例: D1 = 2T1 + 3T2 + 5T3 D2 = 3T1 + 7T2 + T3 Q = 0T1 + 0T2 + 2T3 T3 T1 T2 D1 = 2T1+ 3T2 + 5T3 D2 = 3T1 + 7T2 + T3 Q = 0T1 + 0T2 + 2T3 7 2 3 5 • D1比D2更接近Q吗？ • 怎样衡量相似程度？夹角还是 投影

文档集一一般表示 向量空间中的N个文档可以用一个矩阵表示 ■矩阵中的一个元素对应于文档中一个词项的权 重。“0”意味着该词项在文档中没有意义，或该词 项不在文档中出现。 TT2 T D du dn D2 d21d22 da Dn dnl dn2 dnt

文档集 – 一般表示 „ 向量空间中的N个文档可以用一个矩阵表示 „ 矩阵中的一个元素对应于文档中一个词项的权 重。“0”意味着该词项在文档中没有意义，或该词 项不在文档中出现。 T1 T2 …. Tt D1 d11 d12 … d1t D2 d21 d22 … d2t : : : : : : : : Dn dn1 dn2 … dnt

相似度计算 相似度是一个函数，它给出两个向量之间的相似程度 ·查询式和文档都是向量，各类相似度存在于： 。两个文档之间 。两个查询式之间 ▣一个查询式和一个文档之间 ■人们曾提出大量的相似度计算方法，因为最佳的相似度计算 方法并不存在。 ■通过计算查询式和文档之间的相似度，可以： 。可以根据预定的重要程度对检索出来的文档进行排序 ·通过强制设定某个阈值，控制被检索出来的文档的数量 检索结果可以被用于相关反馈中，以便对原始的查询式进行 修正。（例如：将文档向量和查询式向量进行结合）

相似度计算 „ 相似度是一个函数，它给出两个向量之间的相似程度 „ 查询式和文档都是向量，各类相似度存在于： „ 两个文档之间 „ 两个查询式之间 „ 一个查询式和一个文档之间 „ 人们曾提出大量的相似度计算方法，因为最佳的相似度计算 方法并不存在。 „ 通过计算查询式和文档之间的相似度，可以： „ 可以根据预定的重要程度对检索出来的文档进行排序 „ 通过强制设定某个阈值，控制被检索出来的文档的数量 „ 检索结果可以被用于相关反馈中，以便对原始的查询式进行 修正。 (例如：将文档向量和查询式向量进行结合)