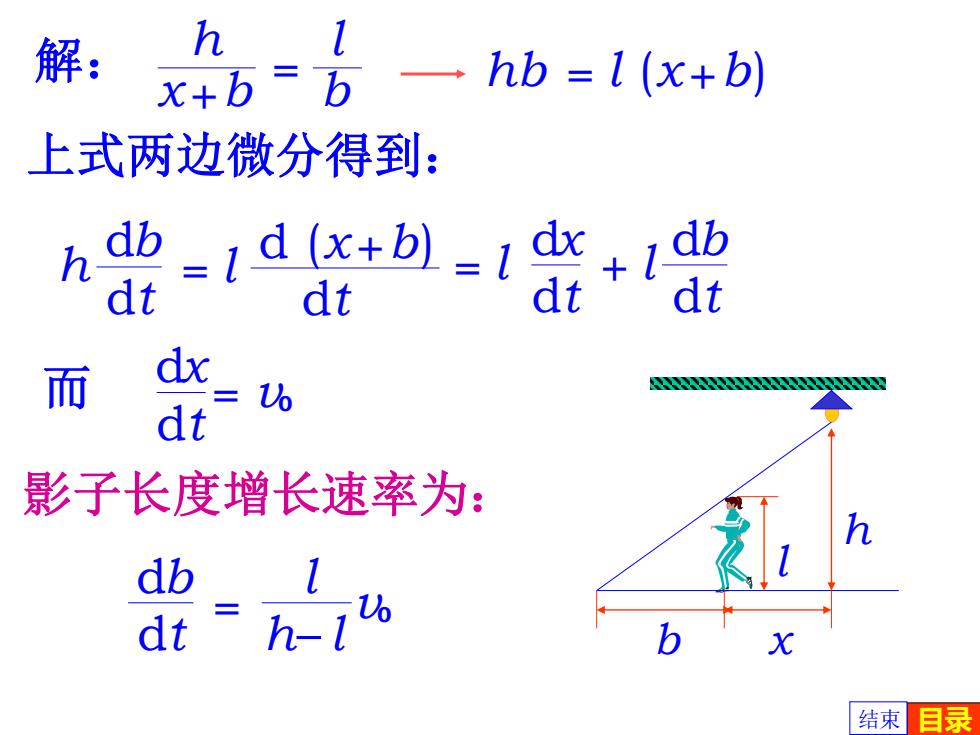
解: h xtb=b hb=1(x+b) 上式两边微分得到: db1d (x+b)=1dxd dt dt dt dt 而 dx = dt 影子长度增长速率为: db dt =1 -1 结束目录
h l b x x h +b l b 解: = d (x ) h +b = l dt db dt = db dt h l l v0 dx = l + dt db dt l 影子长度增长速率为: 目录 hb = l (x+b) 上式两边微分得到: dx = dt 而 v0 结束

hb=l(x+b) db dt h- 所以人影头顶移动速度为: d (x+b)_hdb h vo dt Idth-l 结束目录
= d (x+b) dt = h h l v0 h l db dt = db dt h l l v0 . . hb = l (x+b) 所以人影头顶移动速度为: 结束 目录
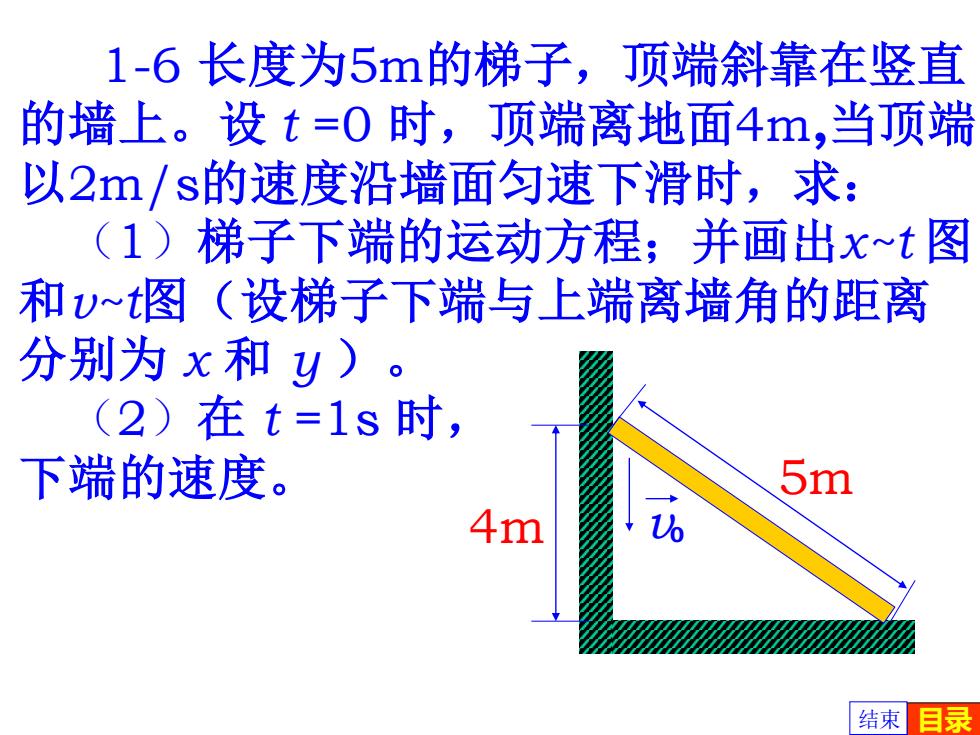
1-6长度为5m的梯子,顶端斜靠在竖直 的墙上。设t=0时,顶端离地面4m,当顶端 以2m/s的速度沿墙面匀速下滑时,求: (1)梯子下端的运动方程;并画出xt图 和v~t图(设梯子下端与上端离墙角的距离 分别为x和y)。 (2)在t=1s时, 下端的速度。 5m 4m 结束目录
1-6 长度为5m的梯子,顶端斜靠在竖直 的墙上。设 t =0 时,顶端离地面4m,当顶端 以2m/s的速度沿墙面匀速下滑时,求: (1)梯子下端的运动方程;并画出x~t 图 和v~t图(设梯子下端与上端离墙角的距离 分别为 x 和 y )。 (2)在 t =1s 时, 下端的速度。 5m 4m v0 结束 目录
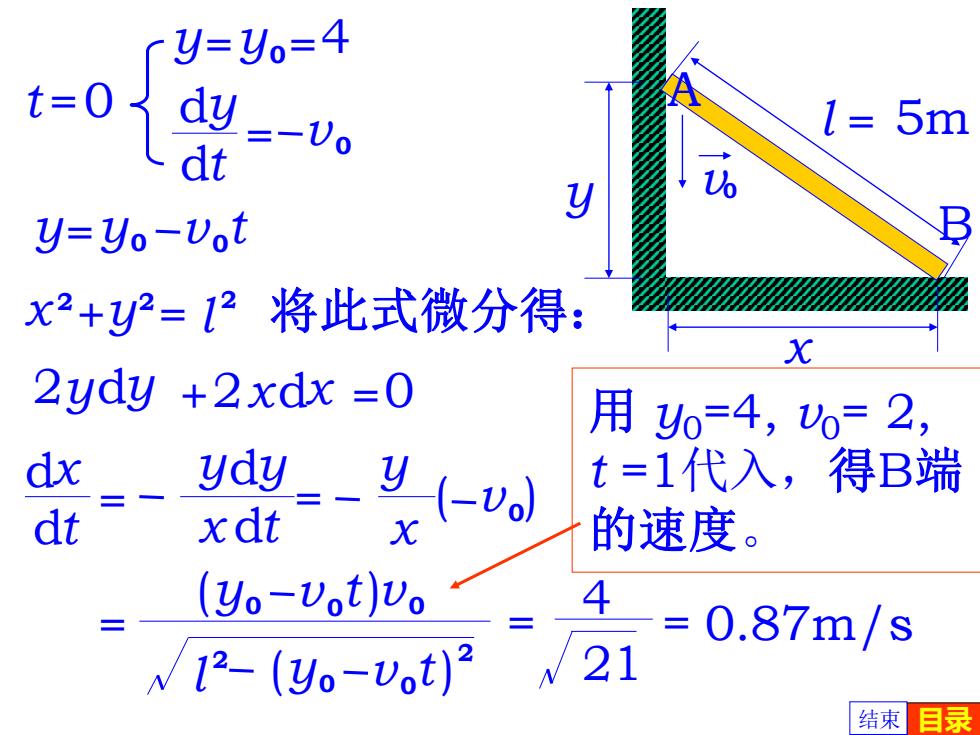
y=Yo=4 t=0 dy =-0 1=5m dt 10 y=yo-Vot x2+y=12将此式微分得: X 2ydy +2xdx =0 用y0=4,0=2, dx ydy y dt xdt -vo) t=1代入,得B端 X 的速度。 (yo-Vot)vo 4 0.87m/s N12-(yo-vot) 21 结束 录
t =0 x l 2 y = 2+ 2 y=y0 t v 0 2ydy +2xdx =0 0 t = y v 0 v 0 l 2 ( ) 2 y0 t v 0 ( ) = 4 21 = 0.87m/s 将此式微分得: y=y0=4 dt dy = v 0 目录 dx dt = dt dy x y x y = v 0 ( ) 5m v0 x y l = B A 用 y0=4, v0= 2, t =1代入,得B端 的速度。 结束
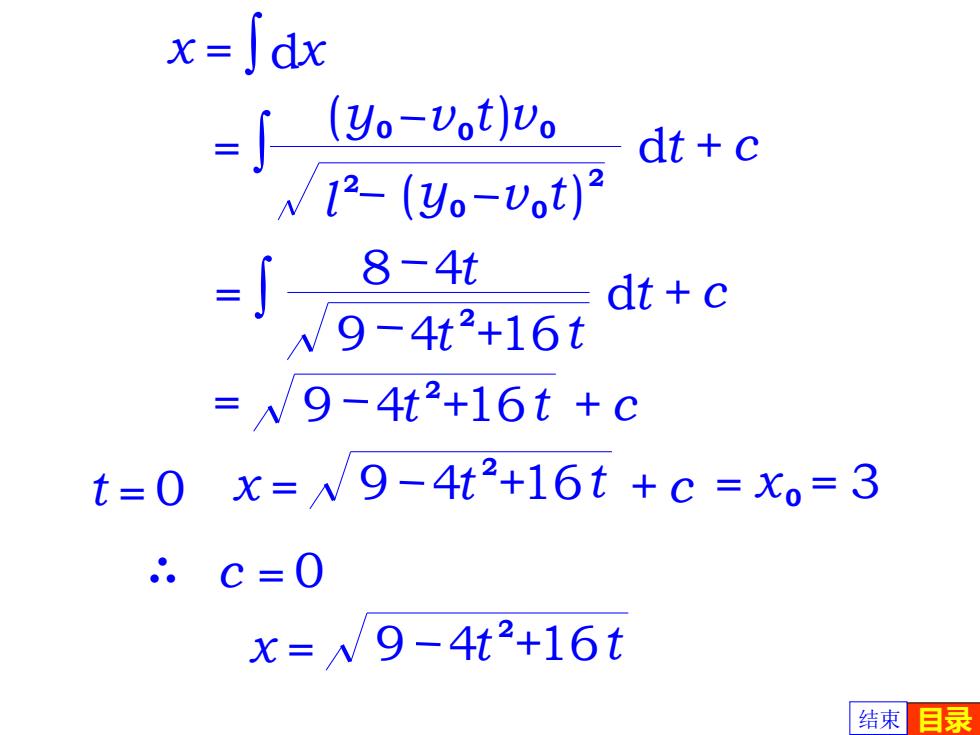
x=]dx =」-(-v]u。 dt c W12-(y0-vot)2 -g是416 8-4t dt c =/9-4t2+16t+c t=0x=W9-4t2+16t+c=x。=3 .c=0 x=xW9-4t2+16t 结束目录
y v dt 0 t = y v 0 0 + c l 2 ( ) 2 0 t v 0 ( ) 9 4 +16 2 t t 8 4t = dt +c 9 4 +16 2 = t t +c t = 0 x = dx x = 9 4 +16 2 t t +c = x 0 = 3 . c = 0 . x = 9 4 +16 2 t t 结束 目录