西安电子科技大学：《电动力学 Electrodynamics》课程教学资源（课件讲稿）第2章 静电场

Xidian University 静电场 二、唯一性定理 1.均匀单一介质 区域内p分布已知，{ 满足0=-P 若V边界上 、已知，或V边界上 9 已知，则V内场（静 电场)唯一确定。 证明： 假定泊松方程有两个解( 1≠92，有 E E oils p2ls pls 001 002 op 在边界上 On on S 令Φ=p1-p2 72Φ=720，-7202=0 西安电子科技大学

西安电子科技大学 二、唯一性定理 1．均匀单一介质 2       电场）唯一确定。   S  分布已知， 满足 若V边界上 已知，或V边界上 已知，则 V 内场（ 静 区域内 n S   证明： 1  2     1   2     2   2 假定泊松方程有两个解 ，有  S 1  2 S  S     S n 1    S n 在边界上  2 S n  令   1  2 0 2 2 1 2 2          静电场

Xidian University 静电场 中i。=01g-p2、=0 OΦ 001 002 =0 On On On 由格林第一公式 (v2Φ+VpV)dw=fvw.a 令Φ=0=W则 (Φv2Φ+(VD)2)dV=fDVΦ.as Φ、=0Φ7Φ·a5=0 72D=0→(VD)'ap=0 由于(VΦ)2≥0积分为零必然有 VΦ=0 ①=91-p2=常数 西安电子科技大学

西安电子科技大学    n S    S n 1 0 2    S n  由格林第一公式           V S dV dS  (  )   2 0   1  2  S S S   令     则          V S dV dS  ( ( ) ) 2 2 0 2        V ( ) dV 0 2   0 S     S dS 0   由于 ( ) 0 2   积分为零必然有   0   1  2 常数 静电场

静电场 Xidian University (1)若给定的是第一类边值关系Φ、=0 即常数为零。01=2电场唯一确定且 电势也是唯一确定的。 (2)若给定的是第二类边值关系 ∂p =0 01=p2+常数，p1,p2相差一个常数， 虽不唯一，但电场E是唯一确定的。 西安电子科技大学

西安电子科技大学   0 S 1   2 （1）若给定的是第一类边值关系 即常数为零。 电场唯一确定且 电势也是唯一确定的。 虽不唯一，但电场  0   S n  1   2  1 2  , E  （2）若给定的是第二类边值关系 常数， 相差一个常数， 是唯一确定的。 静电场

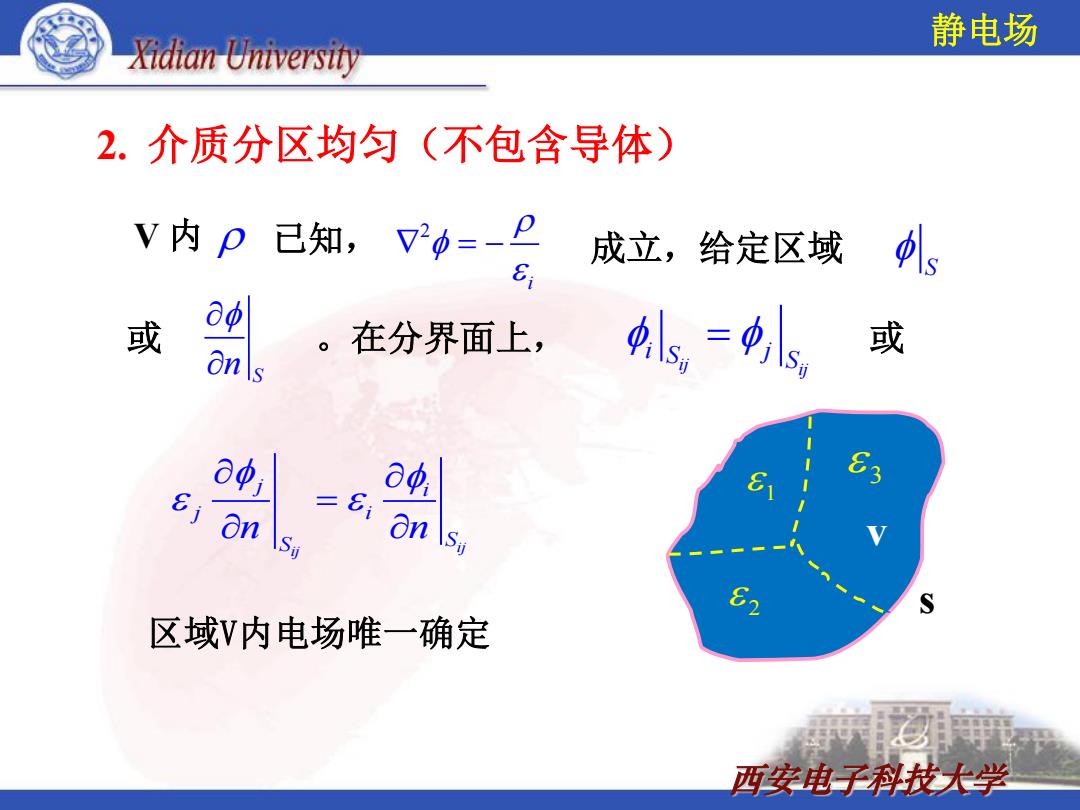
Xidian University 静电场 2.介质分区均匀（不包含导体） V内p已知，v0=-P 成立，给定区域 s 或 ao 。在分界面上， on\s ,=儿 或 0φ， a血 8j on \Sa on \s S 区域V内电场唯一确定 ②用 西安电子科技大学

西安电子科技大学 2. 介质分区均匀（不包含导体）  2 i       S  n S   ij ij i j S S    ij ij j i j i n n S S          已知， 成立，给定区域 或 。在分界面上， 或 V 内 s v 1  2  3  区域V内电场唯一确定 静电场

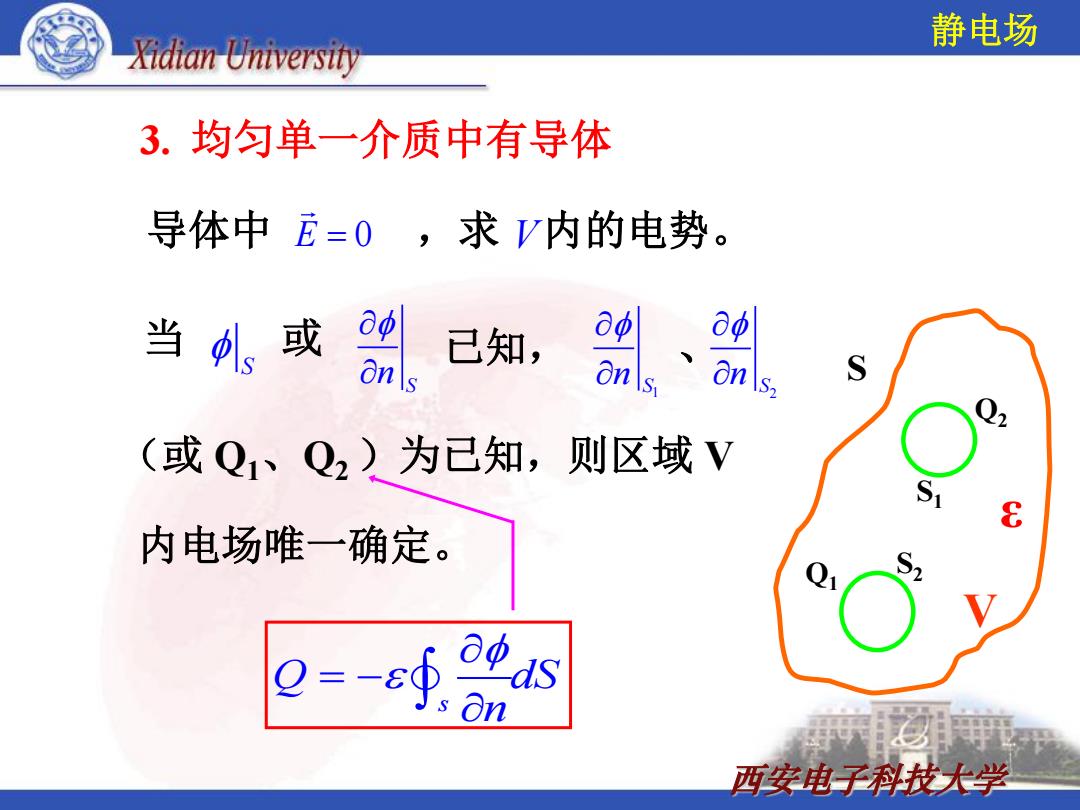
Xidian Universit 静电场 3.均匀单一介质中有导体 导体中E=0,求V内的电势。 当1。或 已知， aφ 8o S (或Q1、Q2)为已知，则区域V 内电场唯一确定。 Q∮s 西安电子科技大学

西安电子科技大学 3. 均匀单一介质中有导体 Q2 Q1 ε S S1 S2 V （或 Q1、Q2 ）为已知，则区域 V S  n S   1 n S   2 n S   或 已知， 、 内电场唯一确定。 当 导体中 E  0 ，求 V 内的电势。 s Q dS n        静电场