《电磁场理论》课程电子教案（讲义）第二章 电磁场的基本规律

解：设圆环的半径为，流过的电流为。为计算方便取线电流圆环位于xOy平面上， 则所求场点为P(0心z,如图所示采用圆柱坐标系，圆环上的电流元为d'=,ad0,其 位置矢量为=，4，而场点P的位置矢量为=，故得 F-F=e.=-a.F-=('ta) Idl'x(F-F)=e lad'x(e.=-e a) =e lazdo'+e.la'do 轴线上任一点P(0,0,z)的磁感应强度为 Z)=42:+ea 2+a3w 由于"e.d-e.cs+e,smw=0 所以 2e2+a23 可见，线电流圆环轴线上的磁感应强度只有轴向分量，这是因为圆环上各对称点处的电流元在 场点P产生的磁感应强度的径向分量相互抵消。 在圆环的中心点上，z=0,磁感应强度最大，即 A0=E岩 当场点P远离圆环，即2>a时，因（+)P己，故 8-6. 2.3.2恒定磁场的散度和旋度 1.恒定磁场的散度与磁通连续性原理 恒定场的散度（徽分形式） V.B)=0 磁通连续性原理（积分形式） 人BG)d5=0 磁通连续性原理表明：恒定磁场是无源场，磁感应线是无起点和终点的闭合曲线。 2.恒定磁场的旋度与安培环路定理 恒定磁场的旋度（微分形式） V×B()=4oJ()

11 解：设圆环的半径为 a，流过的电流为 I。为计算方便取线电流圆环位于 xOy 平面上， 则所求场点为 P (0, 0, z ) , 如图 所示。采用圆柱坐标系，圆环上的电流元为 Idl  = e Iad   , 其 位置矢量为 r ea    = ，而场点 P 的位置矢量为 r e zz    = ，故得 2 1 2 2 r r e z e a, r r (z a ) −  = z − −  = +        Idl (r r ) e Iad (e z e a)   z         −  =  − = e Iazd+ e Ia d z   2 轴线上任一点 P ( 0, 0, z )的磁感应强度为       + + =  d z a Ia e z e a B Z z 2 0 2 3 2 2 0 ( ) 4 ( )    由于 ( cos sin ) 0 2 0 2 0  =  +   =         ed ex ey d    ，所以 2 3 2 2 2 0 2 0 2 3 2 2 0 ( ) 2( ) 4 ( ) z a Ia d z a Ia e a B z z +  = + =         可见，线电流圆环轴线上的磁感应强度只有轴向分量，这是因为圆环上各对称点处的电流元在 场点 P 产生的磁感应强度的径向分量相互抵消。 在圆环的中心点上，z = 0，磁感应强度最大，即 a I B ez 2 (0) 0   = 当场点 P 远离圆环，即 z >> a 时，因 2 2 3 2 3 (z + a )  z ，故 3 2 0 2z Ia B ez    = 2.3.2 恒定磁场的散度和旋度 1. 恒定磁场的散度与磁通连续性原理 恒定场的散度（微分形式） B(r) = 0   磁通连续性原理（积分形式） ( )d = 0 S B r S    磁通连续性原理表明：恒定磁场是无源场，磁感应线是无起点和终点的闭合曲线。 2. 恒定磁场的旋度与安培环路定理 恒定磁场的旋度（微分形式） ( ) ( ) 0 B r J r      = 

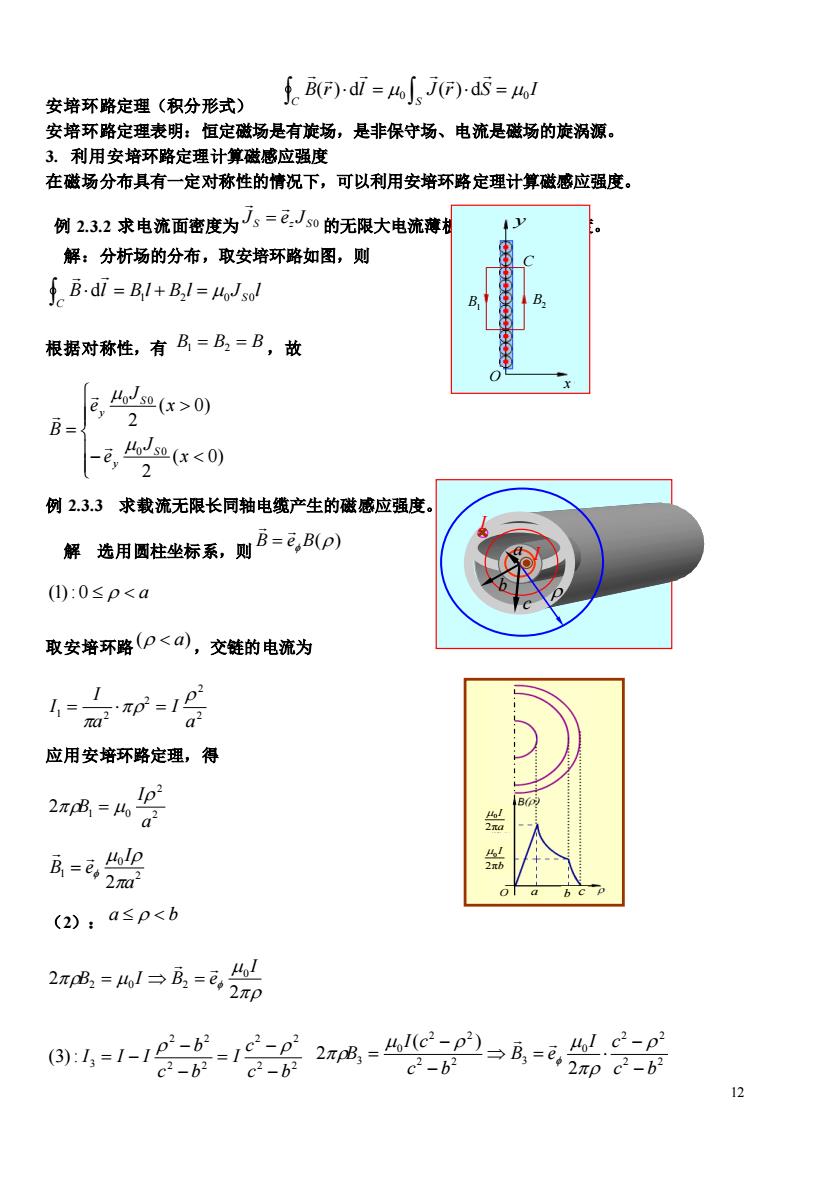
fB()di=「nJ)dS=h1 安培环路定理（积分形式） 安培环路定理表明：恒定磁场是有旋场，是非保守场、电流是磁场的旋涡源。 3.利用安培环路定理计算磁感应强度 在磁场分布具有一定对称性的情况下，可以利用安培环路定理计算磁感应强度。 例2.32求电流面密度为J,=已J0的无限大电流薄利 解：分析场的分布，取安培环略如图，则 fB-dT=BI+B.1=Hosol 根据对称性，有B=B=B,故 E血x>0) B= 2 ,<0 例2.3.3求载流无限长同轴电缆产生的磁感应强度。 解选用圈柱坐标系，则B=已，B(p) ():0≤p<a 取安培环路(p<）,交链的电流为 47号 1 应用安培环略定理，得 2成=%g A=元5g (2):a≤p<b 2成=w1兵=品制 64-答 2π8，=41c-p→A=ec-P c2-b2 2πpc2-b1 12

12 安培环路定理（积分形式） B r l J r S I C S 0 d 0 ( )d =  ( ) =          安培环路定理表明：恒定磁场是有旋场，是非保守场、电流是磁场的旋涡源。 3. 利用安培环路定理计算磁感应强度 在磁场分布具有一定对称性的情况下，可以利用安培环路定理计算磁感应强度。 例 2.3.2 求电流面密度为 S z S 0 J e J   = 的无限大电流薄板产生的磁感应强度。 解：分析场的分布，取安培环路如图，则 B l B l B l J l S C d = 1 + 2 = 0 0     根据对称性，有 B1 = B2 = B ，故        −   = ( 0) 2 ( 0) 2 0 0 0 0 x J e x J e B S y S y      例 2.3.3 求载流无限长同轴电缆产生的磁感应强度。 解 选用圆柱坐标系，则 () B eB   = (1): 0    a 取安培环路 (  a) ，交链的电流为 2 2 2 1 2 a I a I I     =  = 应用安培环路定理，得 2 2 2 1 0 a I B   =  2 0 1 2 a I B e       = （2）： a    b        2 2 0 2 0 2 I B I B e   =  = 2 2 2 2 2 2 2 2 3 (3): c b c I c b b I I I − − = − − = −   2 2 2 2 0 2 2 3 2 2 0 3 2 ( ) 2 c b I c B e c b I c B − −  =  − − =            C B1 B2 O x y a b c  I I a b c 0 2π I b  0 2π I a  O