Computer Number Representation Sign(s) Exponent (e) Fraction (f) Value 0 00.00 00.00 +0 00.01 Positive Denormalized Real 0 00.00 ... 0.f×2(-b+) 11.11 00.01 Positive Normalized Real XX..XX 1.f×2e-b) 11.10 11.11 00.00 +INF 00.01 11.11 SNaN 01.11 10.00 11..11 QNaN 11.11 口回1元,4元t至0QC Weihua Gu (Shanghai Jiao Tong University) Computational Physics Chapter 1 14/09/2015141103
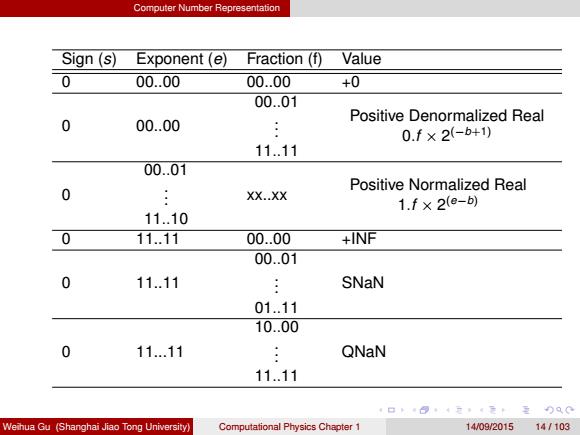
Computer Number Representation Sign (s) Exponent (e) Fraction (f) Value 0 00..00 00..00 +0 0 00..00 00..01 . . . 11..11 Positive Denormalized Real 0.f × 2 (−b+1) 0 00..01 . . . 11..10 xx..xx Positive Normalized Real 1.f × 2 (e−b) 0 11..11 00..00 +INF 0 11..11 00..01 . . . 01..11 SNaN 0 11...11 10..00 . . . 11..11 QNaN Weihua Gu (Shanghai Jiao Tong University) Computational Physics Chapter 1 14/09/2015 14 / 103
Computer Number Representation Sign(s) Exponent (e) Fraction (f) Value 00.00 00.00 -0 00.01 Negative Denormalized Real 00.00 -0.f×2-b41) 11.11 00.01 Negative Normalized Real XX..XX -1.f×2(e-) 11.10 11.11 00.00 -INF 00.01 11.11 SNaN 01.11 10.00 11..11 QNaN 11.11 ¥口,4元4元卡重)90 Weihua Gu (Shanghai Jiao Tong University) Computational Physics Chapter 1 1409201515/103
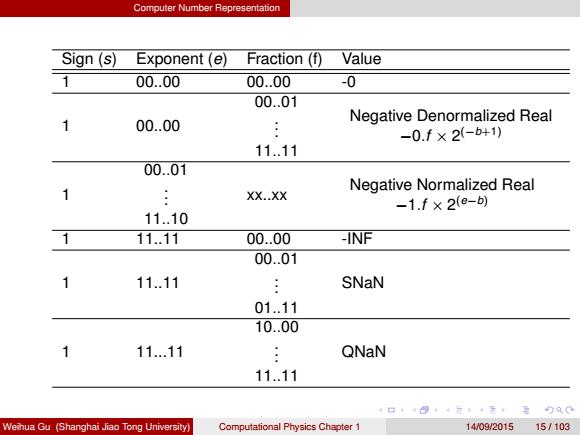
Computer Number Representation Sign (s) Exponent (e) Fraction (f) Value 1 00..00 00..00 -0 1 00..00 00..01 . . . 11..11 Negative Denormalized Real −0.f × 2 (−b+1) 1 00..01 . . . 11..10 xx..xx Negative Normalized Real −1.f × 2 (e−b) 1 11..11 00..00 -INF 1 11..11 00..01 . . . 01..11 SNaN 1 11...11 10..00 . . . 11..11 QNaN Weihua Gu (Shanghai Jiao Tong University) Computational Physics Chapter 1 14/09/2015 15 / 103

Computer Number Representation Example 1:The Largest The largest positive normal floating-point number possible for a 32-bit machine: Xax=01111111011111111111111111111111 =(0)(11111110)(11111111111111111111111) s=0.e=11111110=254.p=e-127=127 f=1.11111111111111111111111=1+0.5+0.25+.2 =(-1)5×1f×20=-1四2×21273.4×1038 口回1元,4元t至0QC Weihua Gu (Shanghai Jiao Tong University) Computational Physics Chapter 1 14/09/201516/103
Computer Number Representation Example 1: The Largest The largest positive normal floating-point number possible for a 32-bit machine: Xmax = 01111 1110 1111 1111 1111 1111 1111 111 = (0) (1111 1110) (1111 1111 1111 1111 1111 111) s = 0, e = 1111 1110 = 254, p = e − 127 = 127 f = 1.1111 1111 1111 1111 1111 111 = 1 + 0.5 + 0.25 + · · · ' 2 ⇒ (−1) s × 1.f × 2 p=e−127 ' 2 × 2 127 ' 3.4 × 1038 Weihua Gu (Shanghai Jiao Tong University) Computational Physics Chapter 1 14/09/2015 16 / 103

Computer Number Representation Example 1:The Largest The largest positive normal floating-point number possible for a 32-bit machine: Xmax=01111111011111111111111111111111 =(0)(11111110)(11111111111111111111111) s=0.e=11111110=254.p=e-127=127 f=1.11111111111111111111111=1+0.5+0.25+..2 →(-1)5×1.f×2=e-12~2×21273.4×1038 口回1元,4元t至0QC Weihua Gu (Shanghai Jiao Tong University) Computational Physics Chapter 1 14/09/201516/103
Computer Number Representation Example 1: The Largest The largest positive normal floating-point number possible for a 32-bit machine: Xmax = 01111 1110 1111 1111 1111 1111 1111 111 = (0) (1111 1110) (1111 1111 1111 1111 1111 111) s = 0, e = 1111 1110 = 254, p = e − 127 = 127 f = 1.1111 1111 1111 1111 1111 111 = 1 + 0.5 + 0.25 + · · · ' 2 ⇒ (−1) s × 1.f × 2 p=e−127 ' 2 × 2 127 ' 3.4 × 1038 Weihua Gu (Shanghai Jiao Tong University) Computational Physics Chapter 1 14/09/2015 16 / 103

Computer Number Representation Example 1:The Largest The largest positive normal floating-point number possible for a 32-bit machine: Xmax=01111111011111111111111111111111 =(0)(11111110)(11111111111111111111111) S=0,e=11111110=254,p=e-127=127 f=1.11111111111111111111111=1+0.5+0.25+··≈2 →(-1)°×1.f×2=e-127≈2×2127≈3.4×1038 口回1元,4元t至0QC Weihua Gu (Shanghai Jiao Tong University) Computational Physics Chapter 1 14/09/201516/103
Computer Number Representation Example 1: The Largest The largest positive normal floating-point number possible for a 32-bit machine: Xmax = 01111 1110 1111 1111 1111 1111 1111 111 = (0) (1111 1110) (1111 1111 1111 1111 1111 111) s = 0, e = 1111 1110 = 254, p = e − 127 = 127 f = 1.1111 1111 1111 1111 1111 111 = 1 + 0.5 + 0.25 + · · · ' 2 ⇒ (−1) s × 1.f × 2 p=e−127 ' 2 × 2 127 ' 3.4 × 1038 Weihua Gu (Shanghai Jiao Tong University) Computational Physics Chapter 1 14/09/2015 16 / 103