LLL condition:]:A→(0,+o) VS A:asPr[nAESA], HA∈A:Pr[A]≤ MA s T+(A) ∑ΠA Indep.IES AEl Recursive bounds: S∈A,B∈S: qsB≤9s+Pr(B)Asr+(B) S∈l,B度S: UBy≥s+Pr(B)sUr+(B) usu(B) ∑Πa+∑Π Indep.IsSA∈ B∈Indep.ICSUB A∈l =4s+B ∑ Idep.iEs\r+(B)AEi I≤S B∈ISSU{B)→I\{B}SS\+(B) Indep.I∈SU{B}
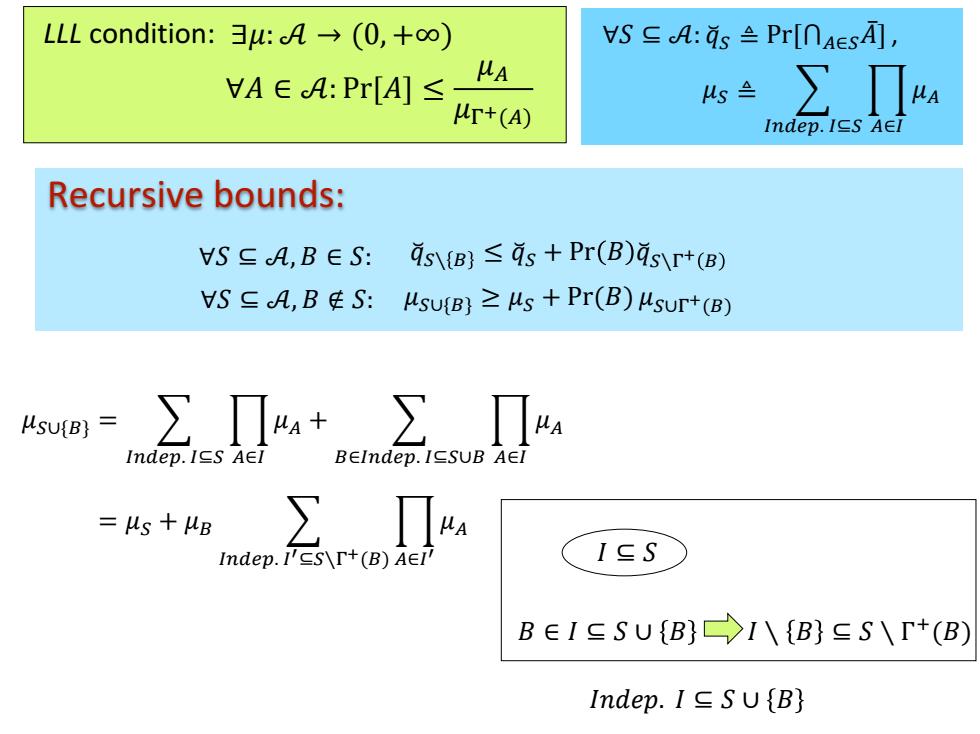
∀𝑆 ⊆ 𝒜: 𝑞෬𝑆 ≜ Pr[⋂𝐴∈𝑆𝐴ҧ], 𝜇𝑆 ≜ 𝐼𝑛𝑑𝑒𝑝. 𝐼⊆𝑆 ෑ 𝐴∈𝐼 𝜇𝐴 Recursive bounds: 𝑞෬𝑆∖ 𝐵 ≤ 𝑞෬𝑆 + Pr 𝐵 𝑞෬𝑆∖Γ + 𝐵 𝜇𝑆∪{𝐵} ≥ 𝜇𝑆 + Pr(𝐵) 𝜇𝑆∪Γ + ∀𝑆 ⊆ 𝒜 (𝐵) , 𝐵 ∉ 𝑆: 𝜇𝑆∪{𝐵} = 𝐼𝑛𝑑𝑒𝑝. 𝐼⊆𝑆 ෑ 𝐴∈𝐼 𝜇𝐴 + 𝐵∈𝐼𝑛𝑑𝑒𝑝. 𝐼⊆𝑆∪𝐵 ෑ 𝐴∈𝐼 𝜇𝐴 LLL condition: ∃𝜇: 𝒜 → (0, +∞) ∀𝐴 ∈ 𝒜: Pr[𝐴] ≤ 𝜇𝐴 𝜇Γ+(𝐴) ∀𝑆 ⊆ 𝒜, 𝐵 ∈ 𝑆: = 𝜇𝑆 + 𝜇𝐵 𝐼𝑛𝑑𝑒𝑝. 𝐼 ′⊆𝑆∖Γ+(𝐵) ෑ 𝐴∈𝐼 ′ 𝜇𝐴 𝐼 ⊆ 𝑆 𝐼𝑛𝑑𝑒𝑝. 𝐼 ⊆ 𝑆 ∪ 𝐵 𝐼 ∖ 𝐵 ⊆ 𝑆 ∖ Γ + 𝐵 ∈ 𝐼 ⊆ 𝑆 ∪ 𝐵 (𝐵)
LLL condition::A→(0,+oo) SSA:is≌Pr[n4esA, HA∈A:Pr[A]≤ MA s兰 T+(A) ∑Ia Indep.IES AEl Recursive bounds: S∈A,BeS: 4s\(B)4s +Pr(B)4s\r+(B) VS∈A,BtS: suB≥s+Pr(B)Lsur+(B) 4UB= ∑a+∑Π Indep.IsSA∈l BEIndep.IESUB AEI us uB ∑Πa Indep.I'ES\r+(B)AEI I∈S○ =us +uBus\r+(B) BEI∈SU{B}→I\{B}∈S\T+(B) Indep.I∈SU{B}
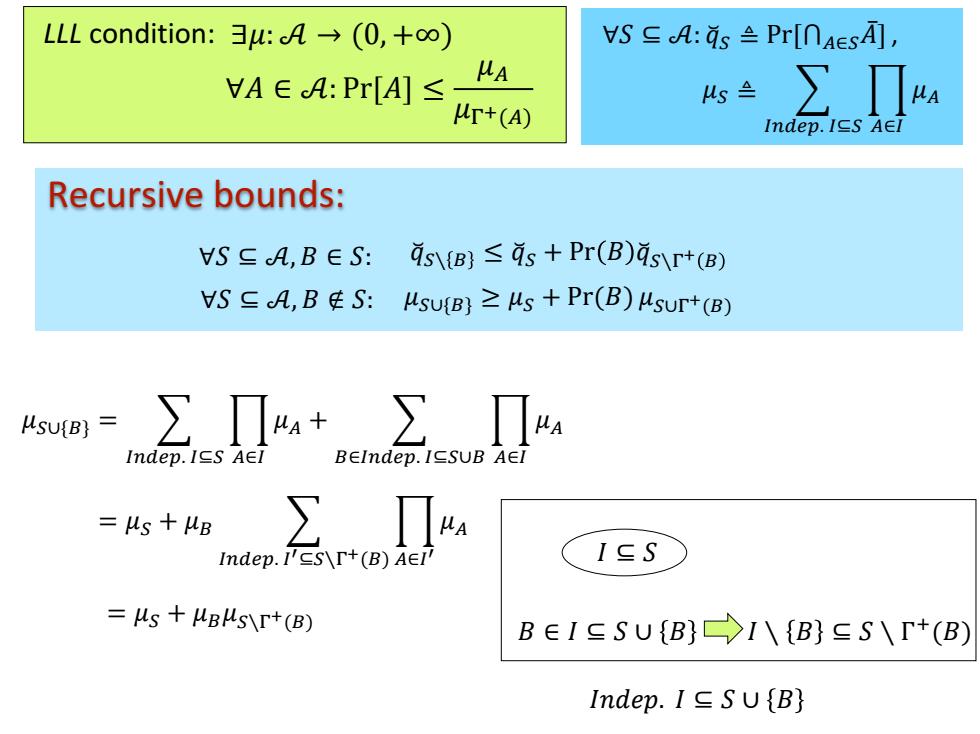
∀𝑆 ⊆ 𝒜: 𝑞෬𝑆 ≜ Pr[⋂𝐴∈𝑆𝐴ҧ], 𝜇𝑆 ≜ 𝐼𝑛𝑑𝑒𝑝. 𝐼⊆𝑆 ෑ 𝐴∈𝐼 𝜇𝐴 Recursive bounds: 𝑞෬𝑆∖ 𝐵 ≤ 𝑞෬𝑆 + Pr 𝐵 𝑞෬𝑆∖Γ + 𝐵 𝜇𝑆∪{𝐵} ≥ 𝜇𝑆 + Pr(𝐵) 𝜇𝑆∪Γ + ∀𝑆 ⊆ 𝒜 (𝐵) , 𝐵 ∉ 𝑆: 𝜇𝑆∪{𝐵} = 𝐼𝑛𝑑𝑒𝑝. 𝐼⊆𝑆 ෑ 𝐴∈𝐼 𝜇𝐴 + 𝐵∈𝐼𝑛𝑑𝑒𝑝. 𝐼⊆𝑆∪𝐵 ෑ 𝐴∈𝐼 𝜇𝐴 LLL condition: ∃𝜇: 𝒜 → (0, +∞) ∀𝐴 ∈ 𝒜: Pr[𝐴] ≤ 𝜇𝐴 𝜇Γ+(𝐴) ∀𝑆 ⊆ 𝒜, 𝐵 ∈ 𝑆: = 𝜇𝑆 + 𝜇𝐵 𝐼𝑛𝑑𝑒𝑝. 𝐼 ′⊆𝑆∖Γ+(𝐵) ෑ 𝐴∈𝐼 ′ 𝜇𝐴 = 𝜇𝑆 + 𝜇𝐵𝜇𝑆∖Γ +(𝐵) 𝐼 ⊆ 𝑆 𝐼𝑛𝑑𝑒𝑝. 𝐼 ⊆ 𝑆 ∪ 𝐵 𝐼 ∖ 𝐵 ⊆ 𝑆 ∖ Γ + 𝐵 ∈ 𝐼 ⊆ 𝑆 ∪ 𝐵 (𝐵)
LLL condition:]:A→(0,+o) ∀SSA:is±Pr[n4esA, VA∈A:Pr[A]≤ 、 A T+(A) Indep.IES AEl Recursive bounds: VS∈L,B∈S: 4s\(B)s 4s +Pr(B)4s\r+(B) VS A,B S:HsU[B)2us+Pr(B)Hsur+(B) usu(B)=us +uBus\r+(B) I∈S BEI∈SU{B}→I\{B}SS\+(B) Indep.ISU{B)
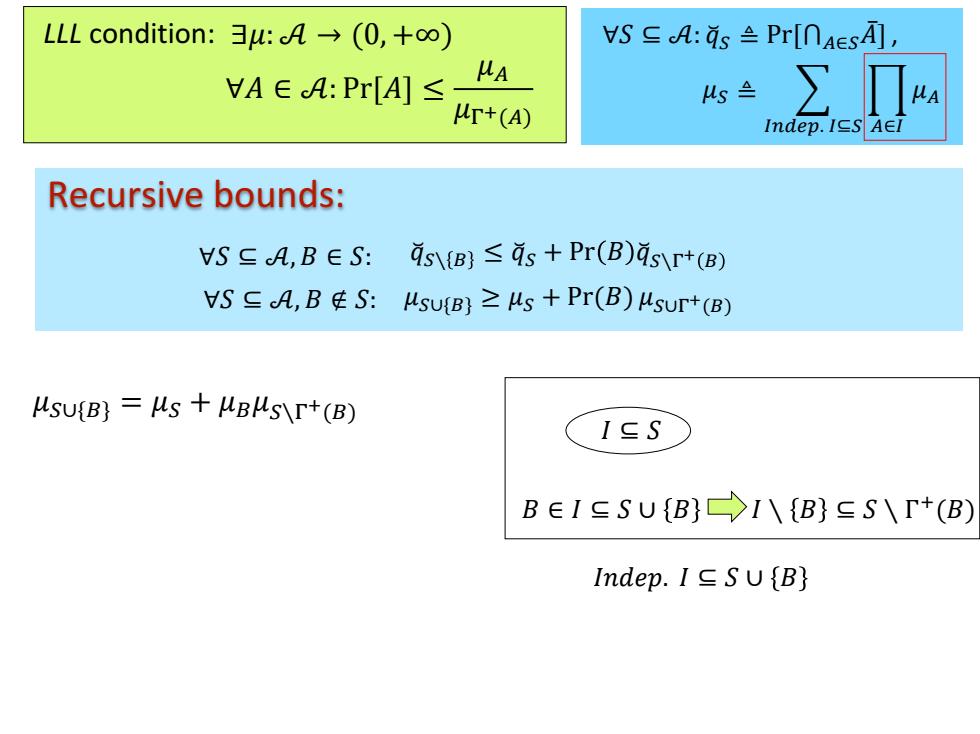
∀𝑆 ⊆ 𝒜: 𝑞෬𝑆 ≜ Pr[⋂𝐴∈𝑆𝐴ҧ], 𝜇𝑆 ≜ 𝐼𝑛𝑑𝑒𝑝. 𝐼⊆𝑆 ෑ 𝐴∈𝐼 𝜇𝐴 Recursive bounds: 𝑞෬𝑆∖ 𝐵 ≤ 𝑞෬𝑆 + Pr 𝐵 𝑞෬𝑆∖Γ + 𝐵 𝜇𝑆∪{𝐵} ≥ 𝜇𝑆 + Pr(𝐵) 𝜇𝑆∪Γ + ∀𝑆 ⊆ 𝒜, 𝐵 ∉ 𝑆: (𝐵) 𝜇𝑆∪{𝐵} = 𝜇𝑆 + 𝜇𝐵𝜇𝑆∖Γ +(𝐵) LLL condition: ∃𝜇: 𝒜 → (0, +∞) ∀𝐴 ∈ 𝒜: Pr[𝐴] ≤ 𝜇𝐴 𝜇Γ+(𝐴) ∀𝑆 ⊆ 𝒜, 𝐵 ∈ 𝑆: 𝐼 ⊆ 𝑆 𝐼𝑛𝑑𝑒𝑝. 𝐼 ⊆ 𝑆 ∪ 𝐵 𝐼 ∖ 𝐵 ⊆ 𝑆 ∖ Γ + 𝐵 ∈ 𝐼 ⊆ 𝑆 ∪ 𝐵 (𝐵)
LLL condition::A→(0,+oo) SSA:is≌Pr[n4esA, HA∈A:Pr[A]≤ MA 4s合 T+(A) ∑a Indep.IES AEI Recursive bounds: S∈A,BeS: 4s\(B)4s +Pr(B)4s\r+(B) S≤A,BtS: USU(B)2 us +Pr(B)usur+(B) usufB)=us uBus\r+(B) I∈S B∈ISSU{B}→I\{B}SS\T+(B) Indep.I∈Su{B}
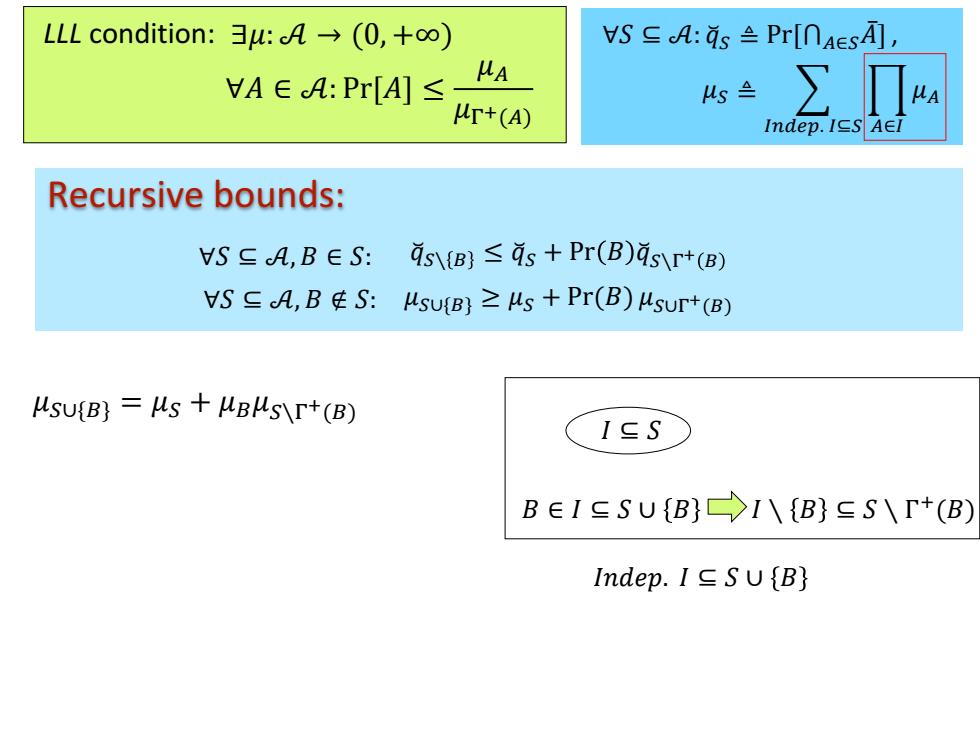
∀𝑆 ⊆ 𝒜: 𝑞෬𝑆 ≜ Pr[⋂𝐴∈𝑆𝐴ҧ], 𝜇𝑆 ≜ 𝐼𝑛𝑑𝑒𝑝. 𝐼⊆𝑆 ෑ 𝐴∈𝐼 𝜇𝐴 Recursive bounds: 𝑞෬𝑆∖ 𝐵 ≤ 𝑞෬𝑆 + Pr 𝐵 𝑞෬𝑆∖Γ + 𝐵 𝜇𝑆∪{𝐵} ≥ 𝜇𝑆 + Pr(𝐵) 𝜇𝑆∪Γ + ∀𝑆 ⊆ 𝒜, 𝐵 ∉ 𝑆: (𝐵) 𝜇𝑆∪{𝐵} = 𝜇𝑆 + 𝜇𝐵𝜇𝑆∖Γ +(𝐵) LLL condition: ∃𝜇: 𝒜 → (0, +∞) ∀𝐴 ∈ 𝒜: Pr[𝐴] ≤ 𝜇𝐴 𝜇Γ+(𝐴) ∀𝑆 ⊆ 𝒜, 𝐵 ∈ 𝑆: 𝐼 ⊆ 𝑆 𝐼𝑛𝑑𝑒𝑝. 𝐼 ⊆ 𝑆 ∪ 𝐵 𝐼 ∖ 𝐵 ⊆ 𝑆 ∖ Γ + 𝐵 ∈ 𝐼 ⊆ 𝑆 ∪ 𝐵 (𝐵)

LLL condition:]:A→(0,+o) ∀SSA:as±Pr[n4esA, VA∈A:Pr[A]≤ A T+(A) ΣΠa Indep.IES AEl Recursive bounds: VS∈L,B∈S: @5\(B)<4s +Pr(B)4s\r+(B) VS≤A,BES:suBy≥s+Pr(B)sUr+(B) usu(B)=us uBus\r+(B) z us +Pr[B]ur+(B)Hs\r+(B)
∀𝑆 ⊆ 𝒜: 𝑞෬𝑆 ≜ Pr[⋂𝐴∈𝑆𝐴ҧ], 𝜇𝑆 ≜ 𝐼𝑛𝑑𝑒𝑝. 𝐼⊆𝑆 ෑ 𝐴∈𝐼 𝜇𝐴 Recursive bounds: 𝑞෬𝑆∖ 𝐵 ≤ 𝑞෬𝑆 + Pr 𝐵 𝑞෬𝑆∖Γ + 𝐵 𝜇𝑆∪{𝐵} ≥ 𝜇𝑆 + Pr(𝐵) 𝜇𝑆∪Γ + ∀𝑆 ⊆ 𝒜, 𝐵 ∉ 𝑆: (𝐵) 𝜇𝑆∪{𝐵} = 𝜇𝑆 + 𝜇𝐵𝜇𝑆∖Γ +(𝐵) ≥ 𝜇𝑆 + Pr[𝐵] 𝜇Γ +(𝐵)𝜇𝑆∖Γ +(𝐵) LLL condition: ∃𝜇: 𝒜 → (0, +∞) ∀𝐴 ∈ 𝒜: Pr[𝐴] ≤ 𝜇𝐴 𝜇Γ+(𝐴) ∀𝑆 ⊆ 𝒜, 𝐵 ∈ 𝑆: