
7.2菲克定律的应用 在扩散系统中,若对于任一体积元,在任一时刻流 入的物质量与流出的物质量相等,即任一点的浓度 不随时间而变化,-0,则称这种状态为稳态扩散
7.2 菲克定律的应用 在扩散系统中,若对于任一体积元,在任一时刻流 入的物质量与流出的物质量相等,即任一点的浓度 不随时间而变化, =0,则称这种状态为稳态扩散

工程中要解决的涉及扩散的实际问题有两类: (1)求解通过某一曲面(如平面、柱面、球面等) 的通量J,以解决单位时间通过该面的物质流量 dm/dt=AJ: (2)求解浓度分布C(x,),以解决材料的组分及显 微结构控制。 为此需要分别求解菲克第一定律及菲克第二定律
工程中要解决的涉及扩散的实际问题有两类: (1)求解通过某一曲面(如平面、柱面、球面等) 的通量J,以解决单位时间通过该面的物质流量 dm/dt=AJ; (2)求解浓度分布 C(x, t),以解决材料的组分及显 微结构控制。 为此需要分别求解菲克第一定律及菲克第二定律
7.2.1稳态扩散及其应用 7.2.1.1一维稳态扩散 考虑氢通过金属膜的扩散。如图7.6所示,金属膜的厚 度为δ,取x轴垂直于膜面。 p2>p1 翠 不透气的壁 金属薄膜 (a) (6) 图7.6氢对金属膜的一维稳态扩散
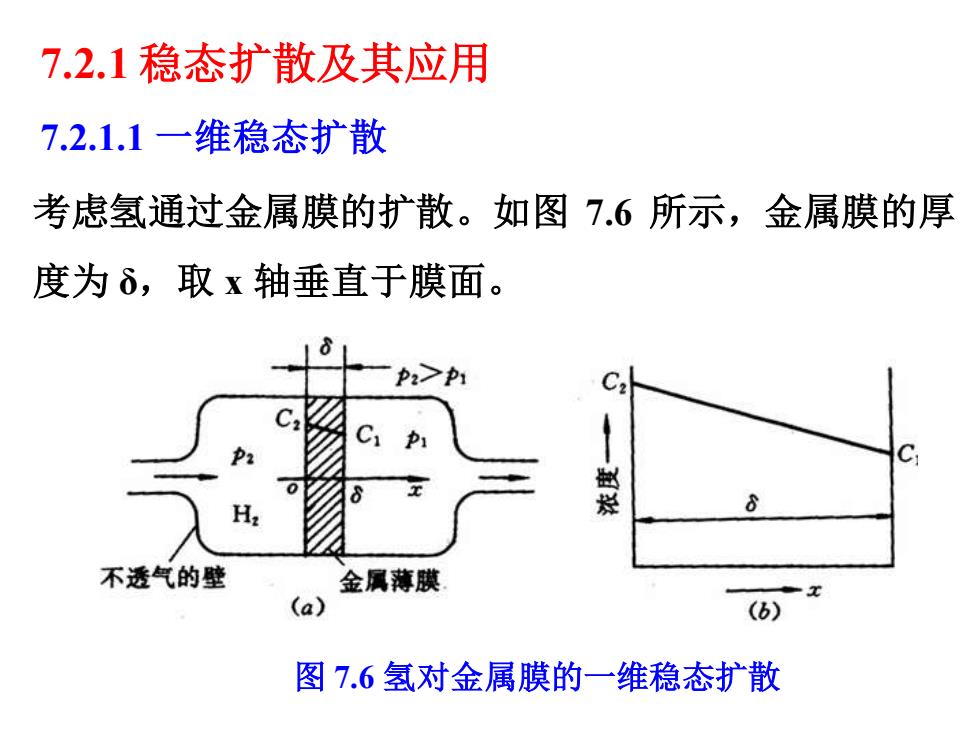
7.2.1 稳态扩散及其应用 7.2.1.1 一维稳态扩散 考虑氢通过金属膜的扩散。如图 7.6 所示,金属膜的厚 度为 δ,取 x 轴垂直于膜面。 图 7.6 氢对金属膜的一维稳态扩散

◆金属膜两边供气与抽气同时进行,一面保持高而恒定的压力P2, 另一面保持低而恒定的压力p1。扩散一定时间以后,金属膜中建 立起稳定的浓度分布。 氢的扩散包括氢气吸附于金属膜表面,氢分子分解为原子、离 子,以及氢离子在金属膜中的扩散等过程。 达到稳态扩散时的边界条件: Cx=0=C2 C=5=C1 C1、C,可由热解反应H2→H+H的平衡常数K确定,根据K的定义: K- 产物活度积 反应物活度积
氢的扩散包括氢气吸附于金属膜表面,氢分子分解为原子、离 子,以及氢离子在金属膜中的扩散等过程。 达到稳态扩散时的边界条件: C1、C2可由热解反应H2→H+H的平衡常数K确定,根据K的定义: ◆ 金属膜两边供气与抽气同时进行,一面保持高而恒定的压力p2, 另一面保持低而恒定的压力 p1。扩散一定时间以后,金属膜中建 立起稳定的浓度分布

设氢原子的浓度为C,则 K= C·C 卫 即 C=Kp=S (7.20) 式(7.20)中S为西佛特(Sievert).定律常数,其物理 意义是,当空间压力p=1MPa时金属表面的溶解浓度。 式(7.20)表明,金属表面气体的溶解浓度与空间压力 的2次方根成正比
设氢原子的浓度为 C,则 即 (7.20) 式(7.20)中 S 为西佛特(Sievert)定律常数,其物理 意义是,当空间压力 p=1 MPa 时金属表面的溶解浓度。 式(7.20)表明,金属表面气体的溶解浓度与空间压力 的 2 次方根成正比