7.1.2.1一维扩散 如图7.4所示,在扩散方向上取体积元A△x,J和 Jx+△x分别表示流入体积元及流出体积元的扩散通量, △x x+△x 图7.4扩散流通过微小体积的情况
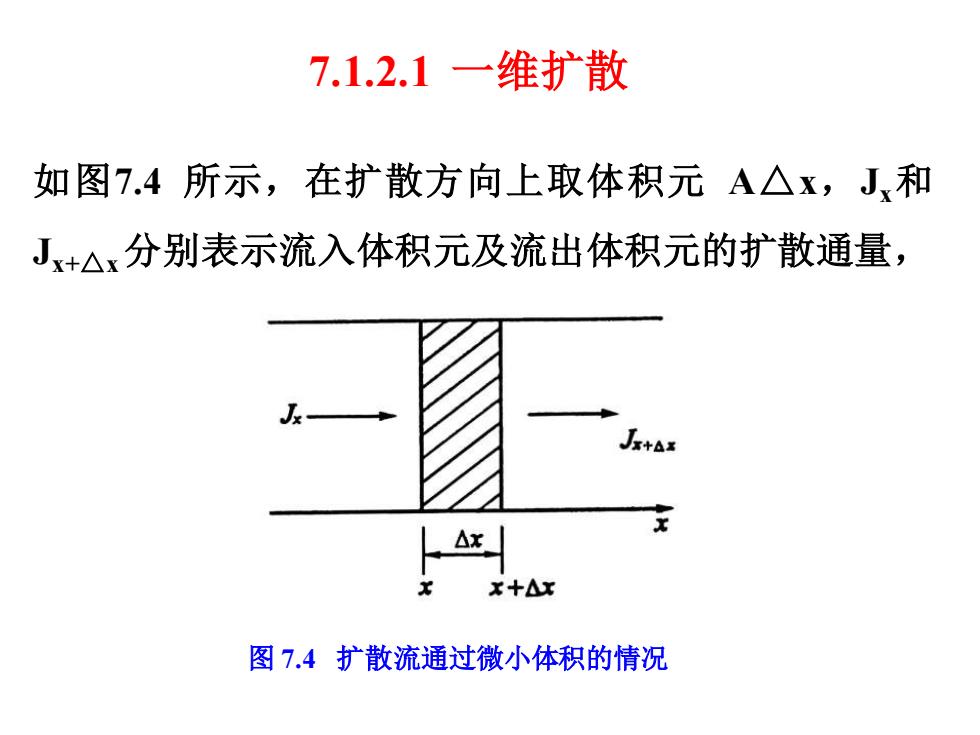
7.1.2.1 一维扩散 如图7.4 所示,在扩散方向上取体积元 A△x,Jx和 Jx+△x分别表示流入体积元及流出体积元的扩散通量, 图 7.4 扩散流通过微小体积的情况

则在△t时间内,体积元中扩散物质的累积量为: △m=(JxA-J+AxA)△t 则有 △m =J:二J+ △xA△t △x
则在 △t 时间内,体积元中扩散物质的累积量为: 则有

C 0 随t增加 随t增加 浓度升高,/ 浓度降低 J=-D3C 器 扩散方向与浓度 降低的方向相一致 图7.5菲克第一、第二定律的关系
图 7.5 菲克第一、第二定律的关系

从形式上看,菲克第二定律表示,在扩散过程中某点 浓度随时间的变化率与浓度分布曲线在该点的二阶导 数成正比。 >若曲线在该点的二阶导数之大于0,即曲线为四形, 则该点的浓度会随时间的增加而增加,即>0: a2C >若曲线在该点的二阶导数x小于0,即曲线为凸形, 则该点的浓度会随时间的增加而降低,即形<0。 而菲克第一定律表示扩散方向与浓度降低的方向相一 致
从形式上看,菲克第二定律表示,在扩散过程中某点 浓度随时间的变化率与浓度分布曲线在该点的二阶导 数成正比。 ➢ 若曲线在该点的二阶导数 大于0,即曲线为凹形, 则该点的浓度会随时间的增加而增加,即 ; ➢ 若曲线在该点的二阶导数 小于0,即曲线为凸形, 则该点的浓度会随时间的增加而降低,即 。 而菲克第一定律表示扩散方向与浓度降低的方向相一 致

菲克第一、第二定律本质上是一个定律, 均表明扩散的结果总是使不均匀体系均 匀化,由非平衡逐渐达到平衡
菲克第一、第二定律本质上是一个定律, 均表明扩散的结果总是使不均匀体系均 匀化,由非平衡逐渐达到平衡