
第/八章晶体结构的几何理论 ▣晶体外形上的对称要素一共9种 目 5种对称轴 L1;L2;L3;L4,L6 目 2种旋转反伸轴 L4,L6 目 对称面 P ▣对称中心 Crystallography 2东理2火深 HANDONG UNIVERSITY OF TECHNOLO
Crystallography 第八章晶体结构的几何理论 晶体外形上的对称要素—共9种 5种对称轴 2种旋转反伸轴 对称面 对称中心 L1; L2 ; L3; L4; L6 Li 4;Li 6 C P 6

第/八章晶体结枸的几何理论 ▣对称要素的组合 ▣组合定理5个 对称型32种 目 定理1:Ln+P/=LnP ▣定理2:Ln+L2=LnnL2 口定理3:L"偶+PL=LnPC 口定理4:Li"偶+L2(或P=i(n/2L2nl2)P Li"商+L2(或P)=LinnL2nP Crystallography 东露军
Crystallography 第八章晶体结构的几何理论 组合定理5个 对称型32种 对称要素的组合 定理1:Ln + P∥ = LnnP 定理2:Ln + L2 ⊥= Ln nL2 定理3:Ln (偶) +P⊥ = Ln PC 定理4:Li n (偶)+ L2 ⊥(或P∥) = Li n (n/2)L2 (n/2)P Li n (奇)+ L2 ⊥(或P∥) = Li n nL2nP 7
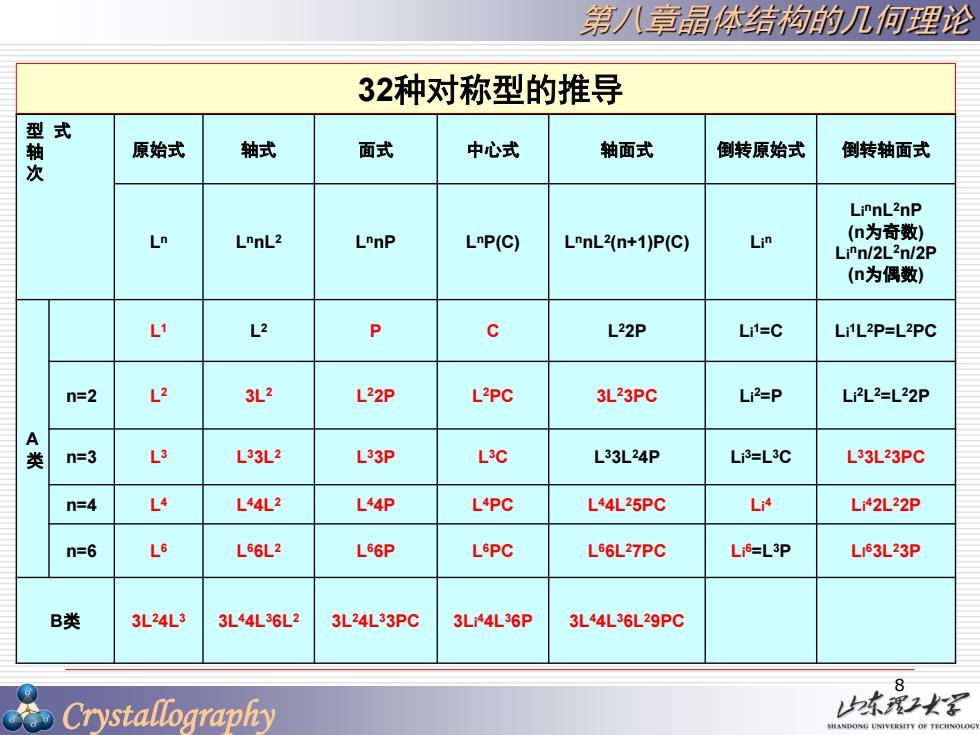
第/八章晶体结构的儿何理论 32种对称型的推导 型式 原始式 轴式 面式 中心式 轴面式 倒转原始式 倒转轴面式 LimnL2nP Ln LonL2 LrnP LnP(C) LmnL2(n+1)P(C) Lin (n为奇数) Li"n/2L2n/2P (n为偶数) L1 L2 P c L22P Li=C Li1L2P=L2PC n=2 〈e 3L2 L22P L2PC 3L23PC Li2=P Li2L2=L22P A n=3 L3 L33L2 L33P L3C L33L24P Li3=L3C L33L23PC n=4 L4 L44L2 L44P L4PC L44L25PC Li4 Li42L22P n=6 L6 L66L2 L66P L6PC L66L27PC Li6=L3P LI63L23P B类 3L24L3 3L44L36L2 3L24L33PC 3L44L36P 3L44L36L29PC Crystallography 本爱2火深 HANDONG UNIVERSITY OF TECHNOLO
Crystallography 第八章晶体结构的几何理论 32种对称型的推导 型 式 轴 次 原始式 轴式 面式 中心式 轴面式 倒转原始式 倒转轴面式 L n L nnL2 L nnP L nP(C) L nnL2 (n+1)P(C) Li n Li nnL2nP (n为奇数) Li nn/2L2n/2P (n为偶数) A 类 L 1 L 2 P C L 22P Li 1=C Li 1L 2P=L2PC n=2 L 2 3L2 L 22P L 2PC 3L23PC Li 2=P Li 2L 2=L22P n=3 L 3 L 33L2 L 33P L 3C L 33L24P Li 3=L3C L 33L23PC n=4 L 4 L 44L2 L 44P L 4PC L 44L25PC Li 4 Li 42L22P n=6 L 6 L 66L2 L 66P L 6PC L 66L27PC Li 6=L3P LI 63L23P B类 3L24L3 3L44L36L2 3L24L33PC 3Li 44L36P 3L44L36L29PC 8

第/八章晶体结枸的几何理论 口由对称要素联系起来的一组或几组晶面 ▣结晶单形146种 ▣几何单形47种 ▣聚形及单形相聚的条件 9 Crystallography 床爱军
Crystallography 第八章晶体结构的几何理论 结晶单形146种 几何单形47种 聚形及单形相聚的条件 由对称要素联系起来的一组或几组晶面 9

第/八章晶体结构的几何理论 口晶体定向与结晶符号 晶面、晶棱与晶轴的关系 ▣晶面符号与单形符号 口晶棱符号与晶带符号 ▣对称型的国际符号 10 Crystallography 本理2火军 HANDONG UNIVERSITY OF TECHNOLO
Crystallography 第八章晶体结构的几何理论 晶面符号与单形符号 晶棱符号与晶带符号 对称型的国际符号 晶体定向与结晶符号 -晶面、晶棱与晶轴的关系 10