
b b P(ab)P(a) P(a b,)a P(ab)Palb)…P(a21b,) [Pv]= 42 P(a,b)P(a,b2).P(a,b)a, []=[P]IPx] 第三章信道模型和信道 信息理论与编码 11 容量
第三章 信道模型和信道 容量 信息理论与编码 11 1 2 1 1 1 2 1 1 2 1 2 2 2 2 | 1 2 ( | ) ( | ) ( | ) ( | ) ( | ) ( | ) [ ] ( | ) ( | ) ( | ) s ss X Y r r r s r b b b P a b P a b P a b a P a b P a b P a b a P P a b P a b P a b a | [ ] [ ][ ] P P P Y X YX
4、信道的疑义度、散布度和平均互信息 I(X:Y)=H(X)-H(X Y) X的实用信息损失的部分 H(X|Y)既代表收到输出Y后对输入X还 存有的疑义,又代表信道在传输过程中的 信息损失,因此,通常把H(XY)称为信道 的疑义度或损失熵。 第三章信道模型和信道 信息理论与编码 12 容量
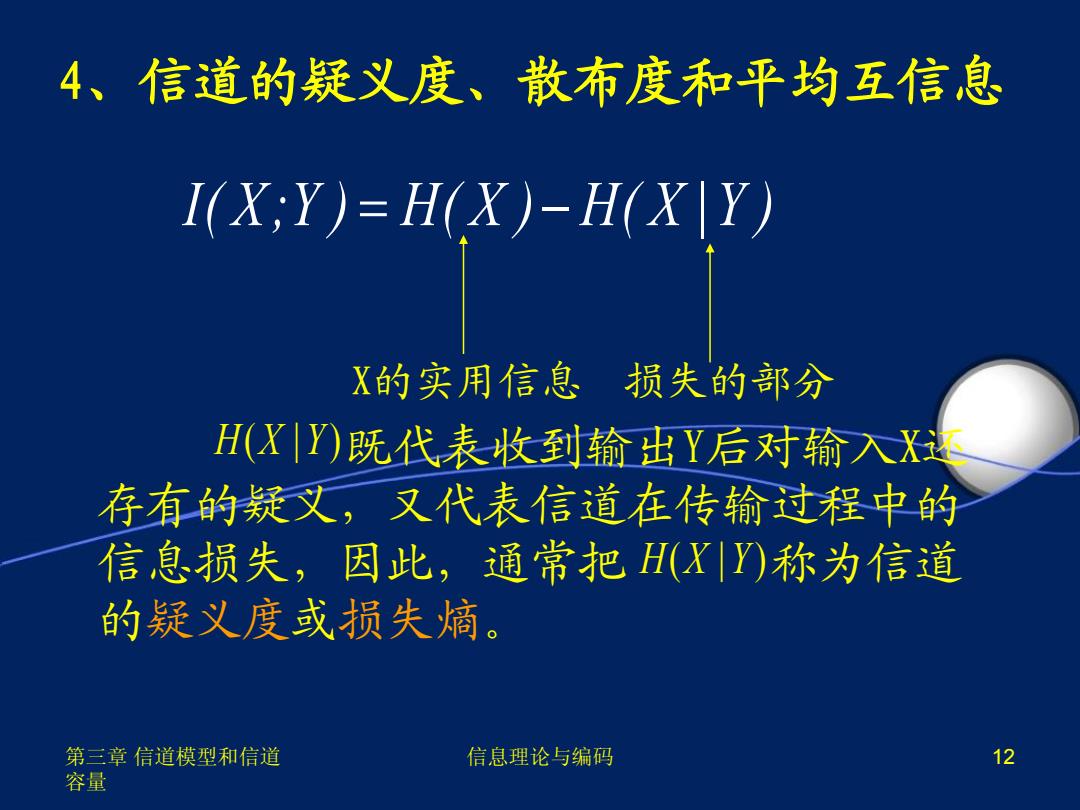
第三章 信道模型和信道 容量 信息理论与编码 12 4、信道的疑义度、散布度和平均互信息 X的实用信息 损失的部分 既代表收到输出Y后对输入X还 存有的疑义,又代表信道在传输过程中的 信息损失,因此,通常把 称为信道 的疑义度或损失熵。 I( X ;Y ) H( X ) H( X |Y ) H X Y ( | ) H X Y ( | )

X)-ΣRa,a1-∑u,)enai i=l i=l 11j=1 -2s交emn-变鸭mra 无损信道:损失熵为零的信道 第三章信道模型和信道 信息理论与编码 13 容量
第三章 信道模型和信道 容量 信息理论与编码 13 无损信道:损失熵为零的信道。 1 1 1 1 1 1 1 1 ( | ) ( , ) ( | ) ( , )log ( | ) 1 ( ) ( | )log ( ) ( | ) ( | ) r s r s i j i j i j i j i j i j s r s j i j j j j i j i j H X Y P a b I a b P a b P a b P b P a b P b H X Y b P a b