
第2章信息的度量 7/21/20101:03PM 信息理论与编码 1
7/21/2010 1:03 PM 信息理论与编码 1 第2章 信息的度量

主要内容 1、信源的数学模型及 7、离散有记忆信源的熵 分类 8、马尔可夫信源的信息 2、信息量及其性质 熵 3、离散信源的熵及性质 9、离散信源的信息(速 4、联合熵和条件熵 率和信息含 5、平均互信息量及其性 量效率 质 10、连续随机变量下的 6、扩展信源 熵和平均互信息量 第2章信息的度量 信息理论与编码 2
第2章 信息的度量 信息理论与编码 2 主要内容 1 、信源的数学模型及 分类 2、信息量及其性质 3、离散信源的熵及性质 4、联合熵和条件熵 5、平均互信息量及其性 质 6、扩展信源 7、离散有记忆信源的熵 8、马尔可夫信源的信息 熵 9、离散信源的信息(速) 率和信息含 量效率 10、连续随机变量下的 熵和平均互信息量

1、信源的数学模型及分类 根据参数集和值域是离散集合还是连续 区间,可将信源分为四类: (1)时间离散空间离散信源 (2)时间离散空间连续信源 (3)时间连续空间离散信源 (4)时间连续空间连续信源 简单的表示: 空间离散信源→离散信源 空间连续信源→连续信源 第2章信息的度量 信息理论与编码 3
第2章 信息的度量 信息理论与编码 3 1 、信源的数学模型及分类 根据参数集和值域是离散集合还是连续 区间,可将信源分为四类: (1) 时间离散空间离散信源 (2) 时间离散空间连续信源 (3) 时间连续空间离散信源 (4) 时间连续空间连续信源 简单的表示: 空间离散信源→离散信源 空间连续信源→连续信源

根据信源在1时刻的输出X,中各随机 变量是统计关联性的,可将信源分为: (1)有记忆信源 FX,x(K,x2,,x)=PX4≤x,X2≤x,,X≤Xv) (2)无记忆信源FX.(,x,,xv)=ΠF,(任) (3)平稳信源 序列的统计特性与时间的推移无关 Xw(X,x2,,xw)=FXXm(x,x2,…,xv) (4)非平稳信源 第2章信息的度量 信息理论与编码 4
第2章 信息的度量 信息理论与编码 4 根据信源在 时刻的输出 中各随机 变量是统计关联性的,可将信源分为: (1)有记忆信源 (2)无记忆信源 (3)平稳信源 序列的统计特性与时间的推移无关 (4)非平稳信源 k t k Xt 1 2 1 1 2 1 2 ( , , , ) ( , , , ) t t N N F x x x P X x X x X x X X N t t t N 1 1 2 1 ( , , , ) ( ) t t t N i N X X N X i i F x x x F x 1 1 1 2 1 2 ( , , , ) ( , , , ) t t t t N N F x x x F x x x X X N X X N
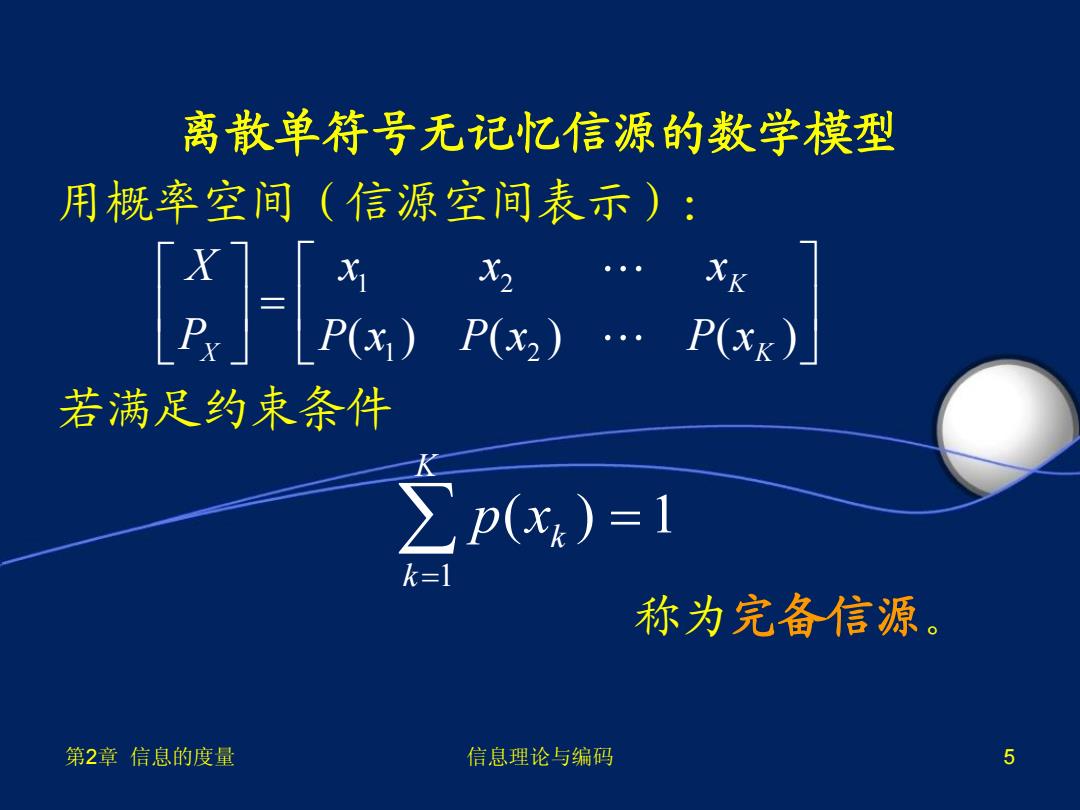
离散单符号无记忆信源的数学模型 用概率空间(信源空间表示): E),/ X2 XK 若满足约束条件 >p(x)=1 k=1 称为完备信源。 第2章信息的度量 信息理论与编码 5
第2章 信息的度量 信息理论与编码 5 离散单符号无记忆信源的数学模型 用概率空间(信源空间表示): 若满足约束条件 称为完备信源。 1 2 1 2 ( ) ( ) ( ) K X K X x x x P P x P x P x 1 ( ) 1 K k k p x