
2二叉树的性质 。性质3:设T是由n个结点构成的二叉树,其中, 叶子结点个数为n,度为2的结点个数 为n2,则有: n0=n2+1
2 二叉树的性质 ● 性质3:设T是由n个结点构成的二叉树,其中, 叶子结点个数为n0, 度为2的结点个数 为n2,则有: n0= n2+1
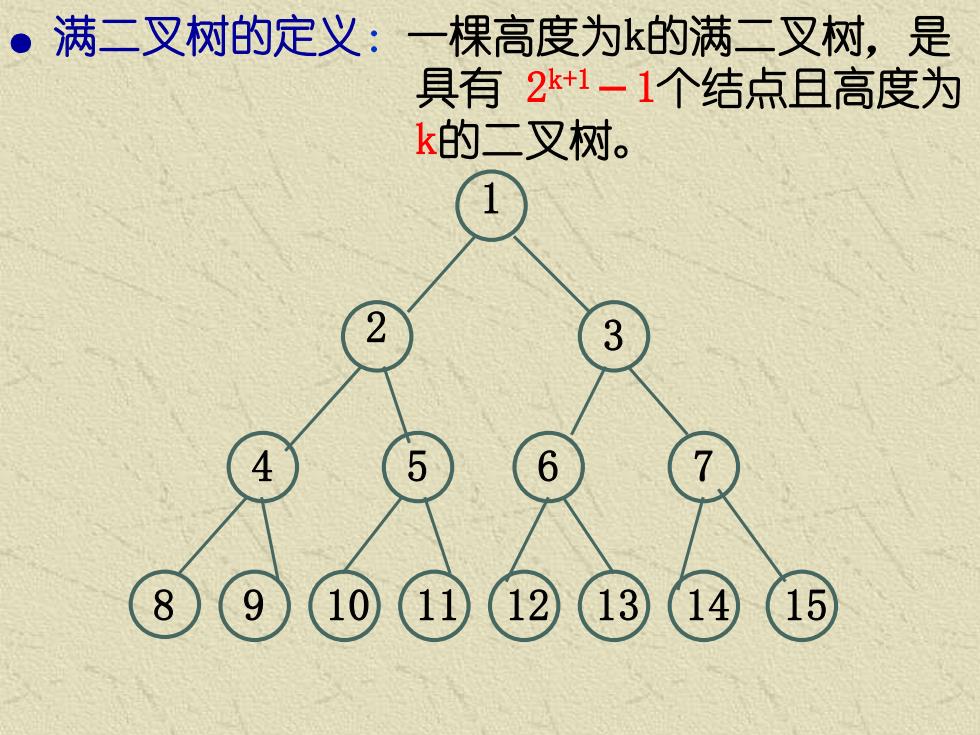
。满二叉树的定义:一棵高度为k的满二叉树,是 具有2+1-1个结点且高度为 k的二叉树。 2 3 4 5 6 8 9 15
● 满二叉树的定义:一棵高度为k的满二叉树,是 具有 2 k+1-1个结点且高度为 k的二叉树。 4 5 6 3 7 2 8 9 10 11 12 13 14 15 1
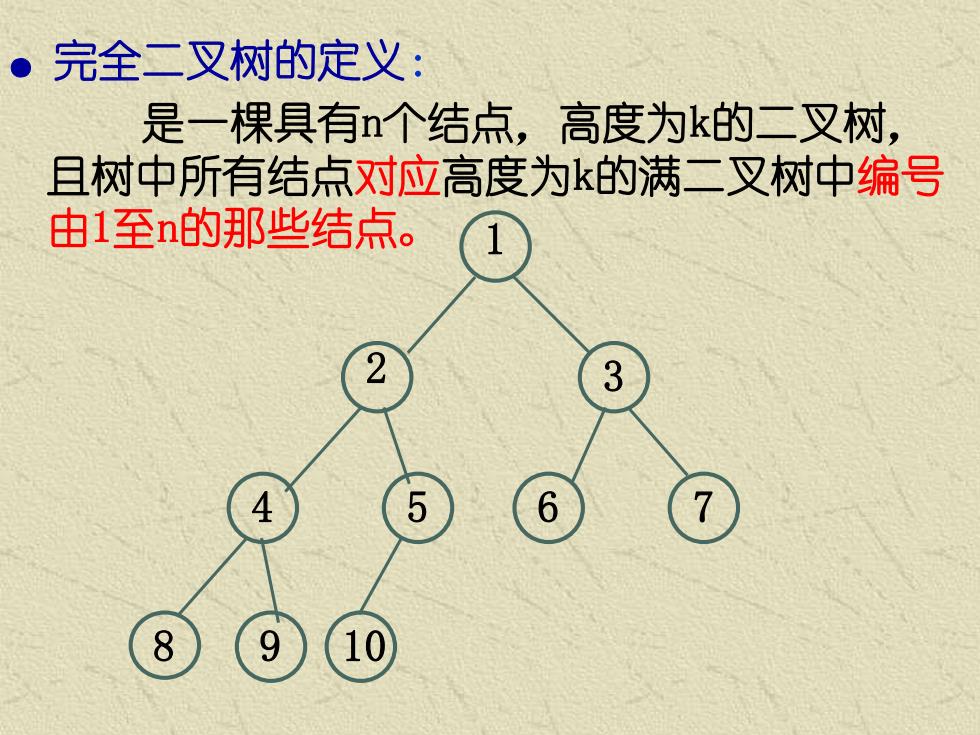
。完全二叉树的定义: 是一棵具有n个结点,高度为k的二叉树, 且树中所有结点对应高度为k的满二叉树中编号 由1至n的那些结点。 3 5 6 8
● 完全二叉树的定义: 是一棵具有n个结点,高度为k的二叉树, 且树中所有结点对应高度为k的满二叉树中编号 由1至n的那些结点。 4 5 6 3 7 2 8 9 10 1

。性质4: 设若将一颗具有n个结点的完全二叉树按层次 次序从1开始编号,则对编号为i(1≤i≤n) 的结点有: ①若i≠1,则编号为1的结点的父结点的编 号为Li/2」 ②若2i≤n,则编号为i的结点的左孩子的 编号为2i,否则无左孩子。 ③若2i+1≤n,则i结点的右孩子结点编号为 21+1,否则i无右孩子
● 性质4: 设若将一颗具有n个结点的完全二叉树按层次 次序从1开始编号,则对编号为i(1≦i ≦ n) 的结点有: ① 若i≠1,则编号为 i 的结点的父结点的编 号为 i/2 」 。 ② 若2i ≦ n,则编号为i的结点的左孩子的 编号为 2i,否则i无左孩子。 ③ 若2i+1 ≦ n,则i结点的右孩子结点编号为 2i+1,否则i无右孩子

。性质5:具有n个结点的完全二叉树的高度是 L1og2n」
● 性质5:具有n个结点的完全二叉树的高度是 log2n 」