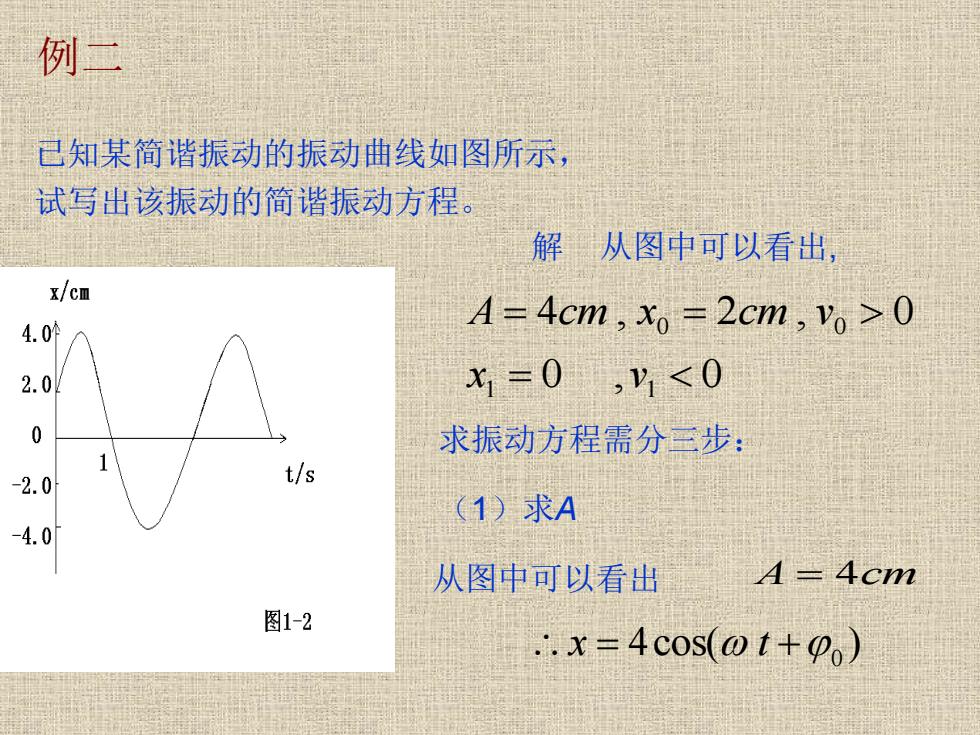
例二 已知某简谐振动的振动曲线如图所示, 试写出该振动的简谐振动方程。 解从图中可以看出, x/cm 4.0f A=4cm,xo=2cm,vo >0 2.0 x1=0,y1<0 求振动方程需分三步: 入 -2.0 t/s (1)求A -4.0 从图中可以看出 A-4cm 图1-2 ..x=4cos(@t+o)
例二 已知某简谐振动的振动曲线如图所示, 试写出该振动的简谐振动方程。 0 , 0 4 , 2 , 0 1 1 0 0 = = = x v A cm x cm v A = 4cm 4cos( ) = +0 x t 解 从图中可以看出, 求振动方程需分三步: 从图中可以看出 (1)求A
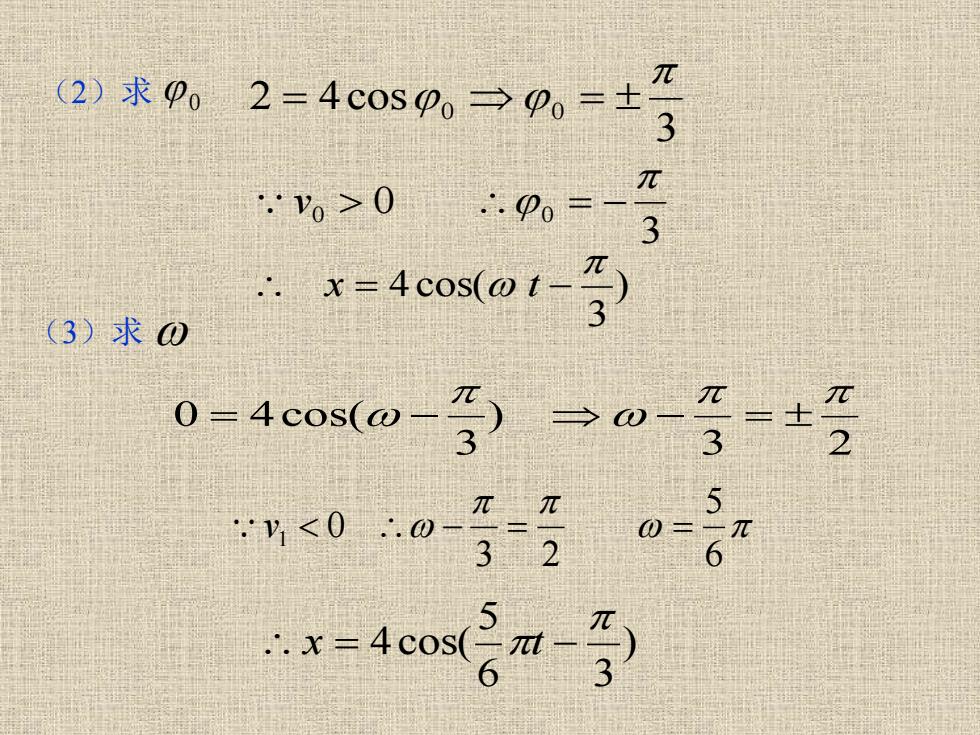
(2)求902=4cosp0→p0=士 3 0>0∴p0= 3 (3)求0 *-4cos(c) 0-4o(0-3=-=± <0w
3 2 ) 3 0 4cos( = − − = 6 5 3 2 v1 0 − = = ) 6 3 5 4cos( x = t − 0 3 0 0 0 v = − 3 2 4cos 0 0 (2)求 = = ) 3 4cos( x = t − (3)求
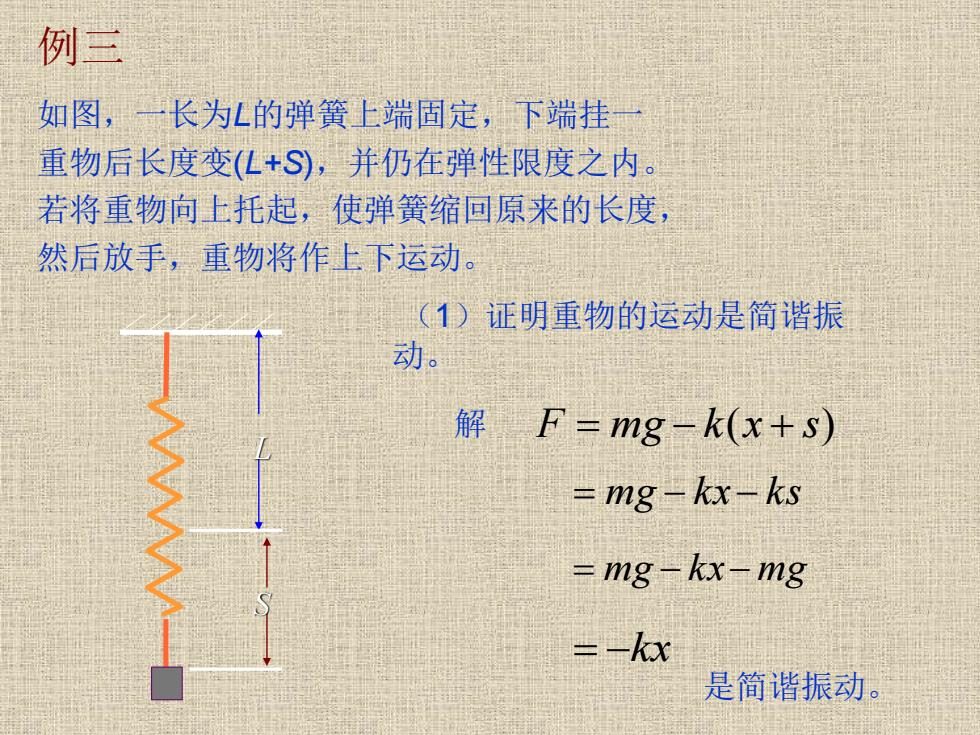
例三 如图,一长为L的弹簧上端固定,下端挂一 重物后长度变(L+S),并仍在弹性限度之内。 若将重物向上托起,使弹簧缩回原来的长度, 然后放手,重物将作上下运动。 (1)证明重物的运动是简谐振 动。 解F=mg-k(x+S) -mg-kx-ks =mg-kx-mg =-kx 是简谐振动
例三 如图,一长为L的弹簧上端固定,下端挂一 重物后长度变(L+S),并仍在弹性限度之内。 若将重物向上托起,使弹簧缩回原来的长度, 然后放手,重物将作上下运动。 F = mg − k(x + s) L S = mg − k x− k s = −kx = mg − k x− mg 是简谐振动。 (1)证明重物的运动是简谐振 动。 解

(2)求A,D,V 解t=0时,x=-S 且静止放手%=0代入A+。 .,A=x0=S o-vm mg =ks 18 mg V- 2元 2s
(2)求 A, , A = x = s 0 s g mg k s m k = = = s g 2 1 2 = = t = x = −s 0 0时, x x S L F mg 2 0 2 0 ( ) v 且 静止放手 v0 = 0 代入 A = x + 解

(3)若以放手时开始计时,求简谐振动方程 解 x=Acos(ot+po) -s cos( 8+po) 将初始条件代入上式:1-0,x。=-s,o=0 -S=SC0sp0→P0=π ..x=s cos(
(3)若以放手时开始计时,求简谐振动方程 cos( ) = +0 x A t − s = s cos0 0 = = cos( t +) s g x s cos( ) = +0 t s g s 将初始条件代入上式: t = 0 , x0 = −s ,v0 = 0 解